- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Движения
Содержание
- 1. Презентация по геометрии на тему Движения
- 2. Движением в геометрии называется отображение плоскости на себя, сохраняющее расстояния.
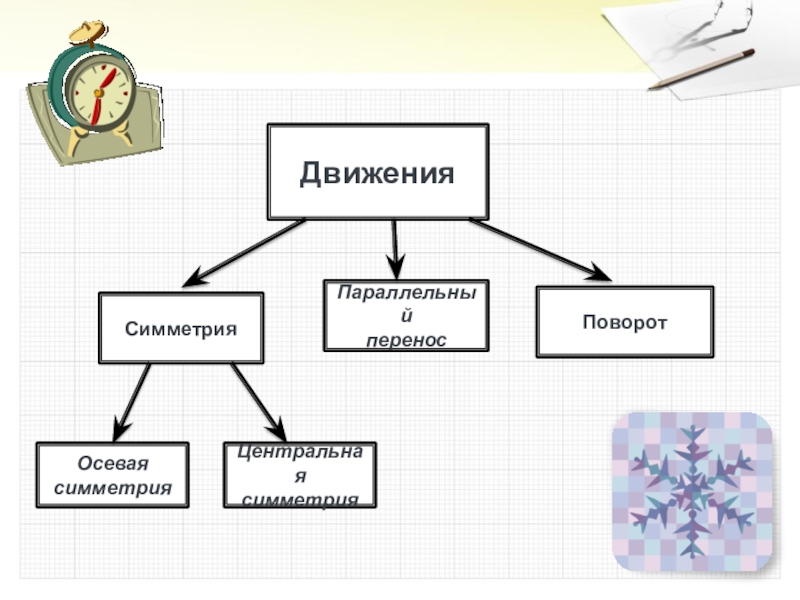
- 3. СимметрияДвиженияПараллельныйпереносПоворотОсеваясимметрияЦентральнаясимметрия
- 4. Виды движенийЦентральная симметрияОсевая симметрия
- 5. Параллельный переносПоворот
- 6. Осевая симметрияОсевая симметрия-это отражение плоскости на себя
- 7. ПостроениеПусть а – ось симметрии.
- 8. Примеры
- 9. Центральная симметрияЦентральная симметрия –это отображение плоскости на
- 10. ПостроениеПусть точка О – центр симметрии. ∆АВС
- 11. Примеры
- 12. Параллельный перенос Параллельный перенос – это отображение
- 13. ПостроениеПусть дан вектор а. ∆АВС произвольный. От
- 14. Примеры
- 15. Поворот Поворот плоскости вокруг точки О на
- 16. ПостроениеПусть О – центр поворота, =90º,
- 17. Примеры
- 18. Симметрия вокруг нас
- 19. Среди архитектурных сооружений фасады зданий и целые композиции обладают центральной и осевой симметрией
- 20. Симметрия окружает нас на улице и дома
- 21. Лицо человека, также как и его тело обладает осью симметрии
- 22. Симметрия в природе
Движением в геометрии называется отображение плоскости на себя, сохраняющее расстояния.
Слайд 6Осевая симметрия
Осевая симметрия-это отражение плоскости на себя ,которое сохраняет расстояние между
точками. Точка М отображается в такую точку М1, что отрезок ММ1 перпендикулярен прямой, а (оси симметрии ) и отрезок МР равен отрезку РМ1.
Слайд 7Построение
Пусть а – ось симметрии.
∆АВС – произвольный. Проведем
перпендикуляр ВР к прямой а. Отложим на прямой ВР отрезок РВ1, равный по длине отрезку ВР. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С 1 симметричен ∆АВС относительно прямой а.
Слайд 9Центральная симметрия
Центральная симметрия –это отображение плоскости на себя , при котором
каждая точка М отображается в такую точку М1,что отрезок ОМ равен отрезку ОМ 1 (точка О - центр симметрии).
Слайд 10Построение
Пусть точка О – центр симметрии. ∆АВС -произвольный. Проведём луч ВО.
Отложим отрезок ОВ1 , равный отрезку ОВ. Точка В1 искомая. Аналогично строим точки А 1 и С1 . ∆А1В1С1 симметричен ∆АВС относительно точки О.
Слайд 12Параллельный
перенос
Параллельный перенос – это отображение плоскости на себя, при котором каждая
точка М отображается в такую точку М1, что вектор ММ1 равен вектору а.
Слайд 13Построение
Пусть дан вектор а. ∆АВС произвольный. От точки В отложим вектор
ВВ1 , равный вектору а. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С1 получен параллельным переносом ∆АВС на вектор а.
Слайд 15Поворот
Поворот плоскости вокруг точки О на угол - это
отображение плоскости на себя , при котором каждая точка М отображается в такую точку М1 , что ОМ=ОМ1 ,< МОМ1= .
Слайд 16Построение
Пусть О – центр поворота, =90º, ∆АВС – произвольный. Проведём
отрезок АВ, от него по часовой стрелке отложим <АОА1 , равный . Отложим отрезок ОА1 равный отрезку ОА. Точка А1 искомая. Аналогично строим точки В1 и С1
Слайд 19Среди архитектурных сооружений фасады зданий и целые композиции обладают центральной и
осевой симметрией