Презентация, доклад по геометрии на тему Движение

Содержание

1. Презентация по геометрии на тему Движение
2. Отображение плоскости на себяЛюбая точка плоскости оказывается
3. Точка плоскости М переходит в точку плоскости
4. Понятие движенияОтображение плоскости на себя, при котором все расстояния сохраняются, называется движением
5. Обобщая, можно сказать, что осевая симметрия является
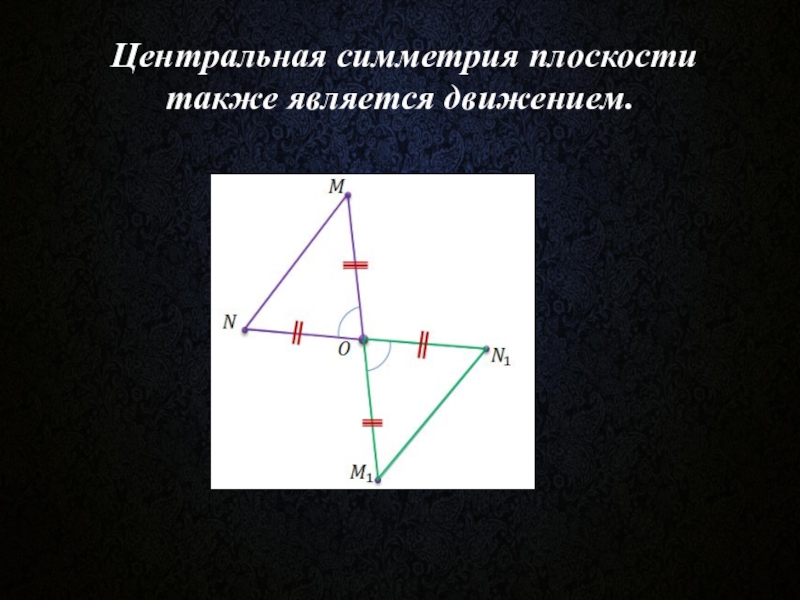
6. Центральная симметрия плоскости также является движением.
7. Теорема. При движении отрезок отображается на отрезок. СледствиеПри движении треугольник отображается на равный ему треугольник.
8. фигура Ф равна фигуре Ф1, если фигуру
9. ПРИ НАЛОЖЕНИИ РАЗЛИЧНЫЕ ТОЧКИ ОТОБРАЖАЮТСЯ В
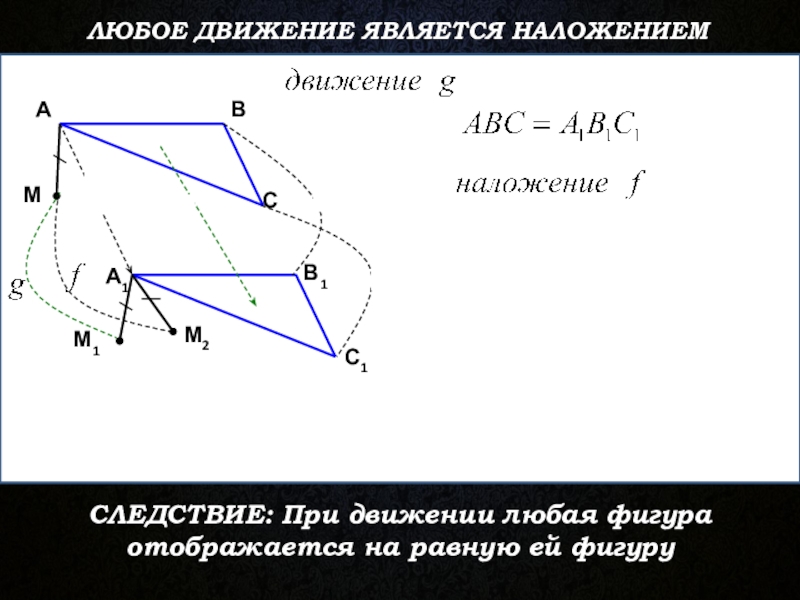
10. ЛЮБОЕ ДВИЖЕНИЕ ЯВЛЯЕТСЯ НАЛОЖЕНИЕММСАВС1А1В1М1М2СЛЕДСТВИЕ: При движении любая фигура отображается на равную ей фигуру

Отображение плоскости на себяЛюбая точка плоскости оказывается сопоставленной некоторой точке.Осевая симметрия – это такой тип симметрии, при которой каждой точке плоскости, например в точке М, по определенному закону ставится в соответствие другая точка той же плоскости.Осевая

Главная
Геометрия
Презентация по геометрии на тему Движение

Слайд 1Движение

Слайд 2Отображение плоскости на себя
Любая точка плоскости оказывается сопоставленной некоторой точке.
Осевая симметрия

– это такой тип симметрии, при которой каждой точке плоскости, например в точке М, по определенному закону ставится в соответствие другая точка той же плоскости.

Осевая симметрия является частным случаем так называемого отображения плоскости на себя.

Отображение плоскости на себяЛюбая точка плоскости оказывается сопоставленной некоторой точке.Осевая симметрия – это такой тип симметрии, при

Слайд 3Точка плоскости М переходит в точку плоскости другую М1 по следующему закону

:
1. проводится прямая МО
2. эта прямая продолжается и на ней откладывается отрезок ОМ1=ОМ, получаем точку М1
М1 ставится в соответствие точке М.

Другим частным случаем отображения плоскости на саму себя является центральная симметрия.

Точка плоскости М переходит в точку плоскости другую М1 по следующему закону :1. проводится прямая МО2. эта прямая

Слайд 4Понятие движения
Отображение плоскости на себя, при котором все расстояния сохраняются, называется движением

Слайд 5Обобщая, можно сказать, что осевая симметрия является отображением, которое сохраняет расстояние

между точками. Любое отображение, обладающее этим свойством, называется движением (перемещением).

Почему такое отображение называется движением? Если рассмотреть осевую симметрию, то она представляет собой поворот плоскости в пространстве на 180º вокруг оси А.

Обобщая, можно сказать, что осевая симметрия является отображением, которое сохраняет расстояние между точками. Любое отображение, обладающее этим

Слайд 6 Центральная симметрия плоскости также является движением.

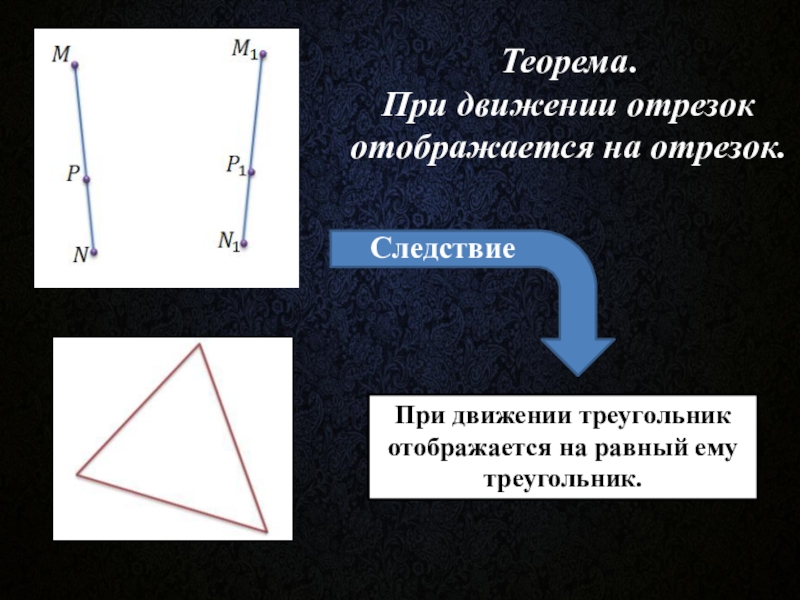
Слайд 7Теорема.
При движении отрезок отображается на отрезок.

Следствие
При движении треугольник отображается на

равный ему треугольник.

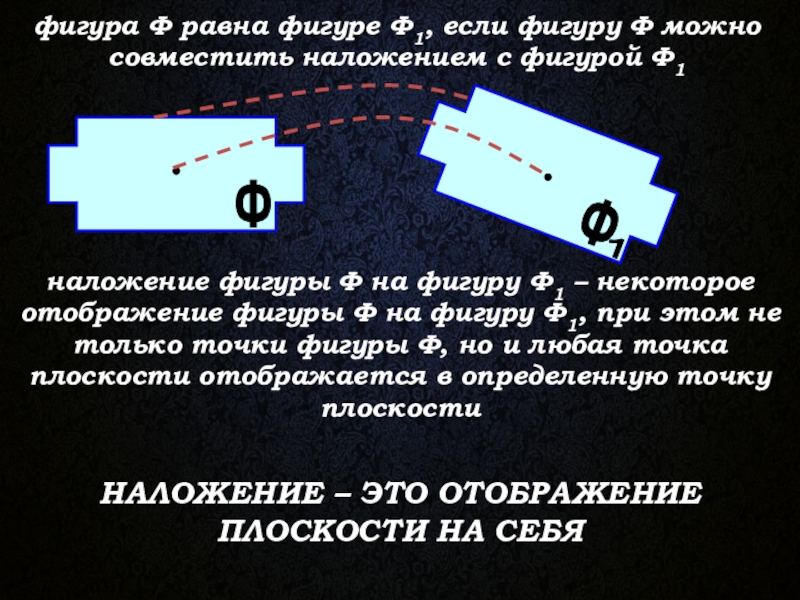
Слайд 8фигура Ф равна фигуре Ф1, если фигуру Ф можно совместить наложением

с фигурой Ф1

наложение фигуры Ф на фигуру Ф1 – некоторое отображение фигуры Ф на фигуру Ф1, при этом не только точки фигуры Ф, но и любая точка плоскости отображается в определенную точку плоскости

НАЛОЖЕНИЕ – ЭТО ОТОБРАЖЕНИЕ ПЛОСКОСТИ НА СЕБЯ

фигура Ф равна фигуре Ф1, если фигуру Ф можно совместить наложением с фигурой Ф1наложение фигуры Ф на

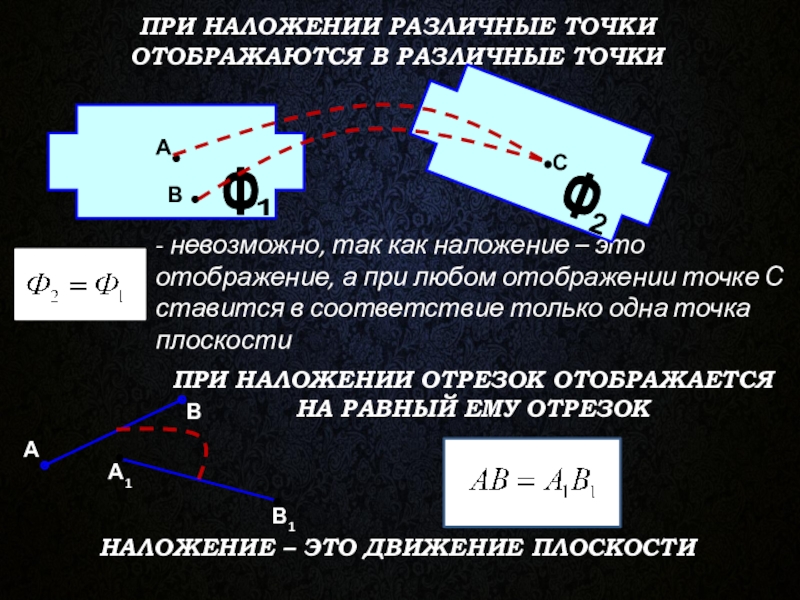
Слайд 9ПРИ НАЛОЖЕНИИ РАЗЛИЧНЫЕ ТОЧКИ ОТОБРАЖАЮТСЯ В РАЗЛИЧНЫЕ ТОЧКИ
- невозможно, так как

наложение – это отображение, а при любом отображении точке С ставится в соответствие только одна точка плоскости

ПРИ НАЛОЖЕНИИ ОТРЕЗОК ОТОБРАЖАЕТСЯ НА РАВНЫЙ ЕМУ ОТРЕЗОК

А1

В1

НАЛОЖЕНИЕ – ЭТО ДВИЖЕНИЕ ПЛОСКОСТИ

ПРИ НАЛОЖЕНИИ РАЗЛИЧНЫЕ ТОЧКИ ОТОБРАЖАЮТСЯ В РАЗЛИЧНЫЕ ТОЧКИ- невозможно, так как наложение – это отображение, а

Слайд 10ЛЮБОЕ ДВИЖЕНИЕ ЯВЛЯЕТСЯ НАЛОЖЕНИЕМ
М
С
А
В
С1
А1
В1
М1
М2
СЛЕДСТВИЕ: При движении любая фигура отображается на равную

ей фигуру

Скачать презентацию

Презентация, доклад по геометрии на тему Движение

Содержание

Слайд 1Движение

Слайд 2Отображение плоскости на себя
Любая точка плоскости оказывается сопоставленной некоторой точке.
Осевая симметрия

Слайд 3Точка плоскости М переходит в точку плоскости другую М1 по следующему закону

Слайд 4Понятие движения
Отображение плоскости на себя, при котором все расстояния сохраняются, называется движением

Слайд 5Обобщая, можно сказать, что осевая симметрия является отображением, которое сохраняет расстояние

Слайд 6 Центральная симметрия плоскости также является движением.

Слайд 7Теорема.
При движении отрезок отображается на отрезок.

Следствие
При движении треугольник отображается на

Слайд 8фигура Ф равна фигуре Ф1, если фигуру Ф можно совместить наложением

Слайд 9ПРИ НАЛОЖЕНИИ РАЗЛИЧНЫЕ ТОЧКИ ОТОБРАЖАЮТСЯ В РАЗЛИЧНЫЕ ТОЧКИ
- невозможно, так как

Слайд 10ЛЮБОЕ ДВИЖЕНИЕ ЯВЛЯЕТСЯ НАЛОЖЕНИЕМ
М
С
А
В
С1
А1
В1
М1
М2
СЛЕДСТВИЕ: При движении любая фигура отображается на равную

Что такое shareslide.ru?

Обратная связь

Презентация, доклад по геометрии на тему Движение

Содержание

Слайд 1Движение

Слайд 2Отображение плоскости на себяЛюбая точка плоскости оказывается сопоставленной некоторой точке.Осевая симметрия

Слайд 3Точка плоскости М переходит в точку плоскости другую М1 по следующему закону

Слайд 4Понятие движенияОтображение плоскости на себя, при котором все расстояния сохраняются, называется движением

Слайд 5Обобщая, можно сказать, что осевая симметрия является отображением, которое сохраняет расстояние

Слайд 6 Центральная симметрия плоскости также является движением.

Слайд 7Теорема. При движении отрезок отображается на отрезок. СледствиеПри движении треугольник отображается на

Слайд 8фигура Ф равна фигуре Ф1, если фигуру Ф можно совместить наложением

Слайд 9ПРИ НАЛОЖЕНИИ РАЗЛИЧНЫЕ ТОЧКИ ОТОБРАЖАЮТСЯ В РАЗЛИЧНЫЕ ТОЧКИ- невозможно, так как

Слайд 10ЛЮБОЕ ДВИЖЕНИЕ ЯВЛЯЕТСЯ НАЛОЖЕНИЕММСАВС1А1В1М1М2СЛЕДСТВИЕ: При движении любая фигура отображается на равную

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 2Отображение плоскости на себя
Любая точка плоскости оказывается сопоставленной некоторой точке.
Осевая симметрия

Слайд 4Понятие движения
Отображение плоскости на себя, при котором все расстояния сохраняются, называется движением

Слайд 7Теорема.
При движении отрезок отображается на отрезок.

Следствие
При движении треугольник отображается на

Слайд 9ПРИ НАЛОЖЕНИИ РАЗЛИЧНЫЕ ТОЧКИ ОТОБРАЖАЮТСЯ В РАЗЛИЧНЫЕ ТОЧКИ
- невозможно, так как

Слайд 10ЛЮБОЕ ДВИЖЕНИЕ ЯВЛЯЕТСЯ НАЛОЖЕНИЕМ
М
С
А
В
С1
А1
В1
М1
М2
СЛЕДСТВИЕ: При движении любая фигура отображается на равную