- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Длина окружности и площадь круга (9 класс)
Содержание
- 1. Презентация по геометрии на тему Длина окружности и площадь круга (9 класс)
- 2. Подготовить учащихся к контрольной работе.Совершенствовать навыки решения задач.Геометрия приближает разум к истине.Платон.Цели урока:
- 3. Проверочный тест 1вариант1. Четырехугольник является правильным, если:а)
- 4. Проверочный тест 2 вариант1. Если в четырехугольнике
- 5. Тест с последующей самопроверкой. 1.Один из внутренних
- 6. Вопросы: Чему равна сторона правильного ∆, описанного
- 7. Вопросы: Чем являются радиусы ОА и ОВ,
- 8. Самостоятельная работа1вариант1.Найдите площадь круга и длину ограничивающей
- 9. Самостоятельная работа2. Вычислите длину дуги окружности с
- 10. 1вариант3. Периметр правильного треугольника , вписанного в
- 11. Самостоятельная работа2вариант1.Найдите площадь круга и длину ограничивающей
- 12. 2 вариант3. Периметр квадрата , описанного около
- 13. Выбери вариант соответствующий твоим ощущениям после сегодняшнего
Слайд 2
Подготовить учащихся к контрольной работе.
Совершенствовать навыки решения задач.
Геометрия приближает разум к
Платон.
Цели урока:
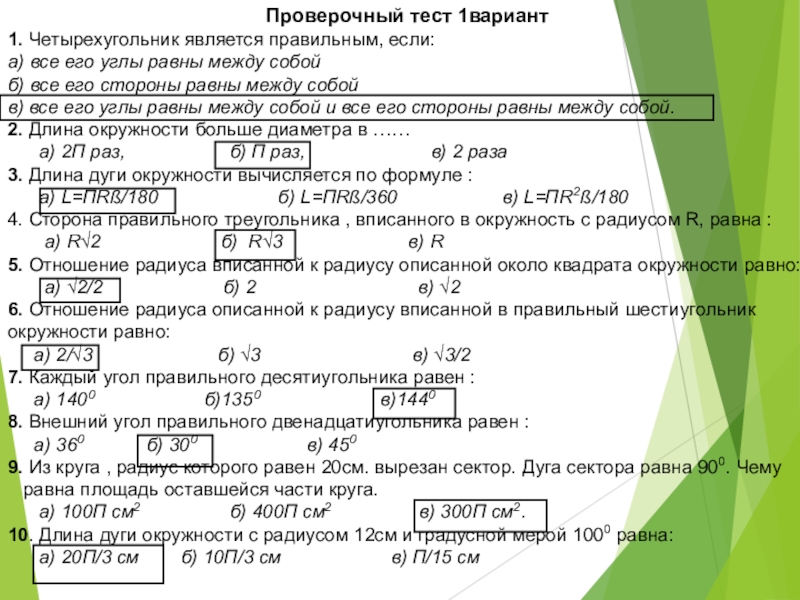
Слайд 3Проверочный тест 1вариант
1. Четырехугольник является правильным, если:
а) все его углы равны
б) все его стороны равны между собой
в) все его углы равны между собой и все его стороны равны между собой.
2. Длина окружности больше диаметра в ……
а) 2П раз, б) П раз, в) 2 раза
3. Длина дуги окружности вычисляется по формуле :
а) L=ПRß/180 б) L=ПRß/360 в) L=ПR2ß/180
4. Сторона правильного треугольника , вписанного в окружность с радиусом R, равна :
а) R√2 б) R√3 в) R
5. Отношение радиуса вписанной к радиусу описанной около квадрата окружности равно:
а) √2/2 б) 2 в) √2
6. Отношение радиуса описанной к радиусу вписанной в правильный шестиугольник окружности равно:
а) 2/√3 б) √3 в) √3/2
7. Каждый угол правильного десятиугольника равен :
а) 1400 б)1350 в)1440
8. Внешний угол правильного двенадцатиугольника равен :
а) 360 б) 300 в) 450
9. Из круга , радиус которого равен 20см. вырезан сектор. Дуга сектора равна 900. Чему
равна площадь оставшейся части круга.
а) 100П см2 б) 400П см2 в) 300П см2.
10. Длина дуги окружности с радиусом 12см и градусной мерой 1000 равна:
а) 20П/3 cм б) 10П/3 см в) П/15 см
Слайд 4Проверочный тест 2 вариант
1. Если в четырехугольнике все стороны равны, то
а) всегда является правильным
б) может быть правильным
в) никогда не является правильным
2. Длина окружности больше радиуса в :
а) 2П раз, б) П раз в) 2 раза
3. Площадь кругового сектора вычисляется по формуле:
а) L=ПR2ß/180 б) L=ПRß/180 в) L=ПR2ß/360
4. Сторона правильного четырехугольника, вписанного в окружность с радиусом R, равна:
а) R б) R√2 в) R√3
5. Отношение радиуса описанной к радиусу вписанной в квадрат окружности равно:
а) 2 б) √2/2 в) √2
6. Отношение радиуса вписанной к радиусу описанной около правильного шестиугольника окружности равно:
а) √3 б) √3/2 в) 2/√3
7. Каждый угол правильного восьмиугольника равен:
а) 1350 б) 1440 в) 1400
8. Внешний угол правильного двадцатиугольника равен:
а) 200 б) 22,50 в) 180
9. Из круга, радиус которого равен 30см, вырезан сектор. Дуга сектора равна 600. Чему равна площадь оставшейся части круга.
а) 150П см2 б) 750П см2 в) 900П см2
10. Длина дуги окружности с радиусом 6см и градусной мерой 1350 равна:
а) 9П/2 см б) 9П см в) 9П/4 см
Слайд 5Тест с последующей самопроверкой.
1.Один из внутренних углов правильного n-угольника равен
Найдите число сторон многоугольника.
а) 9 б) 14 в) 12 г) 15
2. Периметр правильного треугольника равен 12 3 см.
Найдите радиус вписанной окружности
а) 2см б) 4см в) 4/ √3 г) 2/√ 3
3. Около квадрата описана окружность и в квадрат вписана окружность .
Найдите отношение радиуса описанной окружности к радиусу вписанной
окружности .
а) 1/ √2 б) √2 в) 2 г) 1/2
4. Сторона правильного шестиугольника равна 2м . На сколько площадь
описанного круга больше площади вписанного круга.
а) 3√3 б) 3√ 3/ 4 в) 6√3 г) 3√3 / 2
5. Рис. Площадь полуокружности с центром в точке О равна 8П .
Найдите площадь заштрихованной фигуры.
а) 16П б) 8П в) 4П г) 32П
6. В окружности вписаны квадрат и правильный треугольник. Периметр
треугольника равен 30см, периметр квадрата равен .
а) 40√ 6/3 б) 10 √6 /3 в) 40 /3 г) 20 √6 /3
Ответы: 1-(в), 2-(а), 3- (б), 4- (г), 5- (б), 6- (а).
Слайд 6Вопросы:
Чему равна сторона правильного ∆, описанного около круга радиуса r
Выразите площадь треугольника через r ?
Чему равна площадь круга радиуса r?
Чему равна разность площадей ∆ и вписанную в него круга?
Найдите радиус r.
Задача1: Площадь правильного треугольника больше площади вписанного в него круга на 27√3 – 9П
Решение: Пусть радиус вписанного круга равен r. Тогда площадь S=Пr².
Сторона правильного ∆ , описанного около круга.
Тогда S∆=½∙а3∙а3∙sin60°= ½∙2√3r∙√3/2=3∙√3∙r²
Тогда S∆ - Sкр=3∙√3∙r²-Пr²=r²(3√3 - П)
По условию задачи S∆ - Sкр=27∙√3 – 9П=9(3√3 - П), тогда
r²(3√3 - П)=9(3√3 – П), r=3
Ответ: r=3
Слайд 7Вопросы:
Чем являются радиусы ОА и ОВ, кругового сектора с дугой
Постройте ∆ОСО1 . Какие элементы в данном ∆ известны?
Как найти S незаштрихованной фигуры?
Как найти S кругового сектора с дугой АЕВ?
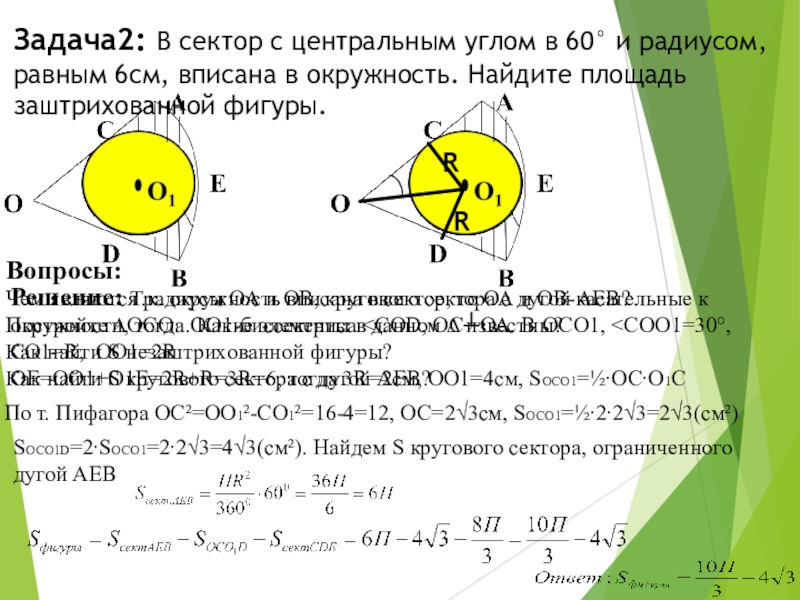
Задача2: В сектор с центральным углом в 60° и радиусом, равным 6см, вписана в окружность. Найдите площадь заштрихованной фигуры.
Решение: Т.к. окружность вписана в сектор, то ОА и ОВ-касательные к окружности, тогда ОО1-биссектриса <СОD, ОС┴ОА. В ОСО1, <СОО1=30°, СО1=R, ОО1=2R
ОЕ=ОО1+О1Е=2R+R=3R=6, тогда 3R=2см, ОО1=4см, SОСО1=½∙ОС∙О1С
По т. Пифагора ОС²=ОО1²-СО1²=16-4=12, ОС=2√3см, SОСО1=½∙2∙2√3=2√3(см²)
R
R
SОСО1D=2∙SОСО1=2∙2√3=4√3(cм²). Найдем S кругового сектора, ограниченного дугой АЕВ
Слайд 8Самостоятельная работа
1вариант
1.Найдите площадь круга и длину ограничивающей его окружности , если
2. Вычислите длину дуги окружности с радиусом 4см, если ее градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора.
3. Периметр правильного треугольника , вписанного в окружность , равен 6√3 дм. Найдите периметр правильного шестиугольника , описанного около той же окружности .
4*Рис. Найдите площадь
заштрихованной на рис. фигуры, если ВС=4, < ВАС=300, О – центр окружности.
2вариант
1.Найдите площадь круга и длину ограничивающей его окружности , если сторона квадрата , описанного около него ,равна 6см.
2. Вычислите длину дуги окружности с радиусом 10см, если ее градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора.
3. Периметр квадрата , описанного около окружности , равен 16дм. Найдите периметр правильного пятиугольника , вписанного в эту окружность .
4*Рис. Найдите площадь заштрихованной на рис. фигуры, если О - центр окружности с диаметром 10√2.
Ответы: 1. S=25Псм², С=10Псм
2. С=4Псм S=16П/3 cм²
3. 8√3
4. 16П-8√3
Ответы: 1. S=9Псм², С=6Псм
2. С=25П/3см S=125П/3 cм²
3. 20sin36°
4. 50П-50
Слайд 9Самостоятельная работа
2. Вычислите длину дуги окружности с радиусом 4см, если ее
Решение:
Площадь круга находится по формуле:
Длина ограничивающей круг окружности
Решение: R=4cм.
1 вариант
1. Найдите площадь круга и длину ограничивающей его окружности , если сторона квадрата , правильного ∆, вписанного в него, равна 5√3 см.
Радиус описанной окружности= а∙√3/3= 5 √3 ∙√3/3=5
Слайд 101вариант
3. Периметр правильного треугольника , вписанного в окружность , равен 6√3
Решение:
Решение:
сторона ∆ 6√3/3=2√3
АВ²=АС²-ВС²=64-16, АВ=4√3
Sкруга=ПR², S=4²П=16П
Искомая площадь тогда S=16П-8√3
R=2√3/√3=2
4*Рис. Найдите площадь заштрихованной на рис. фигуры, если ВС=4, < ВАС=300, О – центр окружности
угол В=90, т.к. опирается на диаметр АС, треугольник АВС прямоугольный , ВС лежит напротив <30° ВС= 1/2 АВ. АВ = 2 ∙ ВС = 2∙ 4 =8, R= АВ/2=4
S∆=½∙АВ∙ВС=½∙4√3∙4=8√3
искомая S= Sкруга- S треугольника=16П-8√3
Слайд 11Самостоятельная работа
2вариант
1.Найдите площадь круга и длину ограничивающей его окружности , если
2. Вычислите длину дуги окружности с радиусом 10см, если ее градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора.
Решение: Если квадрат описан около круга, значит круг вписан. Найдем радиус вписанной в квадрат окружности
Площадь круга находится по формуле:
Длина ограничивающей круг окружности
Решение: R=10cм.
Слайд 122 вариант
3. Периметр квадрата , описанного около окружности , равен 16дм.
4*Рис. Найдите площадь заштрихованной на рис. фигуры, если О - центр окружности с диаметром 10√2.
Решение:
Решение:
сторона квадрата = 4дм т.к 16/4=4
радиус вписанной окружности в кв-т равен 2 так как диаметр равен стороне квадрата..
формула для стороны правильного n-угольника, вписанного в окружность:
a = 2R*sin (180/n)
треугольник прямоугольный угол В=90 - опирается на диаметр, АВ=ВС
АС² = АВ²+ ВС² 200 = 2 ∙АВ² АВ =ВС=10
S∆=½∙АВ∙ВС=50
Sокружности=ПR², R=D/2=АС/2=5√2, S=П(5√2)²=50П
Искомая площадь тогда S=50П-50
Слайд 13Выбери вариант соответствующий твоим ощущениям после сегодняшнего занятия. 1. Я все
Рефлексия