- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Аксиомы планиметрии и стереометрии (10 класс)
Содержание
- 1. Презентация по геометрии на тему: Аксиомы планиметрии и стереометрии (10 класс)
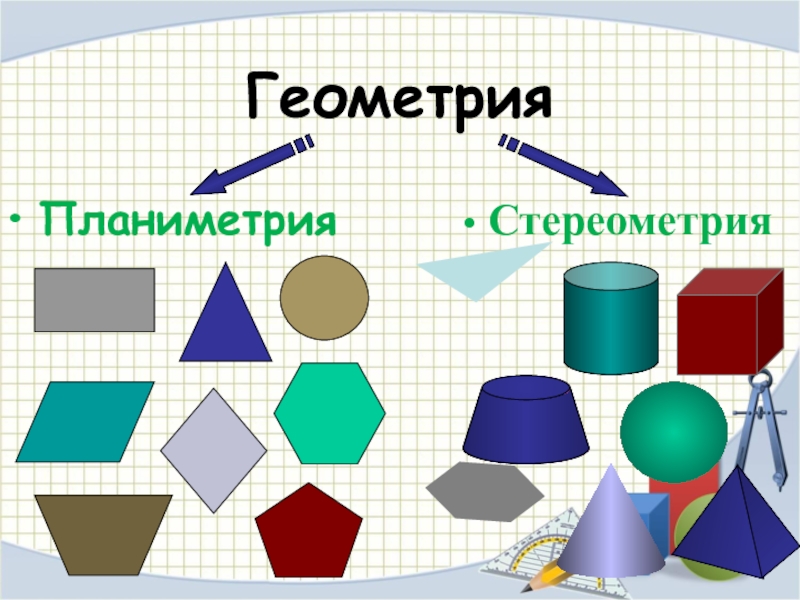
- 2. Геометрия Планиметрия Стереометрия
- 3. Планиметрия
- 4. Точка и прямаяТочка — абстрактный объект в
- 5. Треугольник Треугольник — простейший многоугольник, имеющий 3
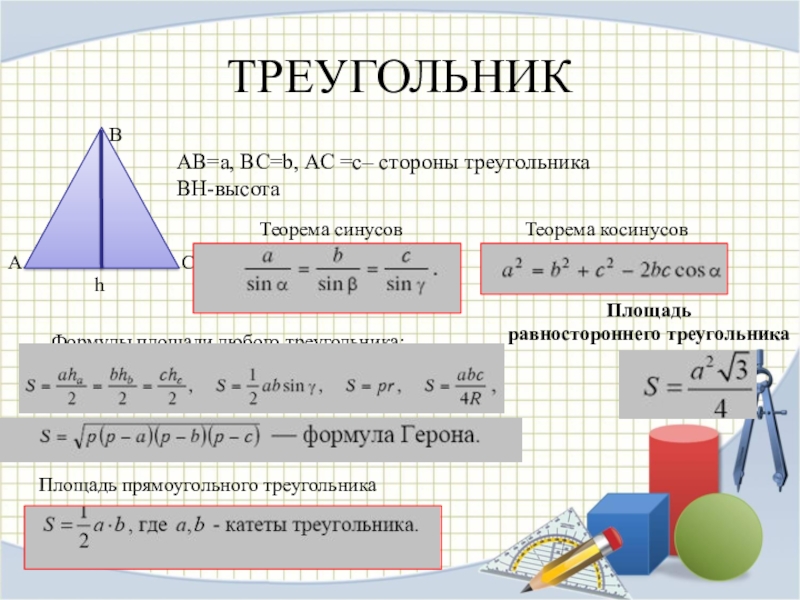
- 6. ТРЕУГОЛЬНИКhАВ=a, ВС=b, АС =c– стороны треугольникаBH-высотаТеорема синусовТеорема косинусовФормулы площади любого треугольника:Площадь прямоугольного треугольникаПлощадь равностороннего треугольника
- 7. Параллелограмм Параллелограмм (от греч. parallelos —
- 8. Свойства параллелограмма:Противоположные стороны параллелограмма равны.Противоположные углы параллелограмма
- 9. Трапеция Трапеция — геометрическая фигура, четырехугольник,
- 10. ТРАПЕЦИЯСвойства сторон:Свойства средней линии: Площадь:
- 11. Окружность Окружность — замкнутая плоская кривая,
- 12. ОКРУЖНОСТЬУглы, вписанные в окружность:Свойства хорд: Свойства секущих:
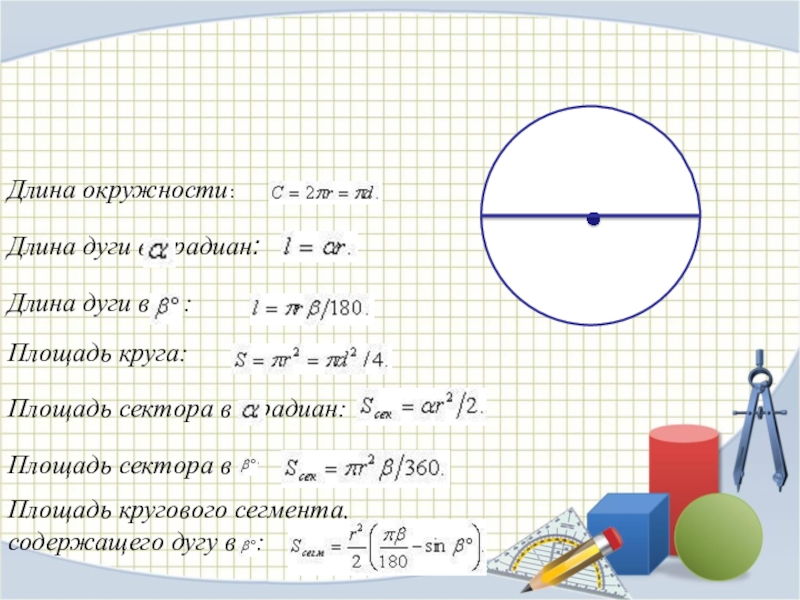
- 13. Длина окружности:Длина дуги в радиан:
- 14. Многоугольник Многоугольник — это геометрическая фигура,
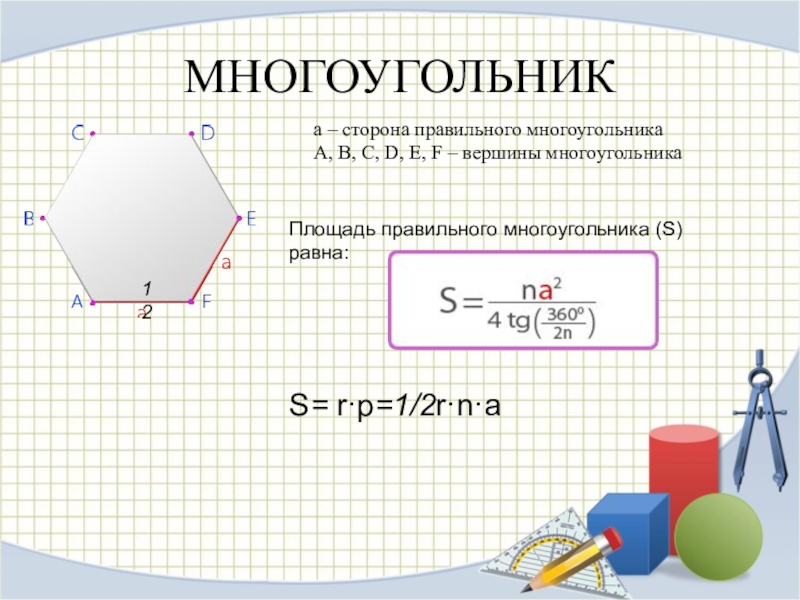
- 15. МНОГОУГОЛЬНИКa – сторона правильного многоугольникаA, B, C,
- 16. Стереометрия - раздел геометрии, в котором изучаются свойства фигур в пространстве.
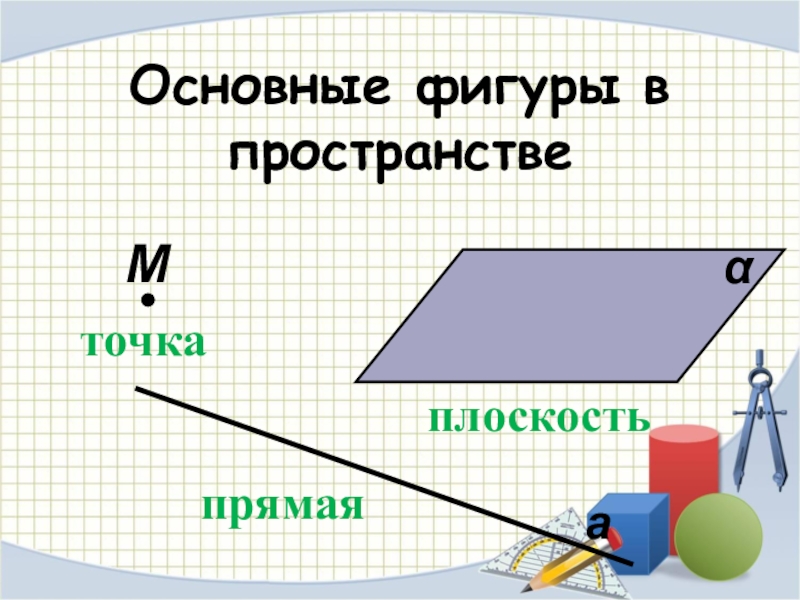
- 17. Основные фигуры в пространстветочкапрямаяплоскостьМαа
- 18. Аксиомы стереометрии и их следствия Аксиома 1. Аксиома 2. Аксиома 3. Следствие 1. Следствие 2.
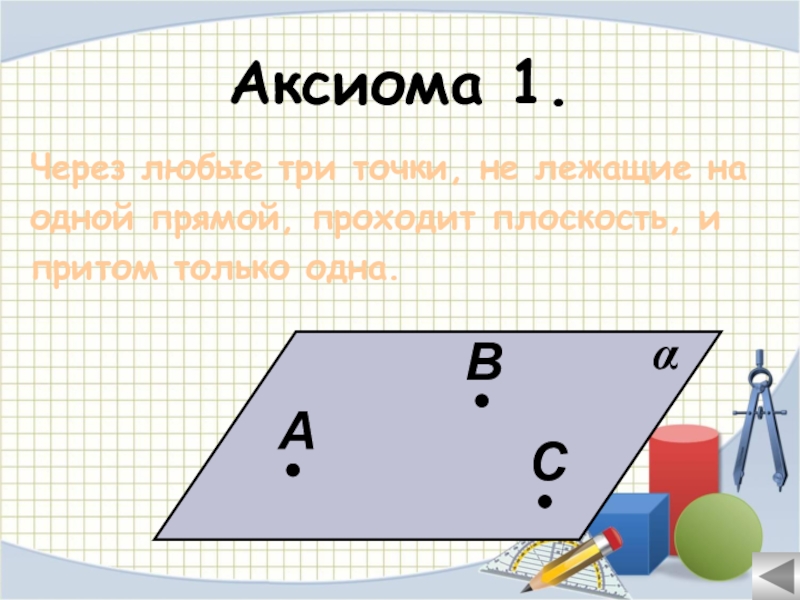
- 19. Аксиома 1.Через любые три точки, не лежащие наодной прямой, проходит плоскость, и притом только одна.αАВС
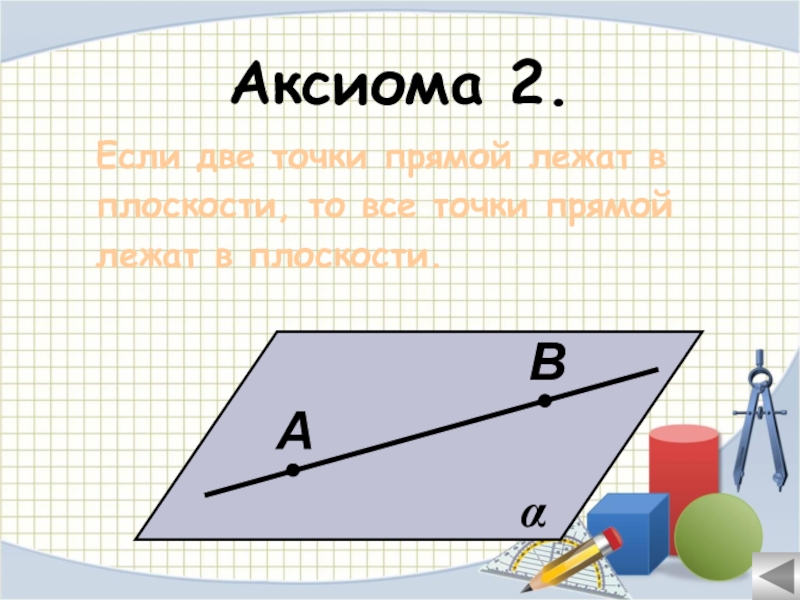
- 20. Аксиома 2.Если две точки прямой лежат в плоскости, то все точки прямойлежат в плоскости.αАВ
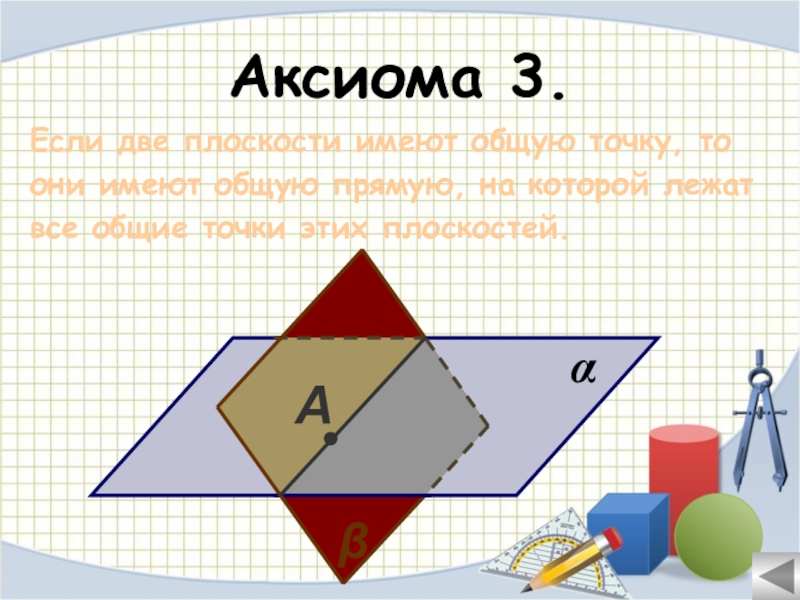
- 21. Аксиома 3.Если две плоскости имеют общую точку,
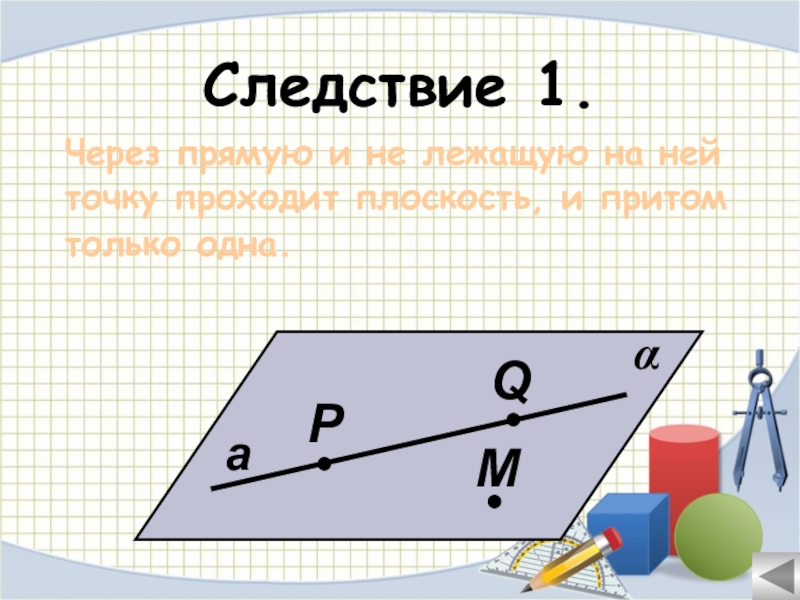
- 22. Следствие 1.Через прямую и не лежащую на нейточку проходит плоскость, и притом только одна.αPМаQ
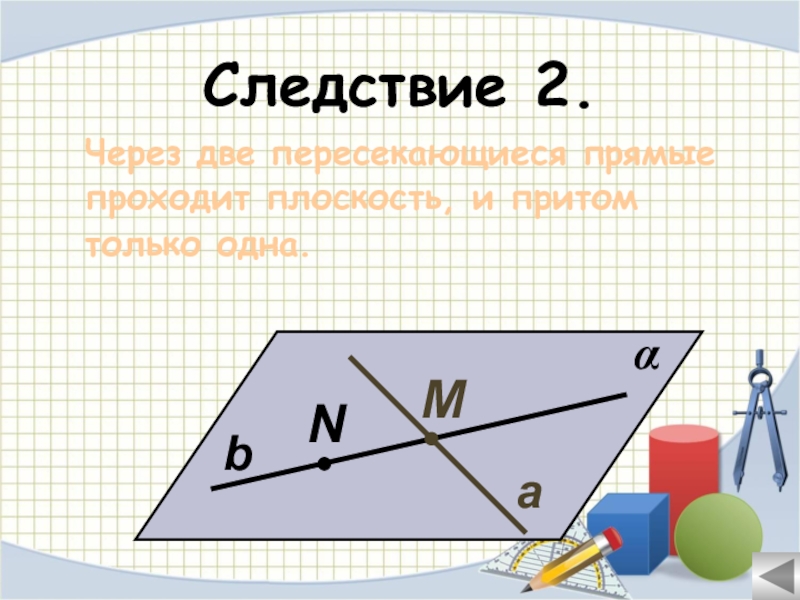
- 23. Следствие 2.Через две пересекающиеся прямые проходит плоскость, и притом только одна.αNМba
Геометрия Планиметрия Стереометрия
Слайд 3
Планиметрия
Планиметрия — раздел геометрии, изучающий двумерные
(одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Фигуры, изучаемые планиметрией:
Точка
Прямая
Параллелограмм (частные случаи Квадрат, Прямоугольник, Ромб)
Трапеция
Окружность
Треугольник
Многоугольник
Точка
Прямая
Параллелограмм (частные случаи Квадрат, Прямоугольник, Ромб)
Трапеция
Окружность
Треугольник
Многоугольник
Слайд 4Точка и прямая
Точка — абстрактный объект в пространстве, обладающий координатами, но
не имеющий размеров, массы, направленности и каких-либо других геометрических или физических характеристик. Одно из фундаментальных понятий в математике и физике.
Прямая. Прямая линия — одно из основных понятий геометрии. При систематической изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Прямая. Прямая линия — одно из основных понятий геометрии. При систематической изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Слайд 5Треугольник
Треугольник — простейший многоугольник, имеющий 3 вершины и 3 стороны;
часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.
Слайд 6ТРЕУГОЛЬНИК
h
АВ=a, ВС=b, АС =c– стороны треугольника
BH-высота
Теорема синусов
Теорема косинусов
Формулы площади любого треугольника:
Площадь
прямоугольного треугольника
Площадь
равностороннего треугольника
Слайд 7Параллелограмм
Параллелограмм (от греч. parallelos — параллельный и gramme —
линия) — это четырехугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Частным случаем параллелограмма (являются прямоугольник и ромб.
Слайд 8Свойства параллелограмма:
Противоположные стороны параллелограмма равны.
Противоположные углы параллелограмма равны.
Диагонали параллелограмма в точке пересечения
делятся пополам.
Формула площади параллелограмма:
Формула периметра параллелограмма:
Слайд 9Трапеция
Трапеция — геометрическая фигура, четырехугольник, у которого только две
противолежащие стороны параллельны. Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми сторонами . Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
С
D
А
В
Слайд 11Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково
удалены от данной точки (центра окружности), лежащей в той же плоскости, что и кривая.
Слайд 13Длина окружности:
Длина дуги в радиан:
Длина дуги в
:
Площадь круга:
Площадь сектора в радиан:
Площадь сектора в :
Площадь кругового сегмента,
содержащего дугу в :
Слайд 14Многоугольник
Многоугольник — это геометрическая фигура, обычно определяется как замкнутая
ломаная без самопересечений, однако иногда самопересечения допускаются. Иногда многоугольник определяется как замкнутая область плоскости ограниченная замкнутой ломаной без самопересечений. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника. Вершины многоугольника называются соседними, если они являются концами одной из его сторон. Отрезки, соединяющие не соседние вершины
многоугольника, называются диагоналями.
многоугольника, называются диагоналями.
Слайд 15МНОГОУГОЛЬНИК
a – сторона правильного многоугольника
A, B, C, D, E, F –
вершины многоугольника
Площадь правильного многоугольника (S) равна:
S= r·p=1/2r·n·a
Слайд 18Аксиомы стереометрии
и их следствия
Аксиома 1.
Аксиома 2.
Аксиома 3.
Следствие
1.
Следствие 2.
Следствие 2.
Слайд 19Аксиома 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость,
и
притом только одна.
притом только одна.
α
А
В
С
Слайд 21Аксиома 3.
Если две плоскости имеют общую точку, то
они имеют общую
прямую, на которой лежат
все общие точки этих плоскостей.
все общие точки этих плоскостей.
α
А
Слайд 22Следствие 1.
Через прямую и не лежащую на ней
точку проходит плоскость, и
притом
только одна.
только одна.
α
P
М
а
Q
