- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Аксиомы стереометрии (10 класс)
Содержание
- 1. Презентация по геометрии на тему Аксиомы стереометрии (10 класс)
- 2. Слайд 2
- 3. Стереометрия – это раздел геометрии, изучающий фигуры,
- 4. Древнегреческий ученый
- 5. Слайд 5
- 6. Слайд 6
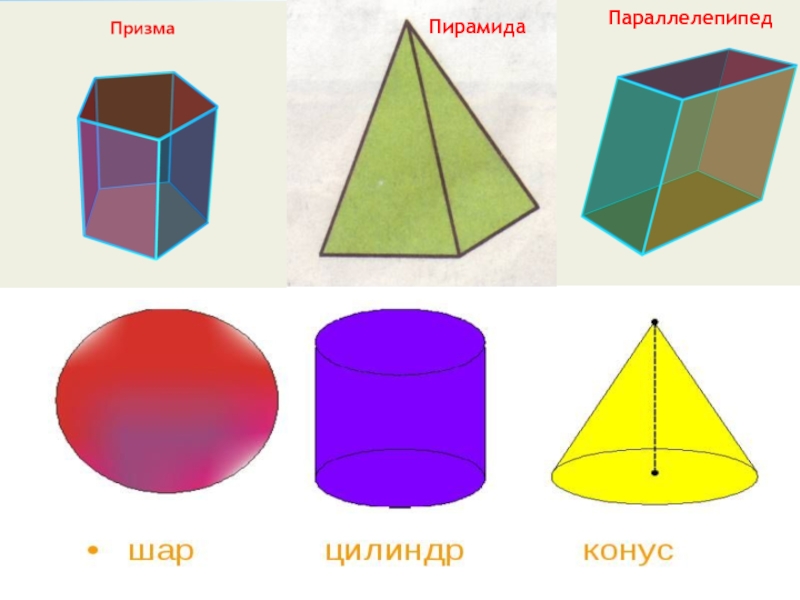
- 7. ПирамидаПирамидаПараллелепипед
- 8. Слайд 8
- 9. Слайд 9
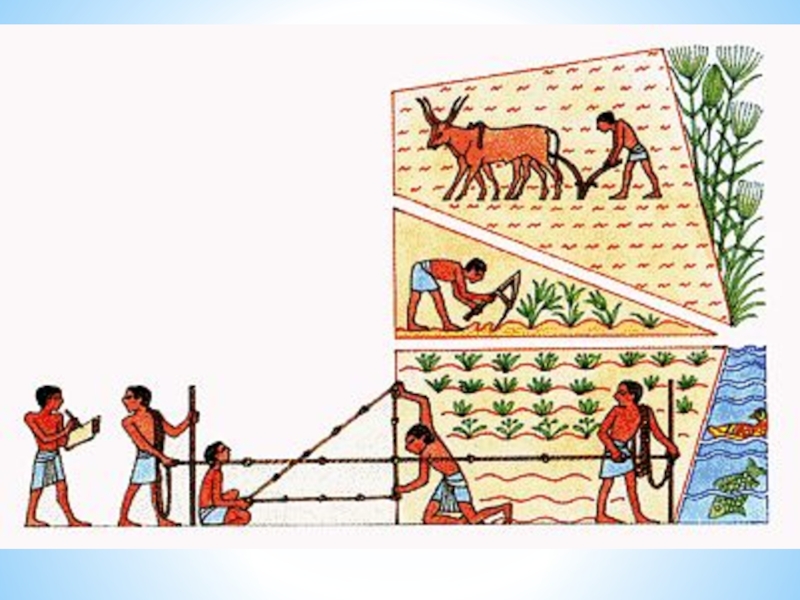
- 10. Стереометрия в машиностроении
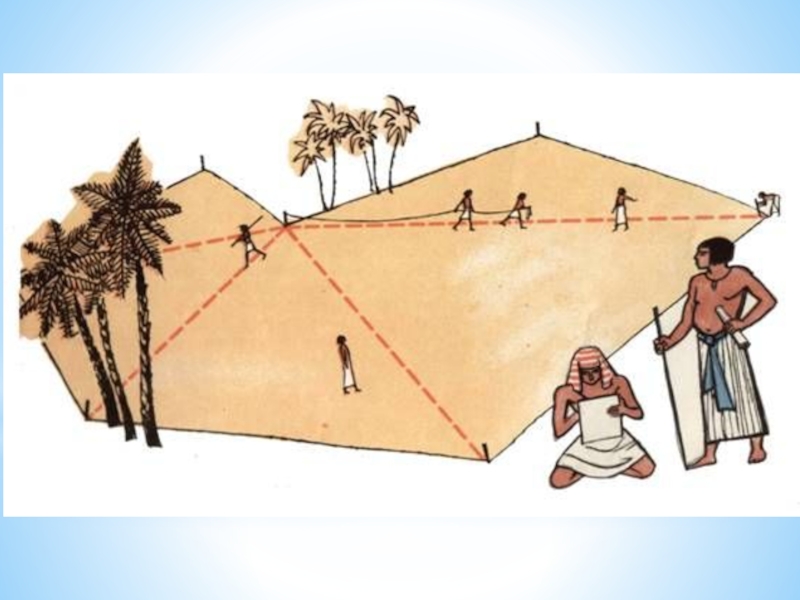
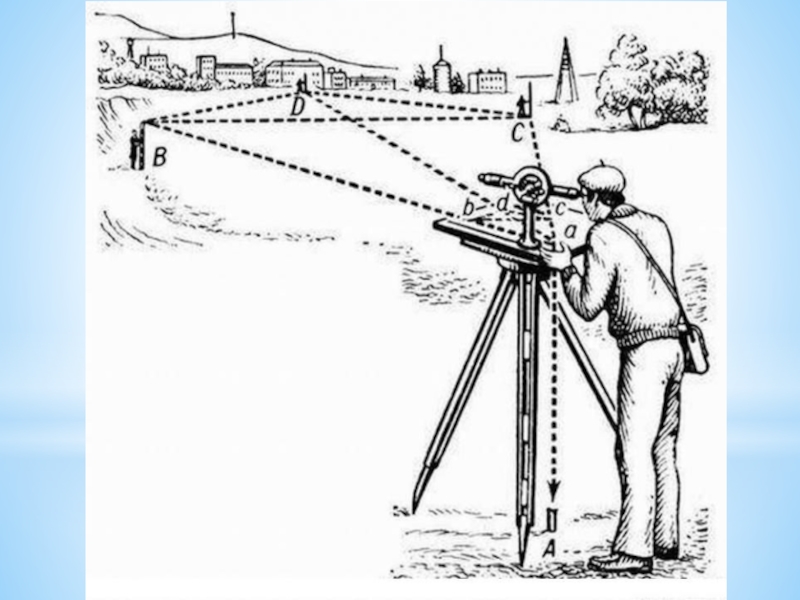
- 11. Стереометрия в геодезии
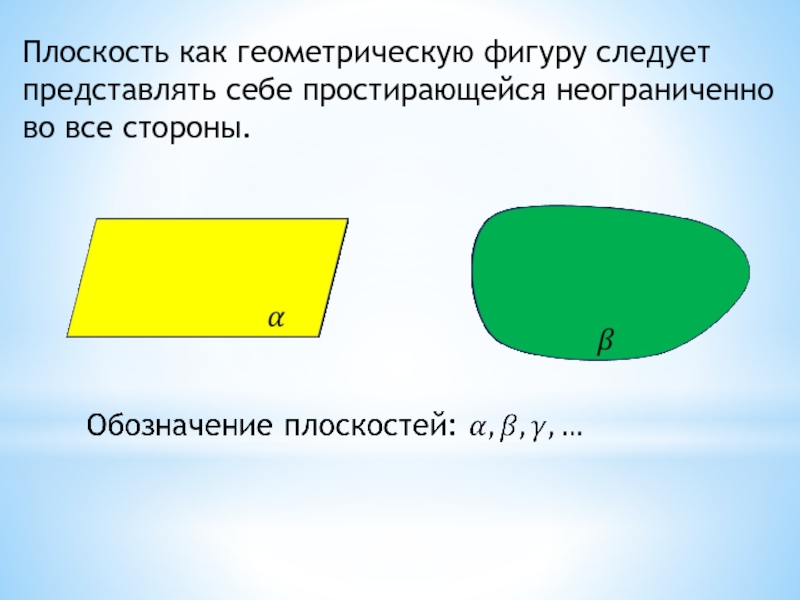
- 12. Плоскость как геометрическую фигуру следуетпредставлять себе простирающейся неограниченно во все стороны.
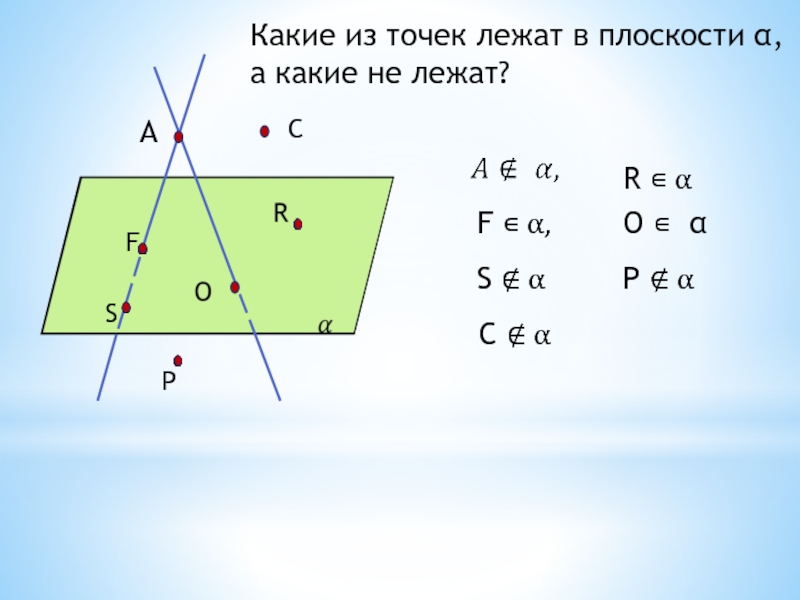
- 13. АСFSPКакие из точек лежат в плоскости α,а
- 14. Аксиома в переводе с толкового словаря С.И.
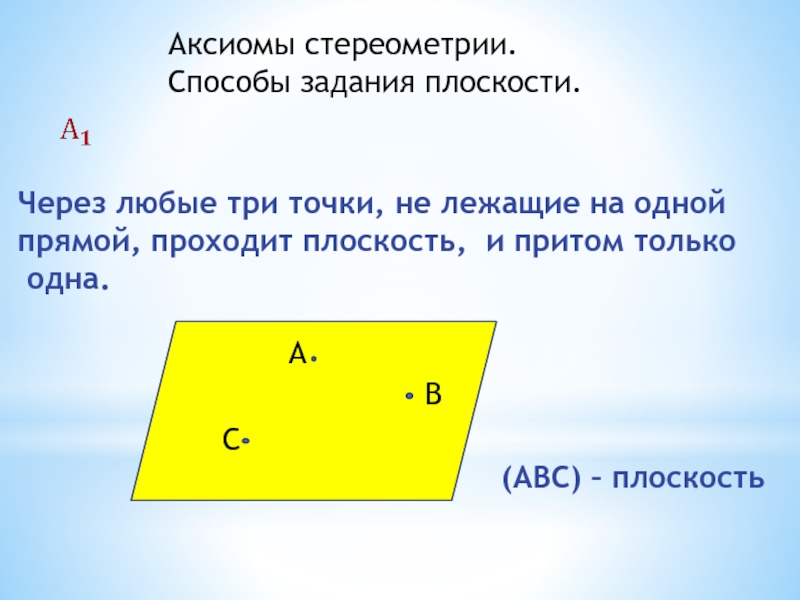
- 15. Аксиомы стереометрии. Способы задания плоскости. Через любые
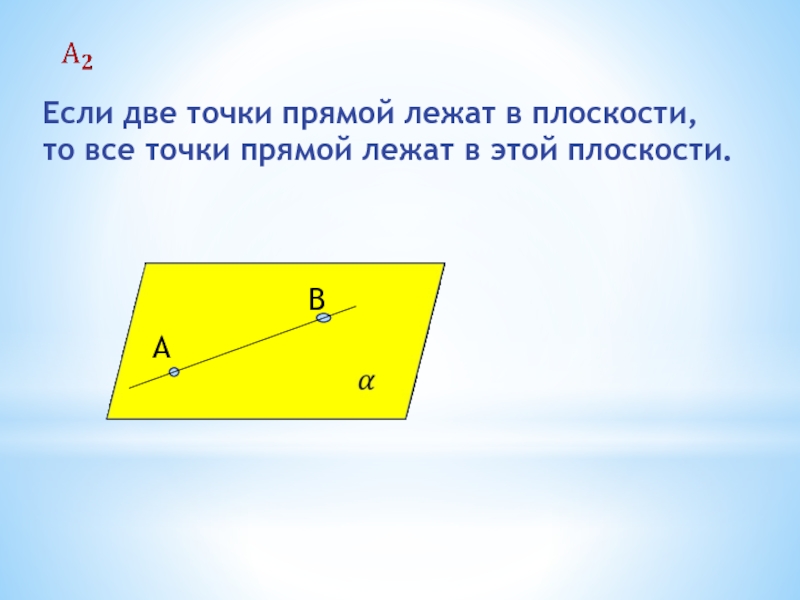
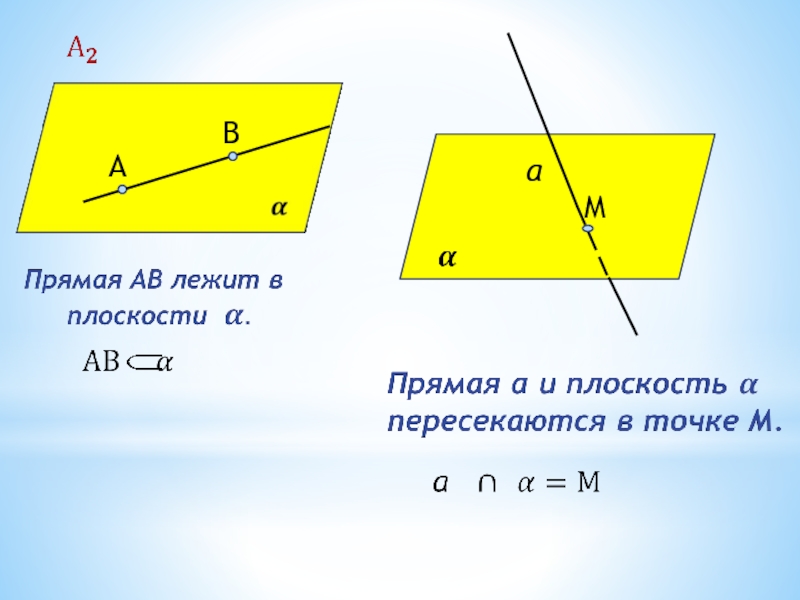
- 16. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.АВ
- 17. a
- 18. Если две плоскости имеют общую точку, то
- 19. №1 (а)Аналогично: МК лежит в (BCD).Точки В
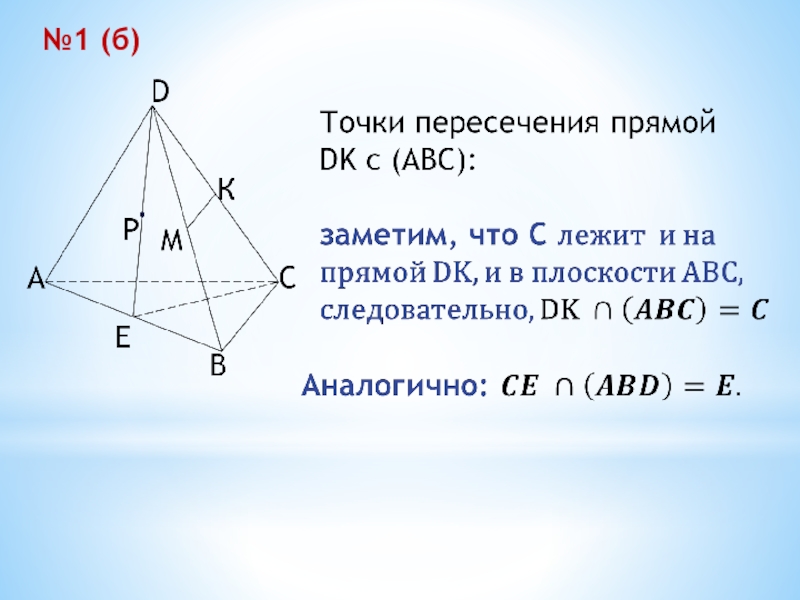
- 20. №1 (б)
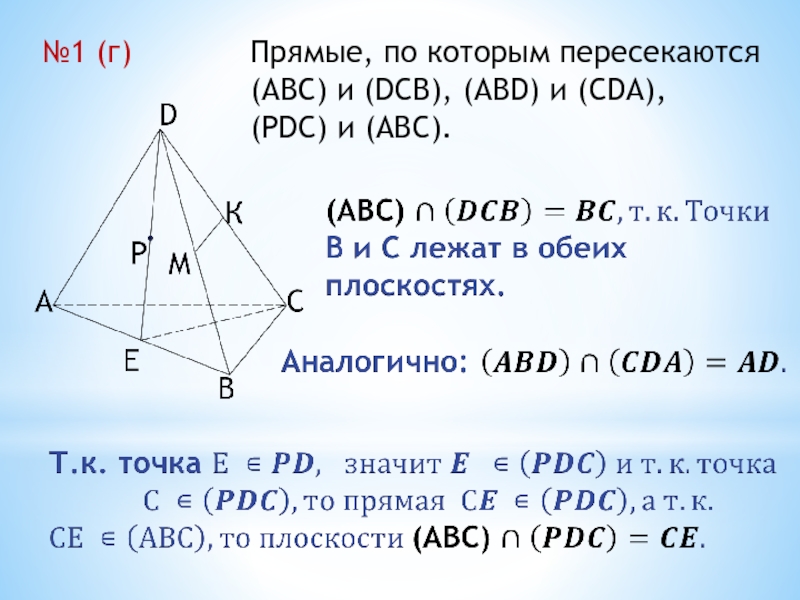
- 21. №1 (г)Прямые, по которым пересекаются(АВС) и (DCB), (ABD) и (CDA), (PDC) и (ABC).
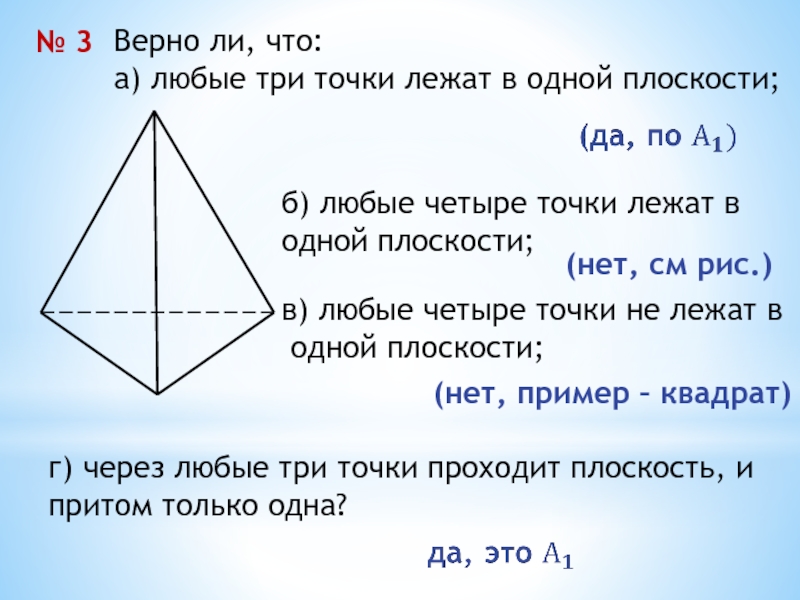
- 22. № 3Верно ли, что:а) любые три точки
- 23. Слайд 23
- 24. №5 Докажите, что через три данные точки
- 25. № 8.Верно ли утверждение:а) если две точки
- 26. № 10.Верно ли, что прямая лежит в
- 27. Определите, о каких аксиомах или следствиях из
- 28. На прямой две точки как-тоЗагордились, как могли:А
- 29. Если две прямыеВдруг пересекаются,Убежать от плоскостиПусть и
Слайд 3Стереометрия – это раздел геометрии, изучающий
фигуры, лежащие в пространстве.
От греческого
(«стереос» – объемный, пространственный ,
«метрео» – измерять.
Слайд 12Плоскость как геометрическую фигуру следует
представлять себе простирающейся неограниченно
во все стороны.
Слайд 14Аксиома в переводе с толкового словаря С.И. Ожегова означает исходное положение,
доказательств истинности других положений.
Портрет Ожегова С.И.
Слайд 15Аксиомы стереометрии.
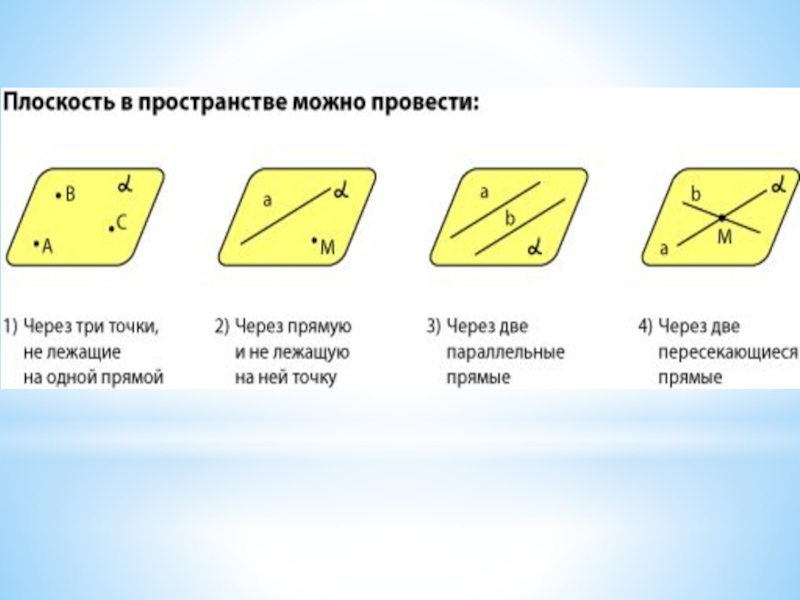
Способы задания плоскости.
Через любые три точки, не лежащие
прямой, проходит плоскость, и притом только
одна.
(АВС) – плоскость
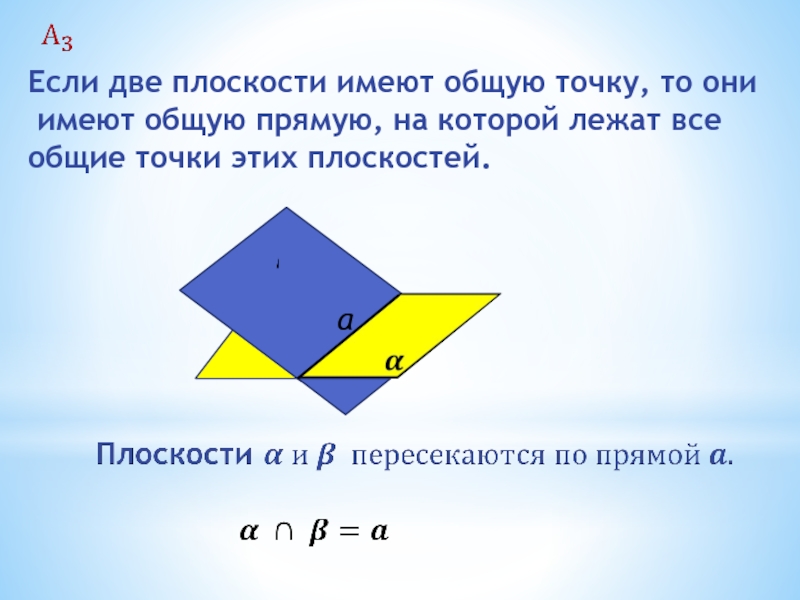
Слайд 18Если две плоскости имеют общую точку, то они
имеют общую прямую,
общие точки этих плоскостей.
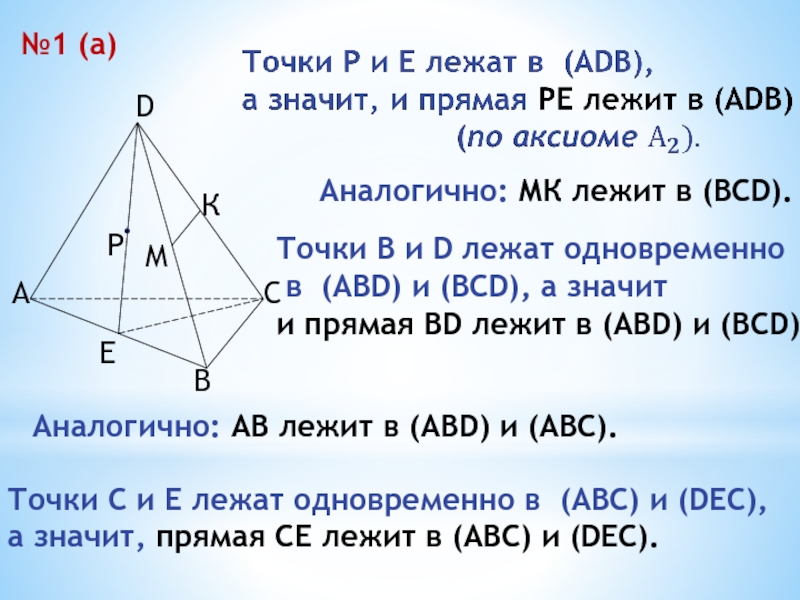
Слайд 19№1 (а)
Аналогично: МК лежит в (BCD).
Точки В и D лежат одновременно
и прямая BD лежит в (ABD) и (BCD)
Аналогично: АВ лежит в (АBD) и (АВС).
Точки С и Е лежат одновременно в (АВС) и (DEC),
а значит, прямая СЕ лежит в (АВС) и (DEC).
Слайд 22№ 3
Верно ли, что:
а) любые три точки лежат в одной плоскости;
б) любые четыре точки лежат в
одной плоскости;
(нет, см рис.)
в) любые четыре точки не лежат в
одной плоскости;
(нет, пример – квадрат)
г) через любые три точки проходит плоскость, и
притом только одна?
Слайд 24№5
Докажите, что через три данные точки ,
лежащие на одной
Сколько существует таких плоскостей?
Возьмем четвертую точку, не лежащую на
этой прямой. Через прямую и не лежащую
на ней точку можно провести плоскость
(следствие из аксиомы).
Таких плоскостей бесконечно много, т.к.
четвертую точку можно выбирать произвольно.
Слайд 25№ 8.
Верно ли утверждение:
а) если две точки окружности лежат в плоскости,
нет, окружность можно вращать вокруг прямой,
соединяющей эти две точки
б) если три точки окружности лежат в плоскости,
то и вся окружность лежит в этой плоскости.
Да.
Слайд 26№ 10.
Верно ли, что прямая лежит в плоскости данного
треугольника, если
а) пересекает две стороны треугольника;
да
б) проходит через одну из вершин треугольника.
Слайд 27Определите, о каких аксиомах или следствиях
из них идет речь.
На трех
На синих трех морях.
На трех китах стоит Земля,
На трех больших китах.
Три точки – это якоря
Для плоскости одной.
И хоть в китов не верю я,
Но пусть по плоскости меня
Сейчас троллейбус номер «три»
Быстрей домой умчит.
Слайд 28На прямой две точки как-то
Загордились, как могли:
А у нас особый статус,
Ведь
Теорема им в два счета,
Гордым точкам, доказала:
В плоскости – не только точки,
В ней лежит и вся прямая!
Слайд 29Если две прямые
Вдруг пересекаются,
Убежать от плоскости
Пусть и не стараются!
Через эти две
Плоскость точно уж пройдет.
А другую – не старайся, все равно не проведешь!