- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Аксиомы стереометрии
Содержание
- 1. Презентация по геометрии на тему Аксиомы стереометрии
- 2. Изучает свойства геометрических фигур на плоскостиИзучает свойства
- 3. ПланиметрияСтереометрияНаряду с этими фигурами мы будем рассматривать
- 4. Для обозначение точек используем прописные латинские буквыДля
- 5. Плоскости будем обозначать греческими буквами. На рисунках
- 6. Многогранники:Куб.Параллелепипед.Пирамида.
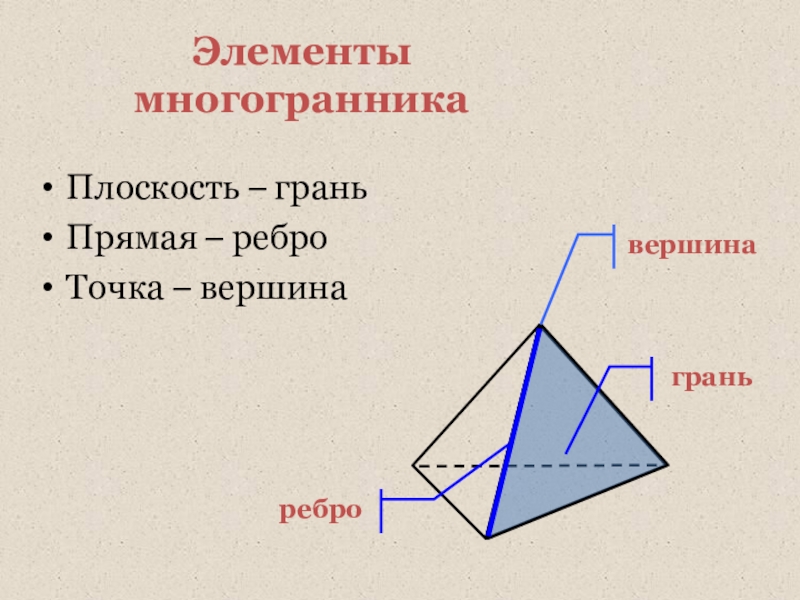
- 7. Элементы многогранникаПлоскость – граньПрямая – реброТочка – вершинавершинаграньребро
- 8. Аксиома(от греч. axíõma – принятие положения)исходное положение научной теории, принимаемое без доказательства
- 9. Аксиомы стереометрии описывают:А1.А2. А3. АВССпособ задания плоскостиАВВзаимное расположение прямой и плоскостиВзаимное расположение плоскостей
- 10. А1. Через любые три точки, не
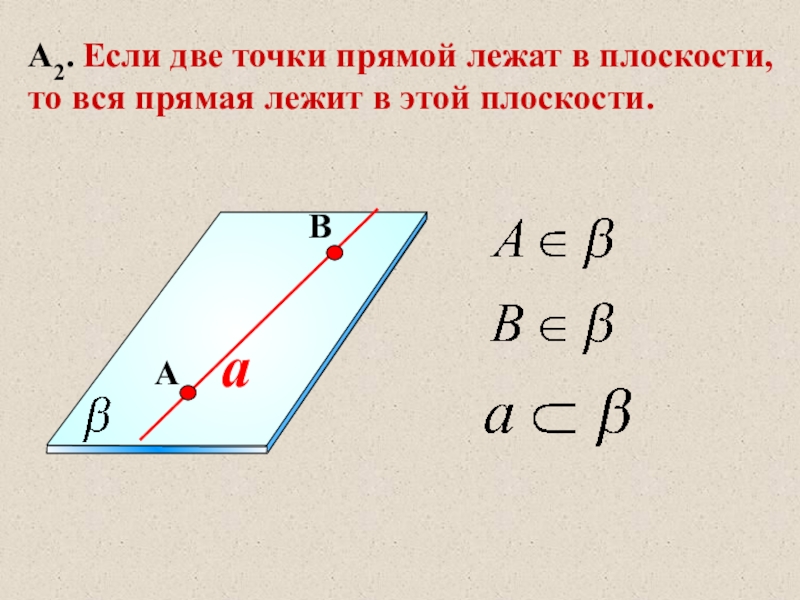
- 11. aА2. Если две точки прямой лежат в плоскости, то вся прямая лежит в этой плоскости. AB
- 12. aА3. Если две плоскости имеют общую точку, то они пересекаются по прямой, содержащей эту точку.
- 13. А1. Через любые три точки, не
- 14. Прочти чертежAС
- 15. Прочти чертежBcba
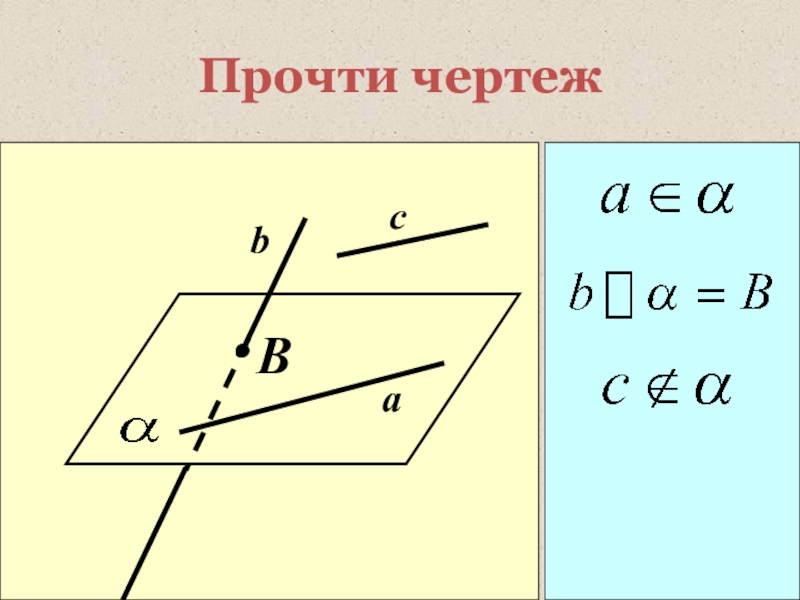
- 16. Прочти чертеж
- 17. Взаимное расположение прямой и плоскости.Прямая лежит в
- 18. СЛЕДСТВИЯ ИЗ АКСИОМ
- 19. Способы задания плоскости1. Три точка, не лежащие
- 20. Способы задания плоскости3. Две пересекающиеся прямыеТеорема 2Теорема 34. Две параллельные прямыеg
- 21. Пользуясь данным рисунком, назовите:а) четыре
- 22. Пользуясь данным рисунком, назовите:а) две
- 23. Пользуясь данным рисунком, назовите:а) три
- 24. №1.Дана треугольная призмаАВСА1В1С1. М принадлежит АВ.Построить
- 25. D1ВАDС1СВ1РА1№2.Дан куб АВСDА1В1С1D1Р принадлежит ВВ1.ВР = В1Р.Как
- 26. D1ВАDС1СВ1РА1№3.Дан куб АВСDА1В1С1D1Р принадлежит ВВ1.ВР = В1РКак
Слайд 2Изучает свойства геометрических фигур на плоскости
Изучает свойства фигур в пространстве
В переводе
«гео» – по-гречески земля, «метрео» – мерить
Слово «стереометрия» происходит от греческих слов «стереос» объемный, пространственный, «метрео» – мерить
Слайд 3Планиметрия
Стереометрия
Наряду с этими фигурами мы будем рассматривать геометрические тела и их
Куб, параллелепипед, призма, пирамида.
Шар, сфера, цилиндр, конус.
Основные фигуры: точка, прямая
Основные фигуры: точка, прямая, плоскость
Другие фигуры: отрезок, луч, треугольник, квадрат, ромб, параллелограмм, трапеция, прямоугольник, выпуклые и невыпуклые n-угольники, круг, окружность, дуга и др.
Изучение нового материала.
Слайд 4Для обозначение точек используем прописные латинские буквы
Для обозначение прямых используем строчные
Или обозначаем прямую двумя прописными латинскими буквами.
Слайд 5Плоскости будем обозначать греческими буквами.
На рисунках плоскости обозначаются в виде
Слайд 8Аксиома
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без
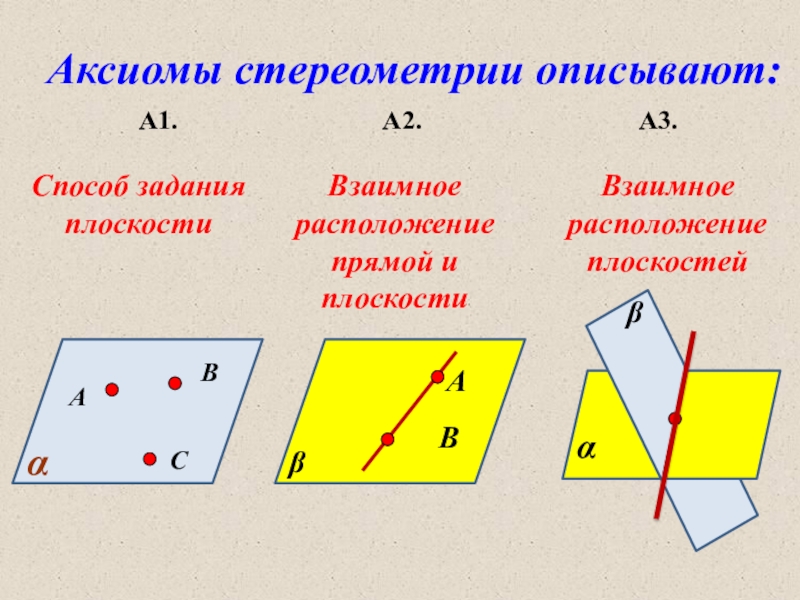
Слайд 9Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
Способ задания плоскости
А
В
Взаимное расположение прямой и плоскости
Взаимное
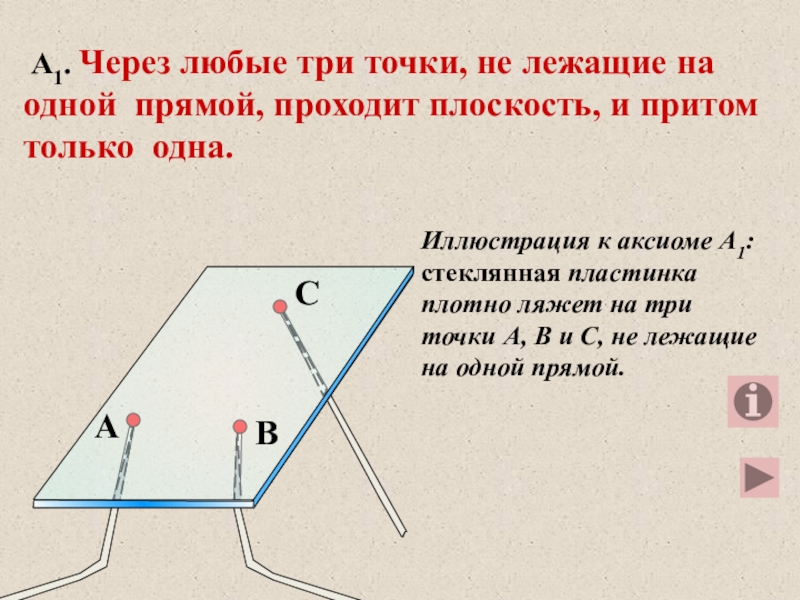
Слайд 10 А1. Через любые три точки, не лежащие на одной прямой,
Иллюстрация к аксиоме А1: стеклянная пластинка плотно ляжет на три точки А, В и С, не лежащие на одной прямой.
A
B
C
Слайд 12a
А3. Если две плоскости имеют общую точку, то они пересекаются по
Слайд 13 А1.
Через любые три точки, не лежащие на одной прямой,
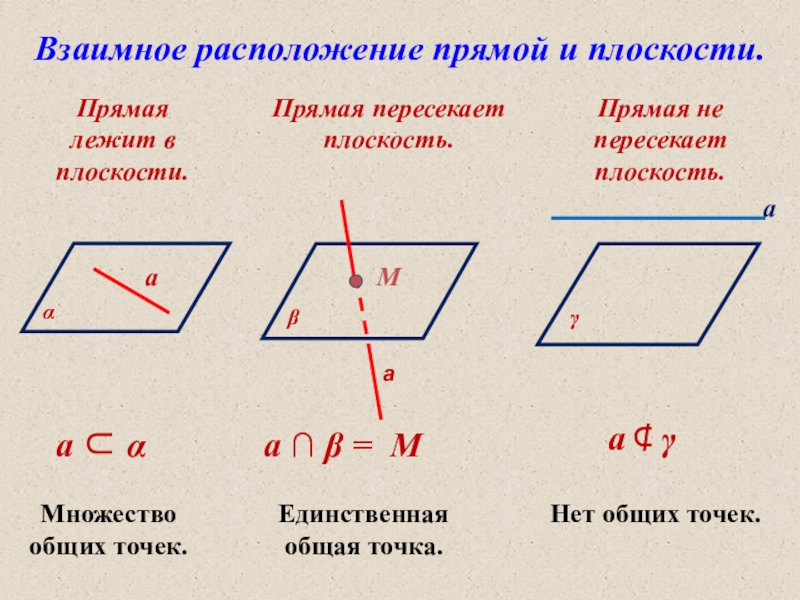
Слайд 17Взаимное расположение прямой и плоскости.
Прямая лежит в плоскости.
Прямая пересекает плоскость.
Прямая не
Множество общих точек.
Единственная общая точка.
Нет общих точек.
а
а
М
g
а
а
а ∩ = М
а ⊄
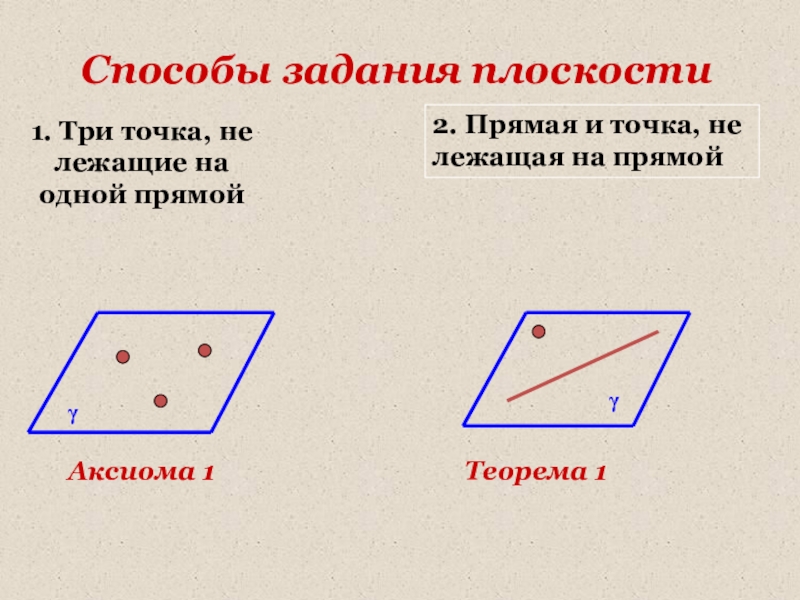
Слайд 19Способы задания плоскости
1. Три точка, не лежащие на одной прямой
2. Прямая
Аксиома 1
Теорема 1
Слайд 20Способы задания плоскости
3. Две пересекающиеся прямые
Теорема 2
Теорема 3
4. Две параллельные прямые
g
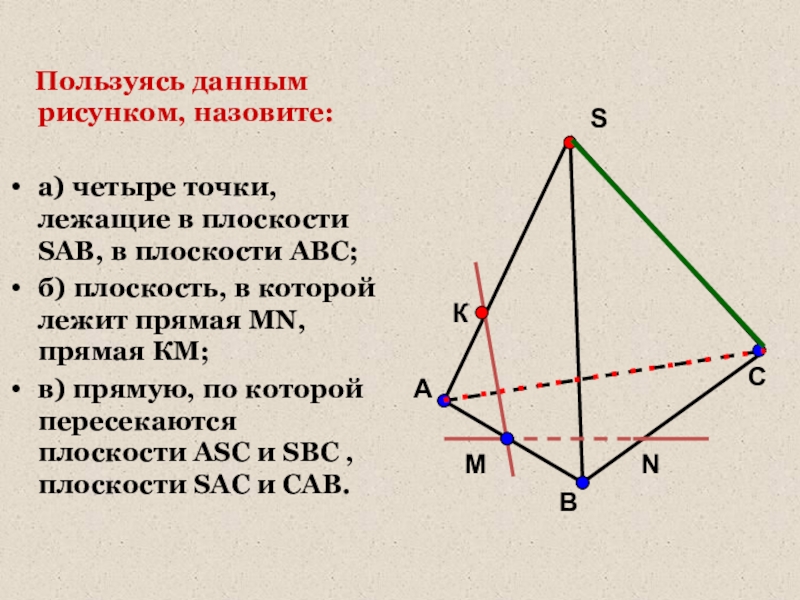
Слайд 21 Пользуясь данным рисунком, назовите:
а) четыре точки, лежащие в плоскости
б) плоскость, в которой лежит прямая MN, прямая КМ;
в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.
Слайд 22 Пользуясь данным рисунком, назовите:
а) две плоскости, содержащие прямую DE
б) прямую, по которой пересекаются плоскости
DEF и SBC; плоскости FDE и SAC ;
в) две плоскости, которые пересекает прямая SB; прямая AC .
Слайд 23 Пользуясь данным рисунком, назовите:
а) три плоскости, содержащие прямую В1С;
б) прямую, по которой пересекаются плоскости
B1CD и AA1D1 ; плоскости ADC1 и A1B1B ;
в) плоскость, не пересекающуюся с прямой CD1 ; с прямой BC1
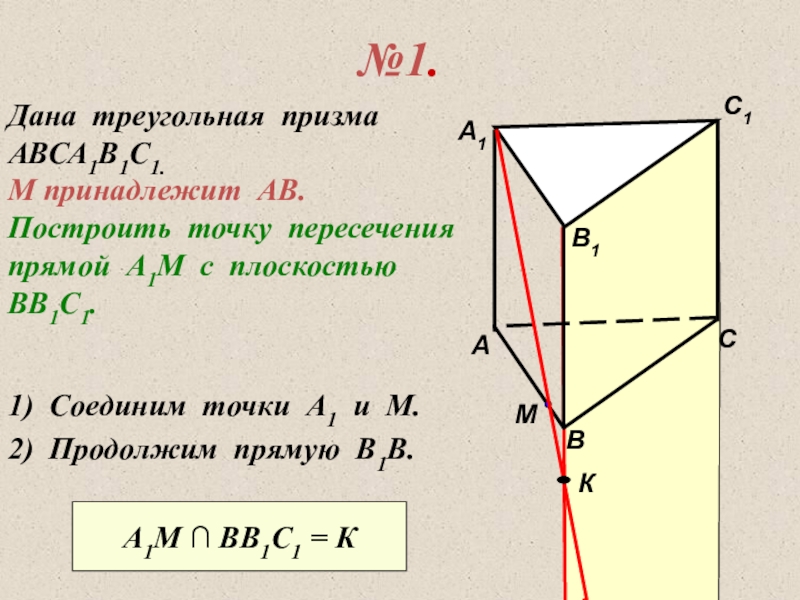
Слайд 24№1.
Дана треугольная призма
АВСА1В1С1.
М принадлежит АВ.
Построить точку пересечения
прямой А1М с
ВВ1С1.
А
В
С1
С
В1
А1
М
1) Соединим точки А1 и М.
2) Продолжим прямую В1В.
К
А1М ∩ ВВ1С1 = К
Слайд 25D1
В
А
D
С1
С
В1
Р
А1
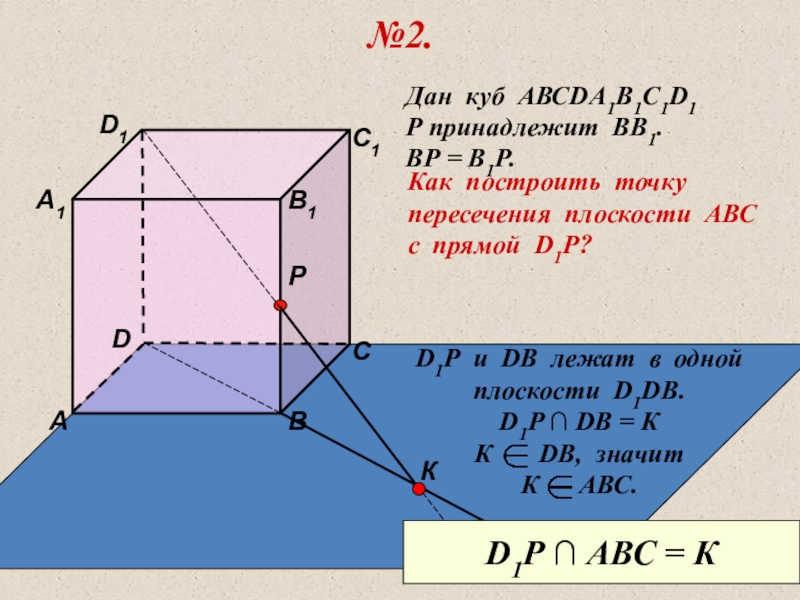
№2.
Дан куб АВСDА1В1С1D1
Р принадлежит ВВ1.
ВР = В1Р.
Как построить точку
пересечения плоскости
с прямой D1P?
К
D1Р u DB лежат в одной
плоскости D1DB.
D1P ∩ DB = К
К DB, значит
К АВС.
D1P ∩ АВС = К
Слайд 26D1
В
А
D
С1
С
В1
Р
А1
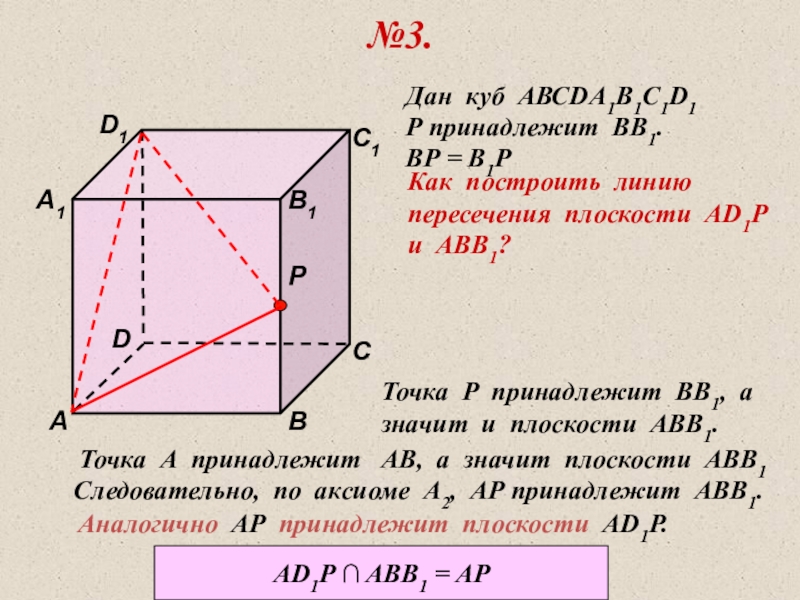
№3.
Дан куб АВСDА1В1С1D1
Р принадлежит ВВ1.
ВР = В1Р
Как построить линию
пересечения плоскости
и АВВ1?
Точка Р принадлежит ВВ1, а
значит и плоскости АВВ1.
Точка А принадлежит АВ, а значит плоскости АВВ1
Следовательно, по аксиоме А2, АР принадлежит АВВ1.
Аналогично АР принадлежит плоскости АD1P.
АD1P ∩ ABB1 = AP