- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии для 8 класса Теорема Пифагора
Содержание
- 1. Презентация по геометрии для 8 класса Теорема Пифагора
- 2. Проблемные вопрос«Всегда ли равны пифагоровы штаны?»
- 3. Цели:Рассмотреть историю теоремы;Историческое значение имени Пифагора;Различные доказательства.
- 4. ГипотезаЗнания о различных способах доказательства теоремы дают возможность научиться решать задачи различными способами.
- 5. История теоремы
- 6. История теоремы Веревочным треугольником со сторонами 3,4
- 7. История теоремы Египтяне придумали задачу о лотосе. "На
- 8. История теоремы Заслуга же Пифагора
- 9. Доказательство ан-Найризия Доказательство ан-Найризия тоже
- 10. Доказательство ан-Найризия
- 11. Доказательство Мёльманна Дано: ΔАВС - прямоугольный.Доказательство: Площадь
- 12. Доказательство ВальдхеймаЭто доказательство также имеет вычислительный характер.
- 13. Доказательство индийского математика Бхаскари Рассмотрим квадрат, показанный
- 14. Доказательство Перигаля Доказательство Перигаля очень легкое. Два
- 15. Применение на практике Диагональ квадрата. Диагональ d квадрата
- 16. Применение на практике Теорема Пифагора используется
- 17. Применение на практике Если, например,
Проблемные вопрос«Всегда ли равны пифагоровы штаны?»
Слайд 3Цели:
Рассмотреть историю теоремы;
Историческое значение имени Пифагора;
Различные доказательства.
Слайд 4Гипотеза
Знания о различных способах доказательства теоремы дают
возможность научиться решать задачи
различными способами.
Слайд 5История теоремы
Теорема Пифагора –
важнейшее утверждение геометрии. Даже те, кто в своей жизни навсегда «распрощался» с математикой, сохраняют воспоминания о «пифагоровых штанах».
Причина такой популярности теоремы Пифагора объясняется ее простотой, красотой, значимостью. Изучение вавилонских, древнекитайских рукописей показало, что это утверждение было известно задолго до Пифагора.
Причина такой популярности теоремы Пифагора объясняется ее простотой, красотой, значимостью. Изучение вавилонских, древнекитайских рукописей показало, что это утверждение было известно задолго до Пифагора.
Слайд 6История теоремы
Веревочным треугольником со сторонами 3,4 и 5 единиц пользовались
еще в Древнем Египте для построения прямых углов на местности
Слайд 7История теоремы
Египтяне придумали задачу о лотосе.
"На глубине 12 футов растет
лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну."
Слайд 8История теоремы
Заслуга же Пифагора состояла в том, что
он доказал эту теорему. Древняя легенда свидетельствует о том, что он в честь этого открытия принес в жертву быка или даже 100 быков.
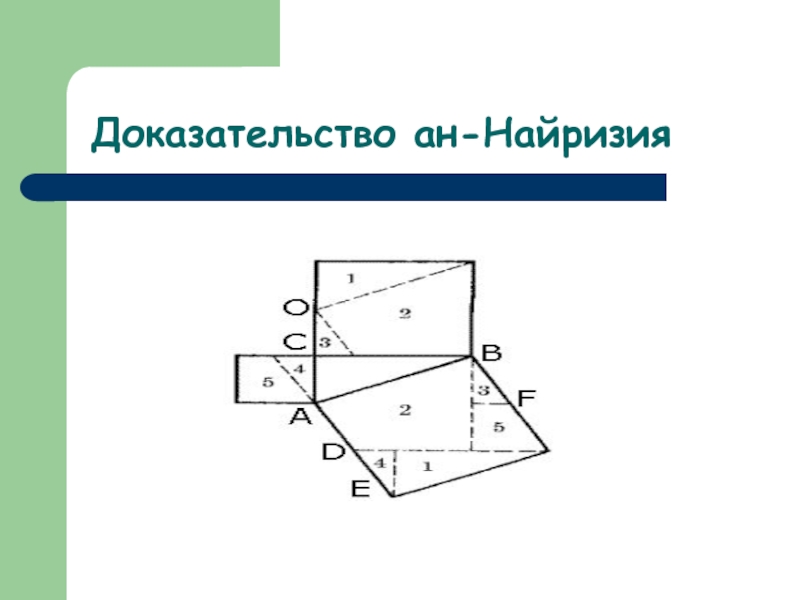
Слайд 9Доказательство ан-Найризия
Доказательство ан-Найризия тоже довольно легкое. Оно примечательно
тем, что все фигуры совпадают с равными им исключительно при параллельном переносе.
Дано: при разделении на фигуры надо учитывать, что DE=BF.
Доказательство:
По чертежу ясно видно, что фигуры, отмеченные одинаковыми цифрами, равны. Треугольники 1 и 1, 3 и 3, 4 и 4 равны между собой. Четырехугольники 2 и 2, 5 и 5 также равны. Следовательно, теорема доказана.
Слайд 11Доказательство Мёльманна
Дано: ΔАВС - прямоугольный.
Доказательство: Площадь данного прямоугольного треугольника, с
одной стороны равна ab/2, а с другой - pr/2, где p - полупериметр треугольника, а r - радиус вписанной окружности. Вспомним, что r = (a + b - c)/2. Имеем:
ab/2 = pr/2 = (a + b + c)/2 * (a + b - c)/2.
откуда следует, что a2 + b2 = c2. Теорема доказана.
откуда следует, что a2 + b2 = c2. Теорема доказана.
Слайд 12Доказательство Вальдхейма
Это доказательство также имеет вычислительный характер. Можно использовать рисунки для
доказательства основанного на вычислении площадей двумя способами.
Для того, чтобы доказать теорему пользуясь первым рисунком достаточно только выразить площадь трапеции двумя путями.
S трапеции =(a+b)²/2
S трапеции =a²b²+c²/2
Приравнивая правые части получим:
a²+b²=c²
Теорема доказана.
Для того, чтобы доказать теорему пользуясь первым рисунком достаточно только выразить площадь трапеции двумя путями.
S трапеции =(a+b)²/2
S трапеции =a²b²+c²/2
Приравнивая правые части получим:
a²+b²=c²
Теорема доказана.
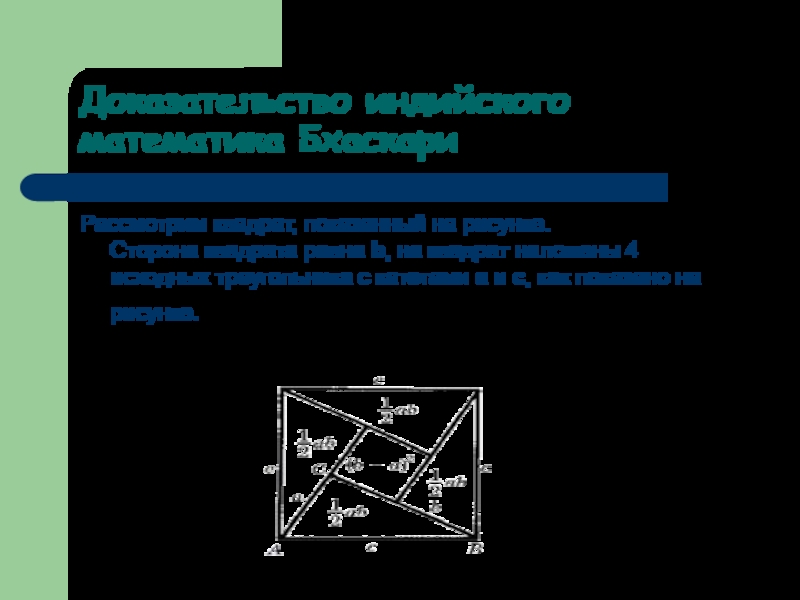
Слайд 13Доказательство индийского математика Бхаскари
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна
b, на квадрат наложены 4 исходных треугольника с катетами a и c, как показано на рисунке.
Слайд 14Доказательство Перигаля
Доказательство Перигаля очень легкое. Два квадрата, построенные на катетах,
расположены рядом. Надо разделить эту фигуру всего на 3(!) части, чтобы сложить из них квадрат на гипотенузе. На иллюстрации наглядно дано это разрезание.
Слайд 15Применение на практике
Диагональ квадрата. Диагональ d квадрата со стороной а можно
рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом,
d²=2a².
d²=2a².
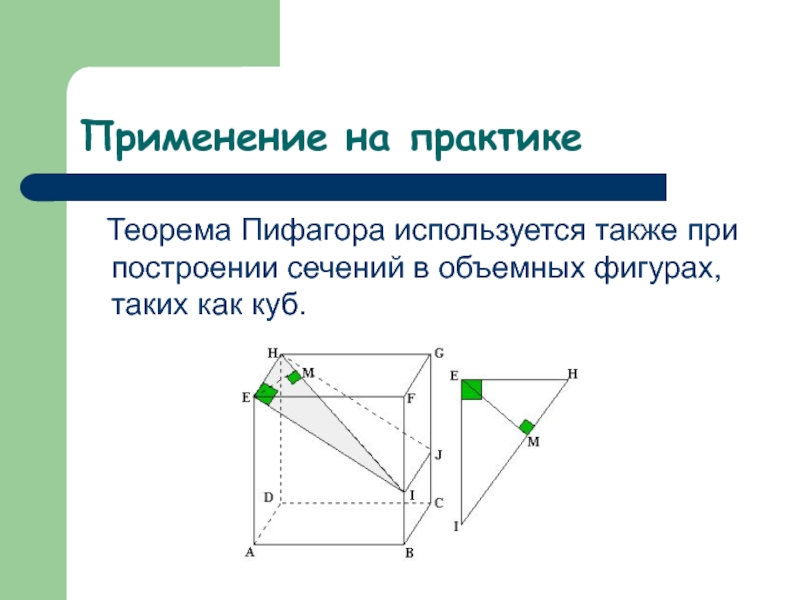
Слайд 16Применение на практике
Теорема Пифагора используется также при построении сечений
в объемных фигурах, таких как куб.
Слайд 17Применение на практике
Если, например, рассматривать нашу четырехугольную пирамиду
как крышу башни, то в первом нашем вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчете стоимости кровельных работ. Заметим, что расчет площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит:
"Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь."
"Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь."