- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии для 10 класса по теме Перпендикуляр и наклонная
Содержание
- 1. Презентация по геометрии для 10 класса по теме Перпендикуляр и наклонная
- 2. Презентация по геометрии учителя математики МКОУ СОШ
- 3. Урок №1 Расстояние от точки до плоскости
- 4. Расстояние от точки до плоскостиαАНМОтрезок АН –
- 5. Свойство наклонных и их проекций: Если из
- 6. №143 1. МО (АВС).
- 7. Расстояние между параллельными плоскостямиАМА0М0ХХ0αβАА0
- 8. № 144: Если прямая (а) параллельна плоскости
- 9. Расстояние между прямой и параллельной ей плоскостьюаαАВВсе
- 10. Решение задач: №138а,139,140,143 Домашнее задание:
- 11. Урок 2
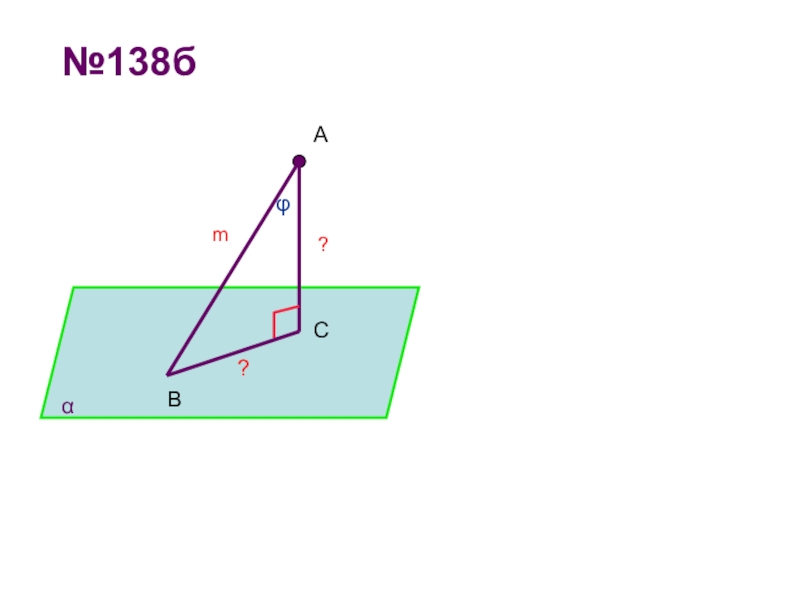
- 12. №138бСАВαφ??m
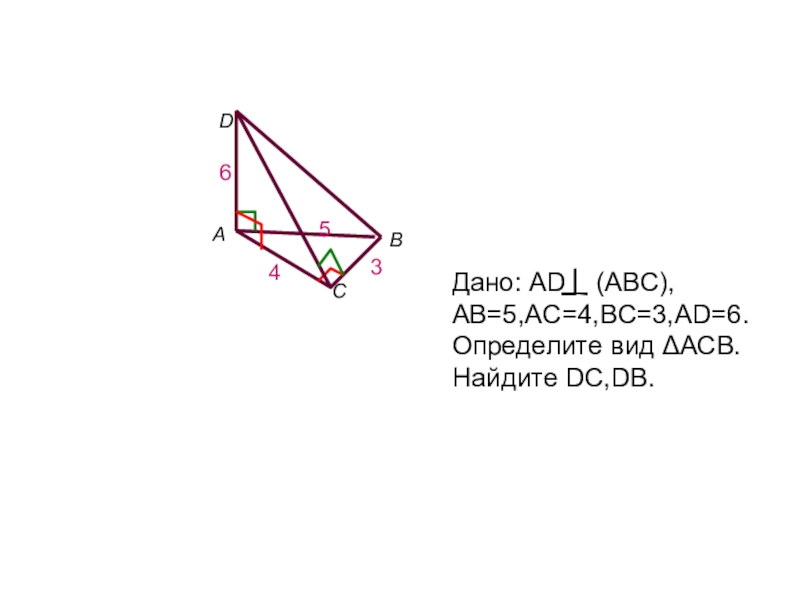
- 13. АВСDДано: AD (ABC), AB=5,AC=4,ВC=3,AD=6.Определите вид ΔАСВ. Найдите DC,DB.5436
- 14. Теорема о трёх перпендикулярахαАНМаПрямая, проведённая в плоскости
- 15. 3. Установите по рисункам положение прямых а и b.АВСDbаFb1 АВFaCDbABFabCDABCD – ромб.ABFabCDABCD – ромб.
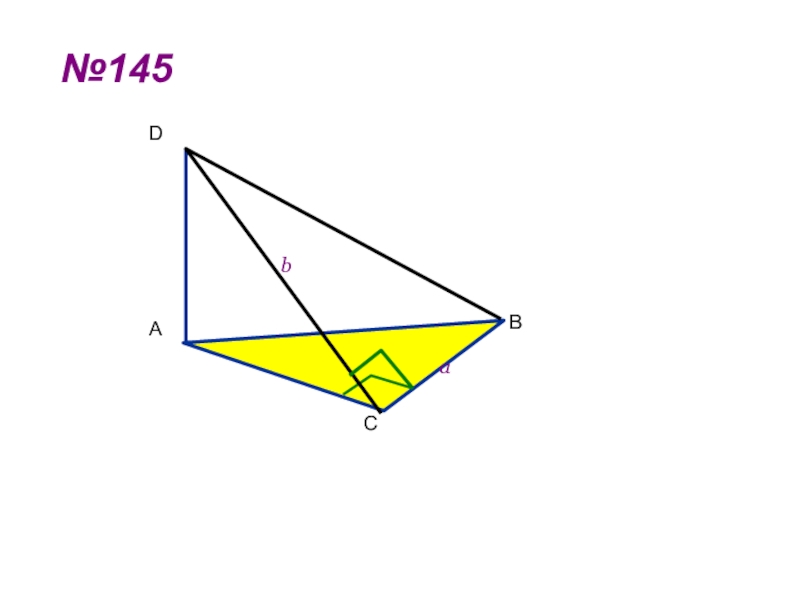
- 16. №145CADBab
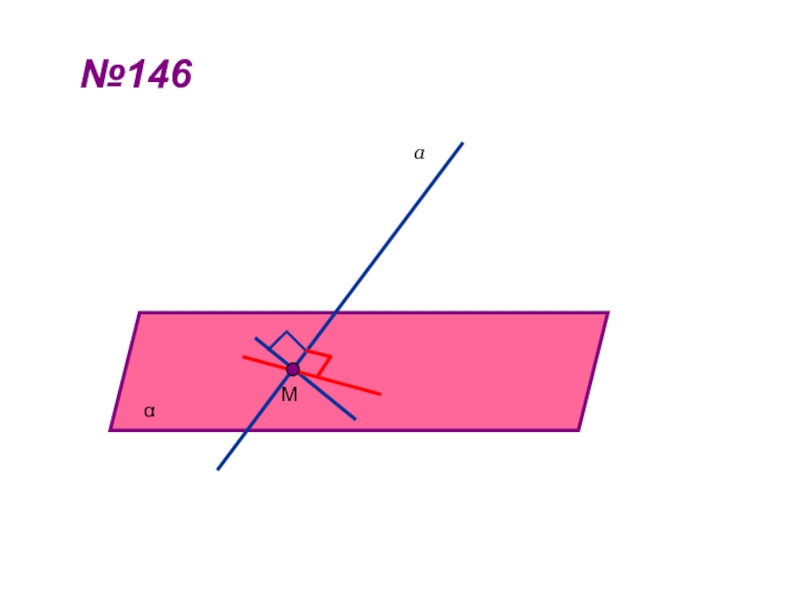
- 17. №146αаМ
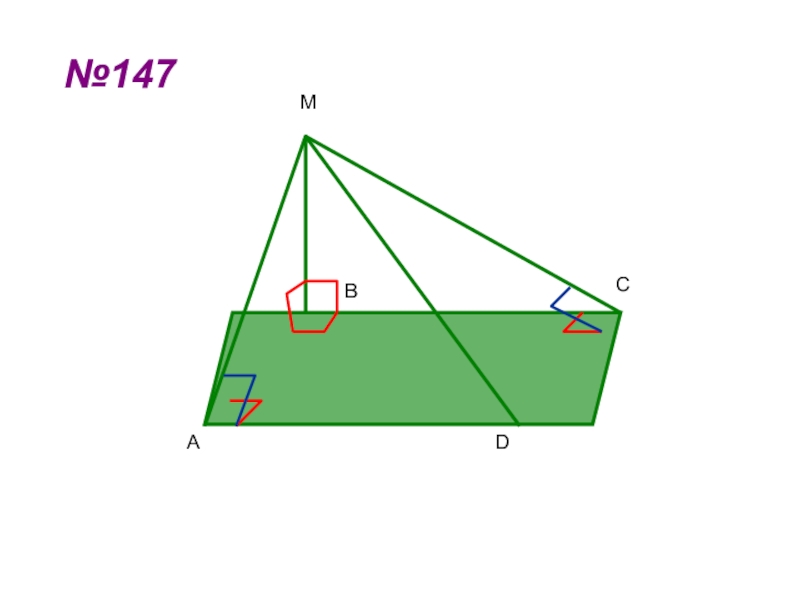
- 18. №147АВСDM
- 19. Домашнее задание: № 148,149,150
- 20. Урок 3Решение задач по теме «Теорема о трёх перпендикулярах»
- 21. АВСаа11.Верно ли утверждение: « Если прямая, принадлежащая
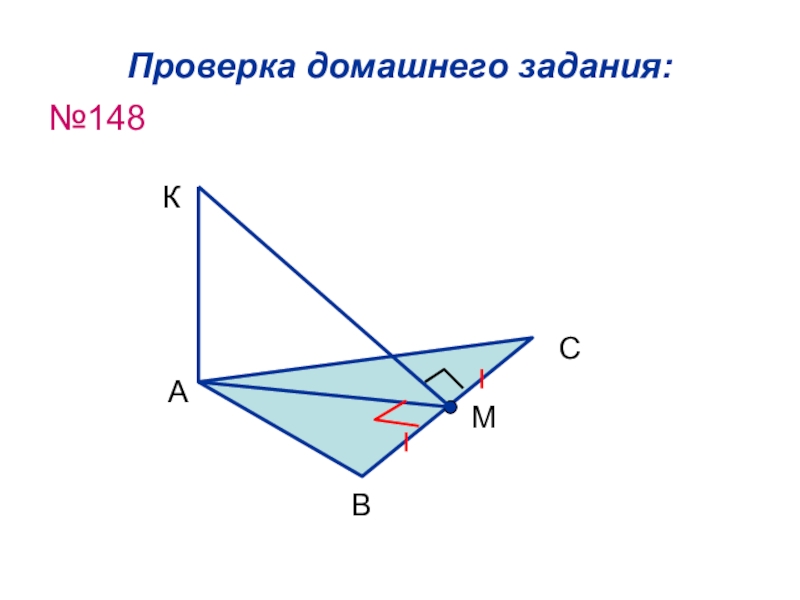
- 22. Проверка домашнего задания:№148АВСКМ
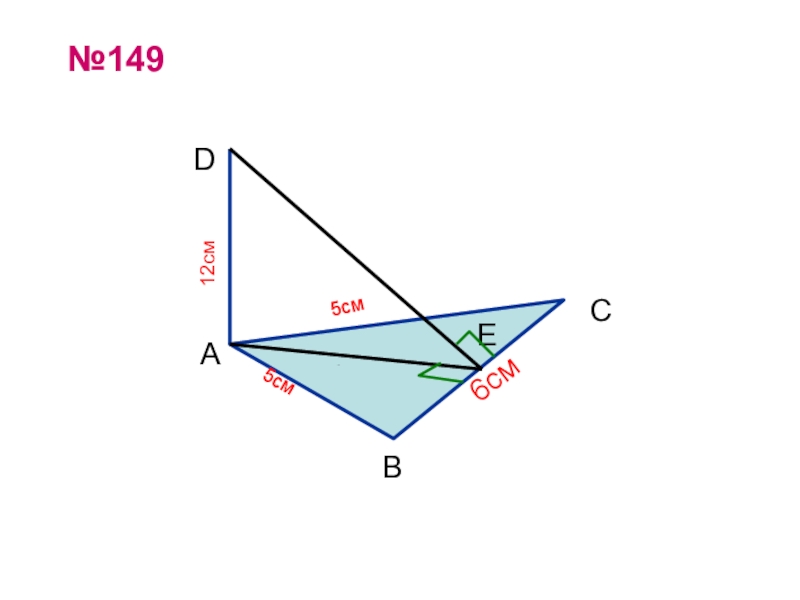
- 23. №149АВСDЕ5см5см12см6см4см4 10
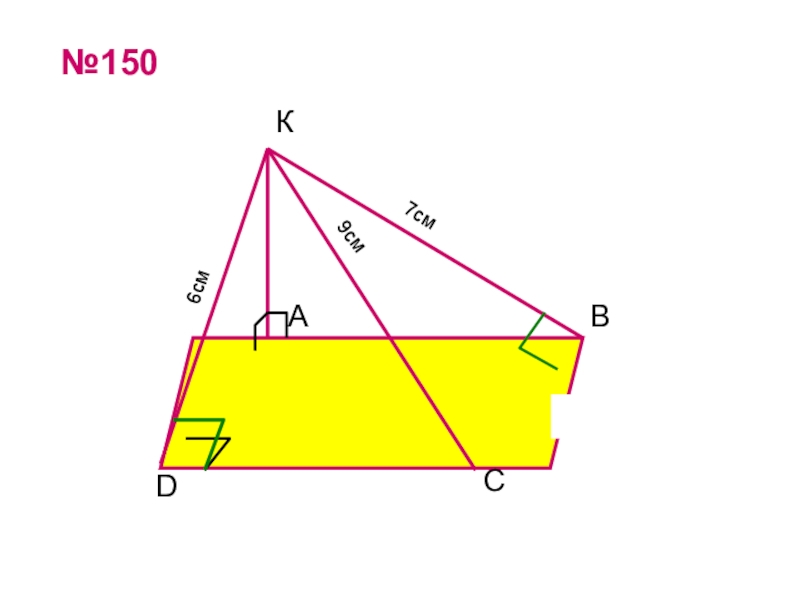
- 24. №150АВСDК6см7см9см45см2см4 2см
- 25. 1. AF (ABC). Найти расстояние от
- 26. Устные задачи на готовых чертежах:1.АА1ВВ1СС1DАВСD – куб.
- 27. 5.ABCDABCD – параллелограмм, ВМ
- 28. Решение задач: №154,156. Домашнее задание: №155, 159.
- 29. Урок 4Решение задач по теме «Теорема о трёх перпендикулярах»
- 30. Слайд 30
- 31. №159ВСDАМЕ1) МЕ ІІAD,DEІІΑМ; 2) AM
- 32. Важная задача: Если точка равноудалена от всех
- 33. Решение задач по готовым рисункам из урока 10Домашнее задание: № 160, 205
- 34. Урок 5Угол между прямой и плоскостью
- 35. Проверка домашнего задания №160αβАDCB1)ВD α, ACІІ BD.
- 36. №205СDАВ3дм1дмЕАЕ=ВЕ=СЕ=2√2см, МЕ2=(2√7)2+(2√2)2= =28+8=36, МЕ = 6(см)2дмАСВЕ
- 37. Прямоугольная проекция фигуры на плоскостьММ1FF1Проекцией точки на
- 38. Свойство 1: Проекция прямой на плоскость, не
- 39. № 162: Доказать, что угол(φ0 ) между
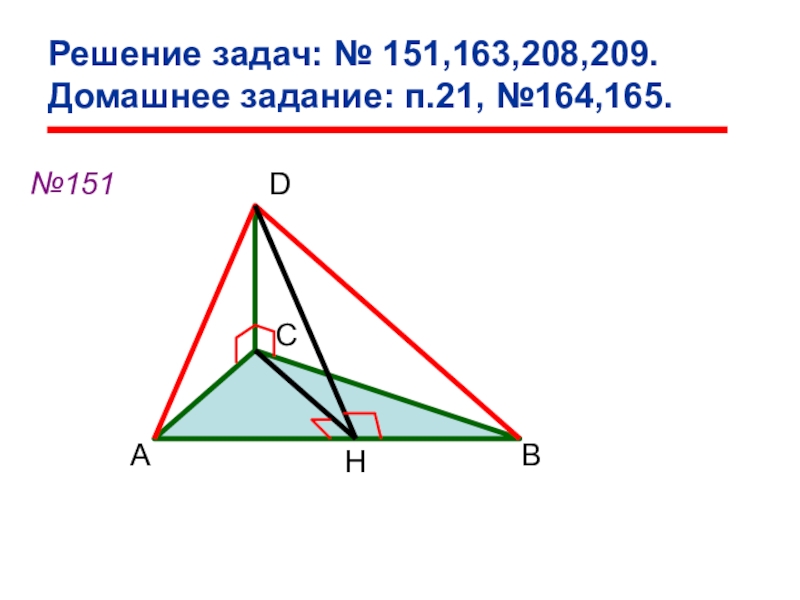
- 40. Решение задач: № 151,163,208,209. Домашнее задание: п.21, №164,165.№151АВСDH
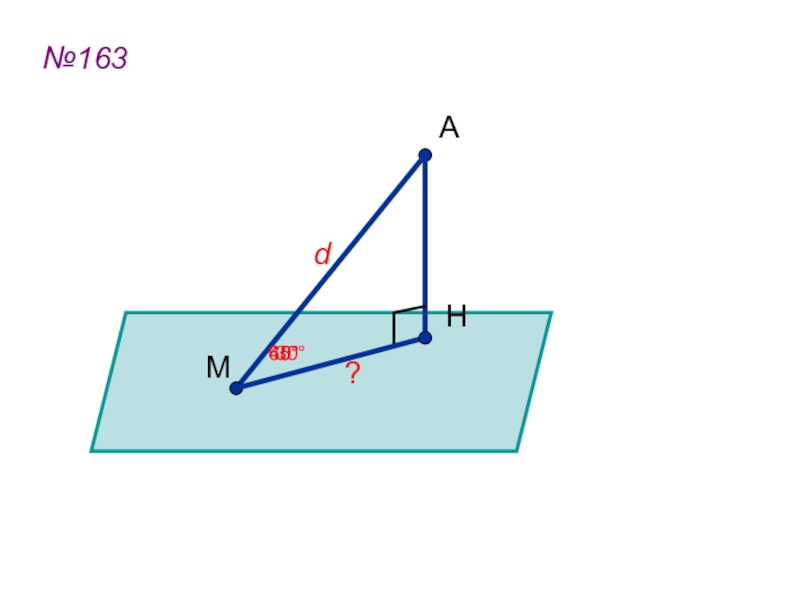
- 41. №163АМdH?45°60°30°
- 42. Урок 6Решение задач по теме
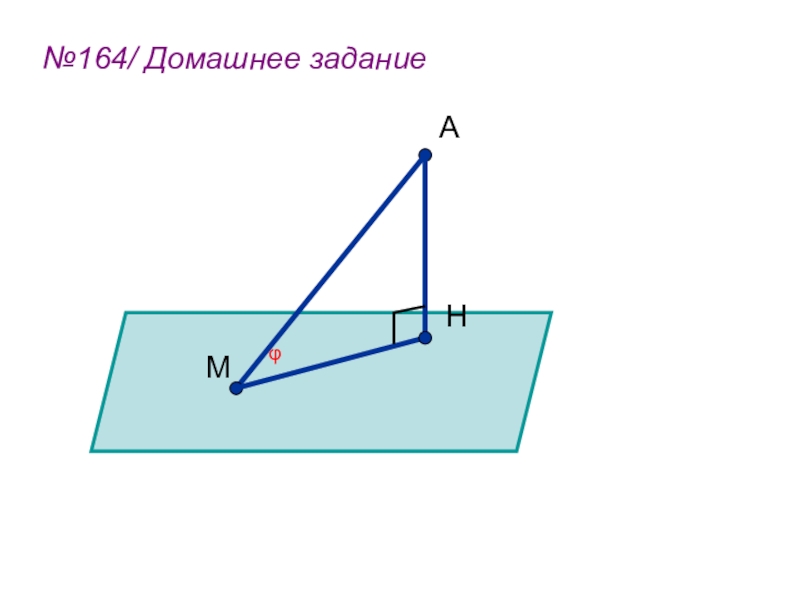
- 43. №164/ Домашнее заданиеАМHφ φ = 60°
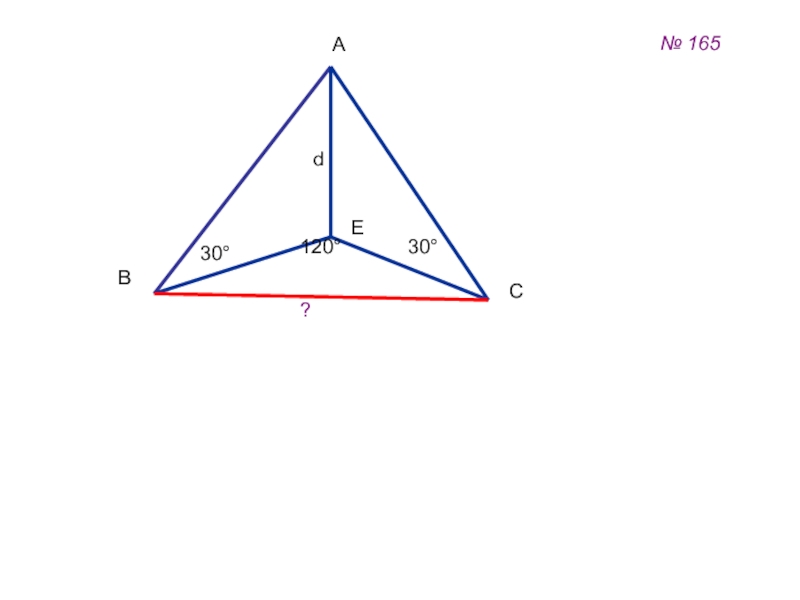
- 44. АBCE30°30°?d120°№ 165
- 45. 1.Найти угол между B1D и (АВС), между
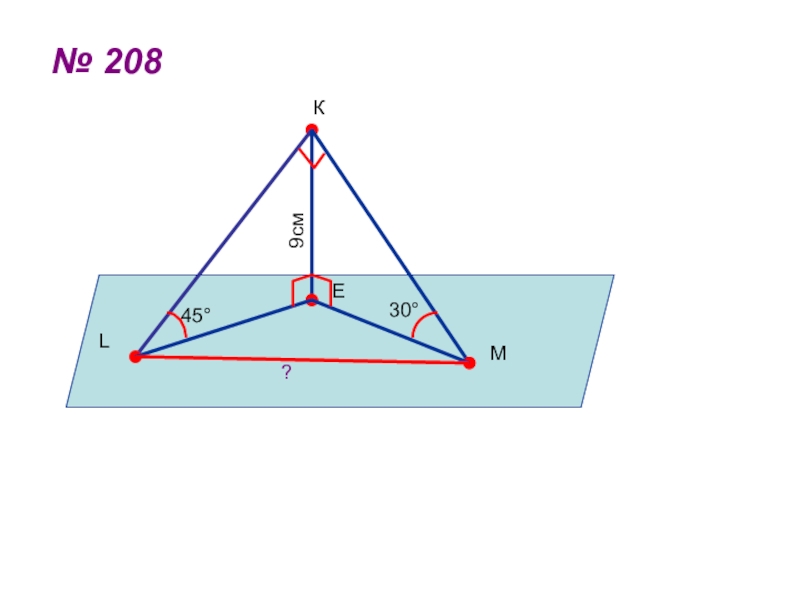
- 46. № 208КLME45°30°?9см
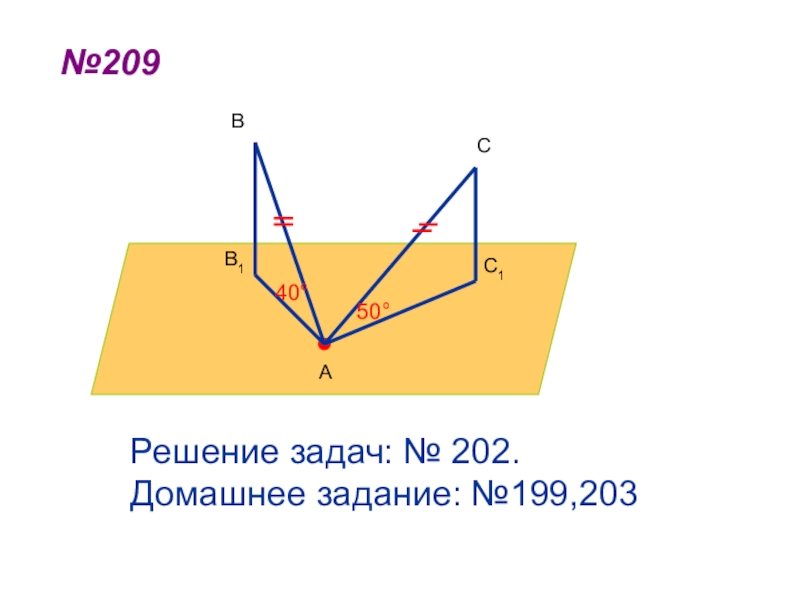
- 47. №209АВСС1В140°50°Решение задач: № 202.Домашнее задание: №199,203
- 48. Урок 7Решение задач по темам
- 49. Проверка домашнего задания№199SMABC
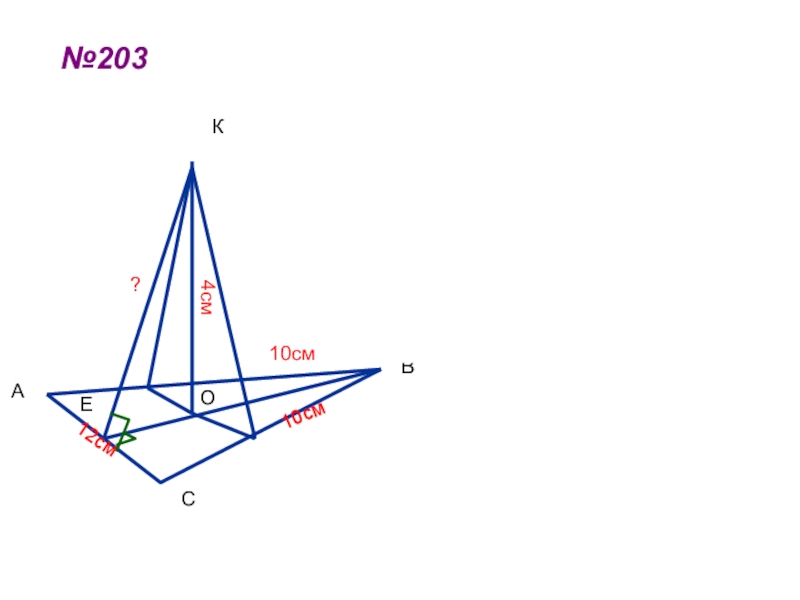
- 50. №203АВСЕКО?10см10см12см4см
- 51. 1.В ∆АВС: AD = BD = CD,
- 52. 5.В ∆АВС : DO (ABC),
- 53. Решение задач: №202,204. Домашнее задание: №206,207.
- 54. Задачи по теме "Расстояние
- 55. 3.В прямоугольном треугольнике катет равен а, противолежащий
- 56. Задачи по теме " Угол между прямой и плоскостью"
- 57. 3.АА1 (АВС). Найти угол
- 58. 5.Через сторону квадрата, площадь которого равна 4,
Слайд 2Презентация по геометрии учителя математики МКОУ СОШ №1 пгт. Палана Камчатский край Учебник геометрии 10 –
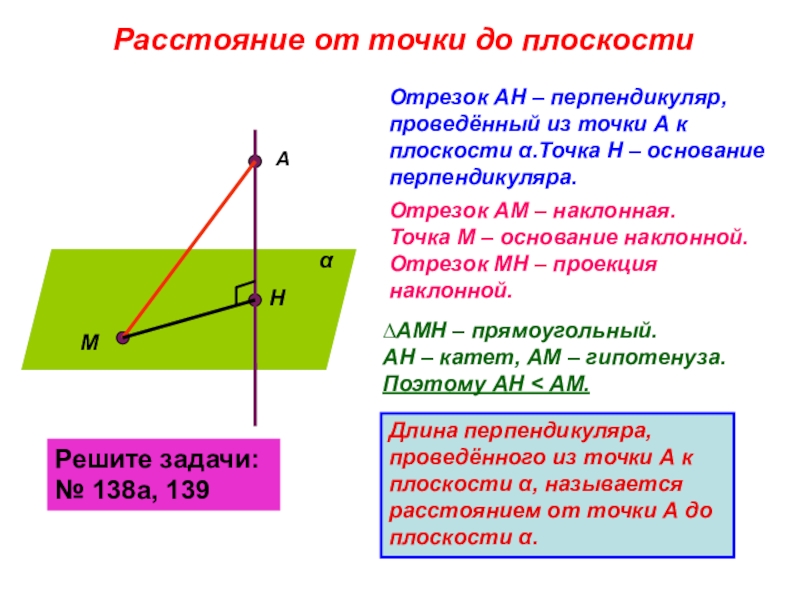
Слайд 4Расстояние от точки до плоскости
α
А
Н
М
Отрезок АН – перпендикуляр, проведённый из точки
Отрезок АМ – наклонная. Точка М – основание наклонной. Отрезок МН – проекция наклонной.
∆АМН – прямоугольный. АН – катет, АМ – гипотенуза. Поэтому АН < АМ.
Длина перпендикуляра, проведённого из точки А к плоскости α, называется расстоянием от точки А до плоскости α.
Решите задачи: № 138а, 139
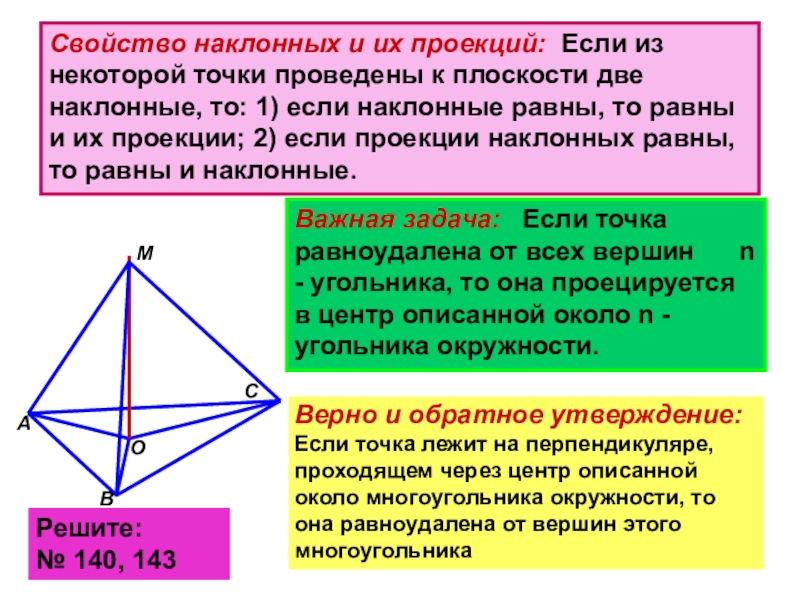
Слайд 5Свойство наклонных и их проекций: Если из некоторой точки проведены к
А
В
С
М
O
Важная задача: Если точка равноудалена от всех вершин n - угольника, то она проецируется в центр описанной около n - угольника окружности.
Верно и обратное утверждение: Если точка лежит на перпендикуляре, проходящем через центр описанной около многоугольника окружности, то она равноудалена от вершин этого многоугольника
Решите: № 140, 143
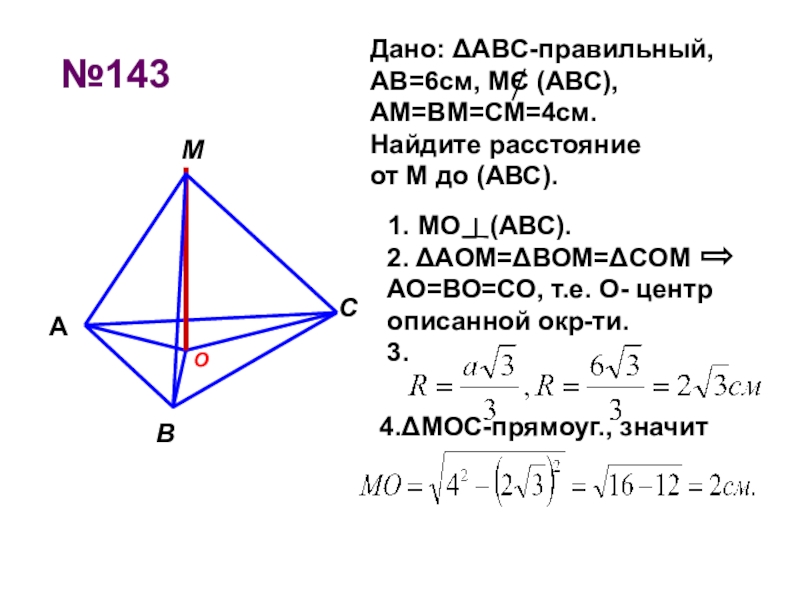
Слайд 6№143
1. МО (АВС).
4.ΔMOC-прямоуг., значит
В
С
М
O
А
Дано: ΔABC-правильный, АВ=6см, МЄ (АВС), АМ=ВМ=СМ=4см. Найдите расстояние от М до (АВС).
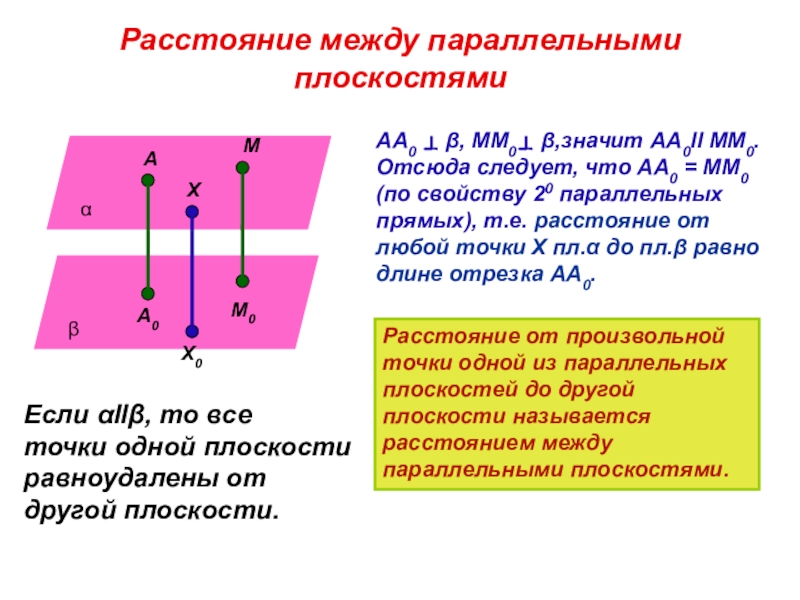
Слайд 7Расстояние между параллельными плоскостями
А
М
А0
М0
Х
Х0
α
β
АА0 β, ММ0 β,значит
Расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями.
Если αllβ, то все точки одной плоскости равноудалены от другой плоскости.
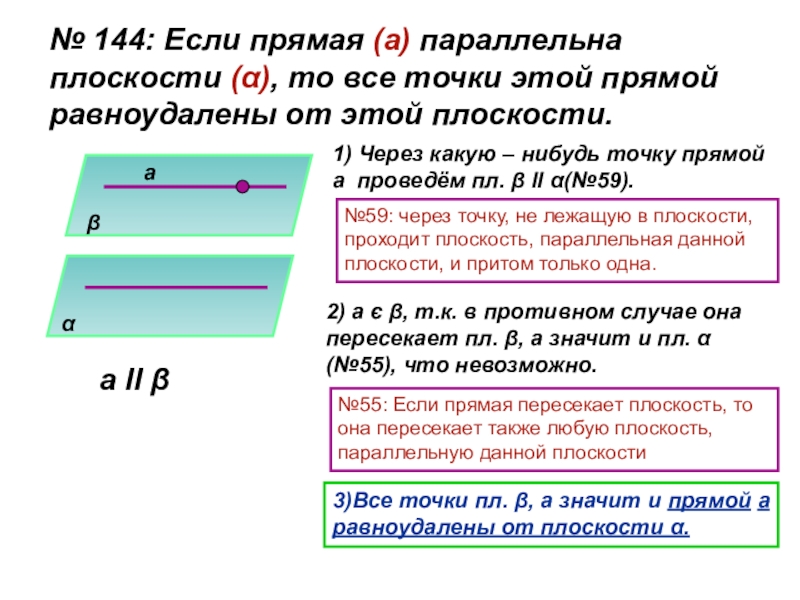
Слайд 8№ 144: Если прямая (а) параллельна плоскости (α), то все точки
α
а
β
1) Через какую – нибудь точку прямой а проведём пл. β ll α(№59).
№59: через точку, не лежащую в плоскости, проходит плоскость, параллельная данной плоскости, и притом только одна.
2) а є β, т.к. в противном случае она пересекает пл. β, а значит и пл. α (№55), что невозможно.
№55: Если прямая пересекает плоскость, то она пересекает также любую плоскость, параллельную данной плоскости
3)Все точки пл. β, а значит и прямой а равноудалены от плоскости α.
а ll β
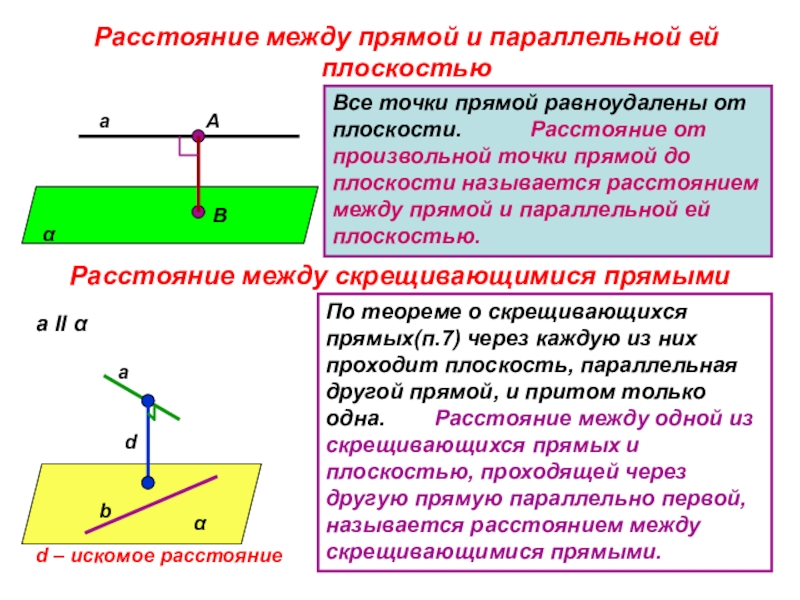
Слайд 9Расстояние между прямой и параллельной ей плоскостью
а
α
А
В
Все точки прямой равноудалены от
Расстояние между скрещивающимися прямыми
а
По теореме о скрещивающихся прямых(п.7) через каждую из них проходит плоскость, параллельная другой прямой, и притом только одна. Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
b
α
а ll α
d
d – искомое расстояние
Слайд 10Решение задач: №138а,139,140,143
Домашнее задание:
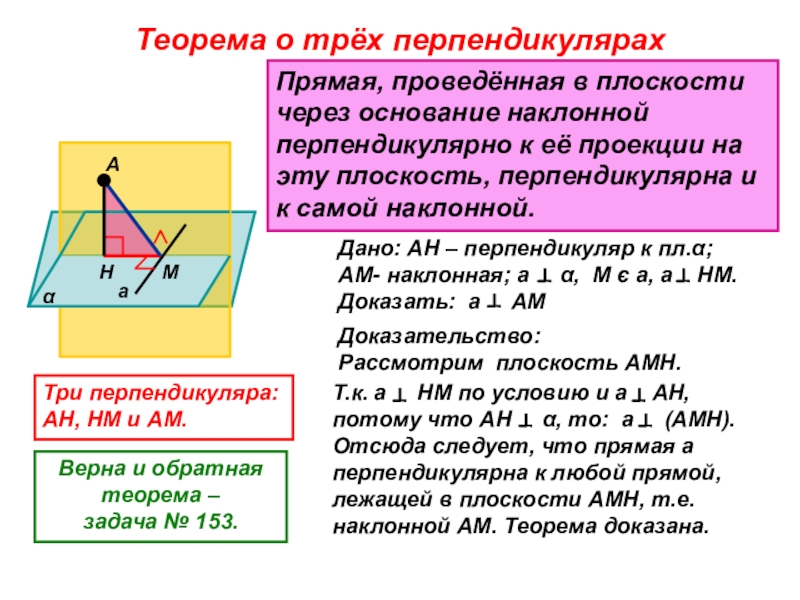
Слайд 14Теорема о трёх перпендикулярах
α
А
Н
М
а
Прямая, проведённая в плоскости через основание наклонной перпендикулярно
Дано: АН – перпендикуляр к пл.α; АМ- наклонная; а α, М є а, а НМ. Доказать: а АМ
Доказательство: Рассмотрим плоскость АМН.
Т.к. а НМ по условию и а АН, потому что АН α, то: а (АМН). Отсюда следует, что прямая а перпендикулярна к любой прямой, лежащей в плоскости АМН, т.е. наклонной АМ. Теорема доказана.
Три перпендикуляра: АН, НМ и АМ.
Верна и обратная теорема – задача № 153.
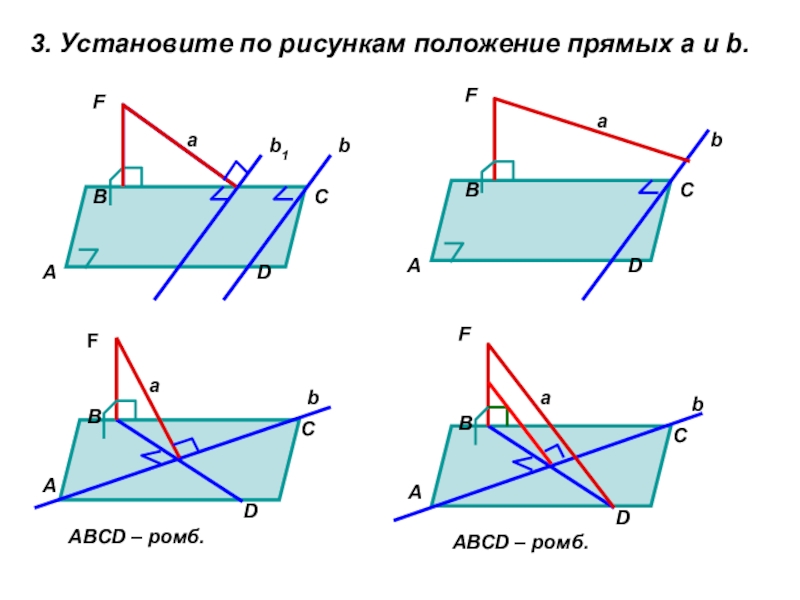
Слайд 153. Установите по рисункам положение прямых а и b.
А
В
С
D
b
а
F
b1
А
В
F
a
C
D
b
A
B
F
a
b
C
D
ABCD –
A
B
F
a
b
C
D
ABCD – ромб.
Слайд 21
А
В
С
а
а1
1.
Верно ли утверждение: « Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной
А
Н
М
а
2.
Верно ли утверждение: « Если прямая перпендикулярна проекции наклонной, то эта прямая перпендикулярна и самой наклонной»?
Верно.
Неверно.
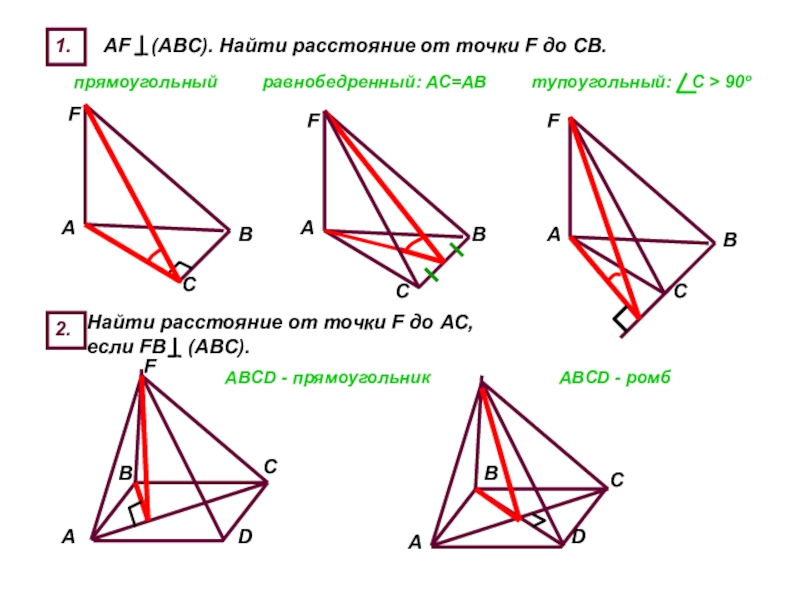
Слайд 251.
AF (ABC). Найти расстояние от точки F до СВ.
прямоугольный
А
В
С
F
A
B
C
F
A
B
C
F
2.
Найти расстояние от точки F до АС, если FB (ABC).
ABCD - прямоугольник
АВСD - ромб
А
В
С
D
F
A
B
C
D
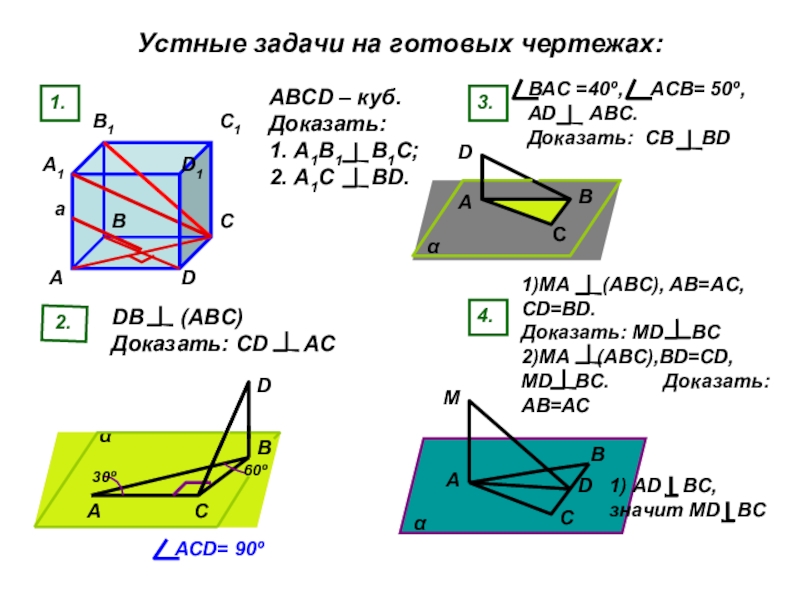
Слайд 26Устные задачи на готовых чертежах:
1.
А
А1
В
В1
С
С1
D
АВСD – куб. Доказать: 1.
а
D1
A
B
C
D
α
30º
60º
DB (ABC) Доказать: CD AC
2.
3.
D
A
B
C
BAC =40º, ACB= 50º, AD ABC. Доказать: CB BD
4.
α
M
A
B
D
C
α
1)MA (ABC), AB=AC, CD=BD. Доказать: MD BC 2)MA (ABC),BD=CD, MD BC. Доказать: АВ=АС
АСD= 90º
1) AD BC, значит MD BC
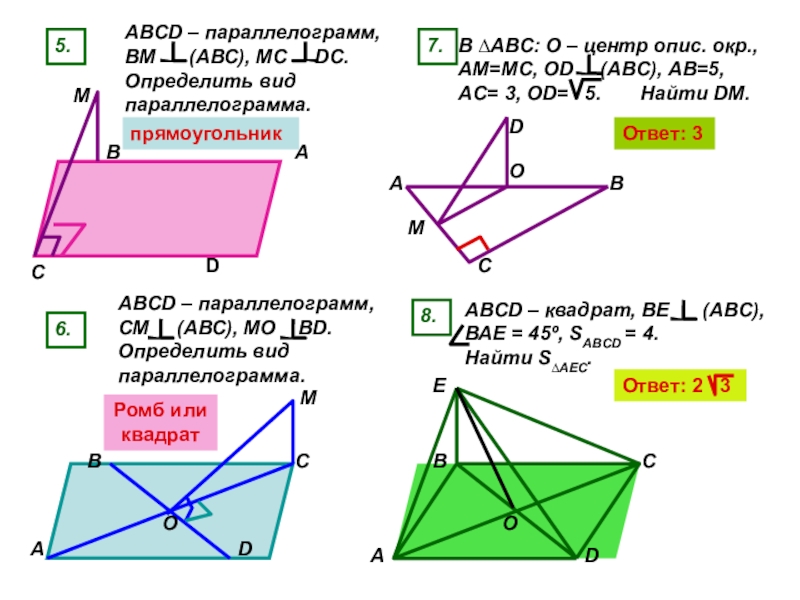
Слайд 275.
A
B
C
D
ABCD – параллелограмм, ВМ (АВС), МС
6.
М
ABCD – параллелограмм, СМ (АВС), МО ВD. Определить вид параллелограмма.
А
В
С
D
O
M
7.
A
O
D
B
C
M
В ∆АВС: О – центр опис. окр., АМ=МС, ОD (ABC), AB=5, AC= 3, OD= 5. Найти DM.
8.
A
B
C
D
E
ABCD – квадрат, ВЕ (АВС), ВАЕ = 45º, SABCD = 4. Hайти S∆AEC.
прямоугольник
Ромб или квадрат
Ответ: 3
О
Ответ: 2 3
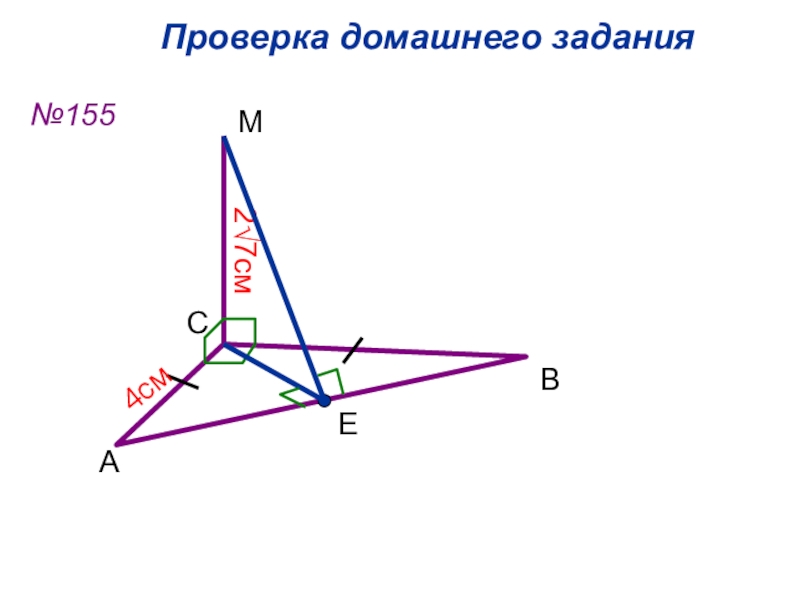
Слайд 30 Проверка домашнего задания
№155
С
М
А
В
4см
2√7см
Е
АЕ=ВЕ=СЕ=2√2см, МЕ2=(2√7)2+(2√2)2= =28+8=36, МЕ = 6(см)
Слайд 31№159
В
С
D
А
М
Е
1) МЕ ІІAD,DEІІΑМ; 2) AM AD(ттп)
3)AD MB,AD AB AD (AMB); 4)тогда МЕ (АМВ)
ттп
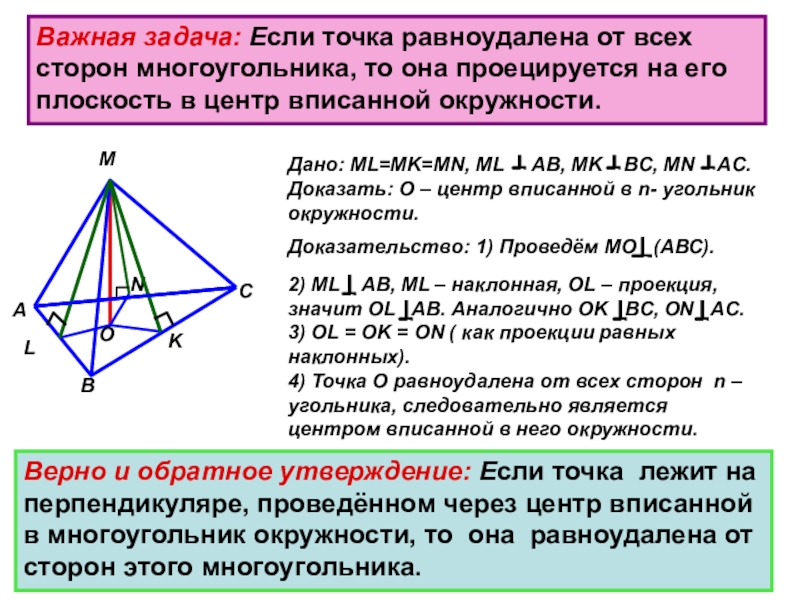
Слайд 32Важная задача: Если точка равноудалена от всех сторон многоугольника, то она
М
L
A
B
K
C
N
O
Дано: МL=MK=MN, ML AB, MK BC, MN AC. Доказать: О – центр вписанной в n- угольник окружности.
Доказательство: 1) Проведём МО (АВС).
2) ML AB, ML – наклонная, OL – проекция, значит OL AB. Аналогично OK BC, ON AC. 3) OL = OK = ON ( как проекции равных наклонных). 4) Точка О равноудалена от всех сторон n – угольника, следовательно является центром вписанной в него окружности.
Верно и обратное утверждение: Если точка лежит на перпендикуляре, проведённом через центр вписанной в многоугольник окружности, то она равноудалена от сторон этого многоугольника.
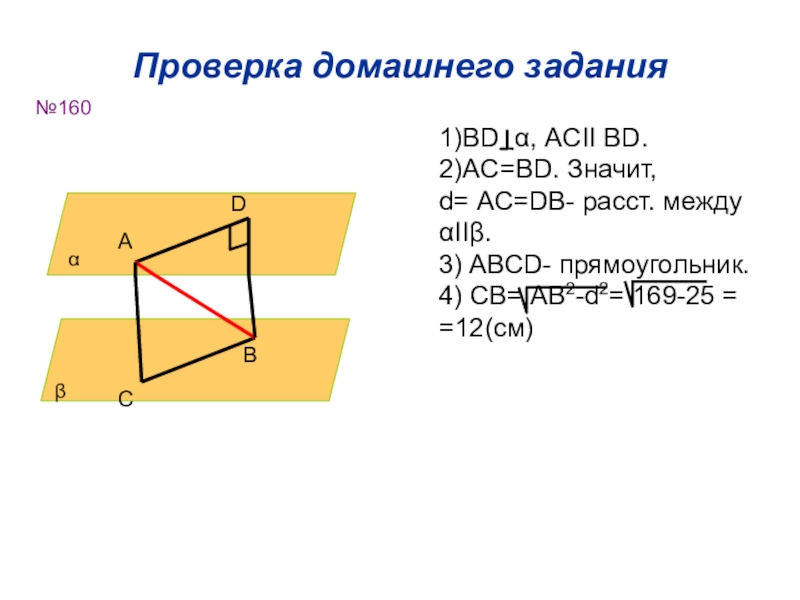
Слайд 35Проверка домашнего задания
№160
α
β
А
D
C
B
1)ВD α, ACІІ BD.
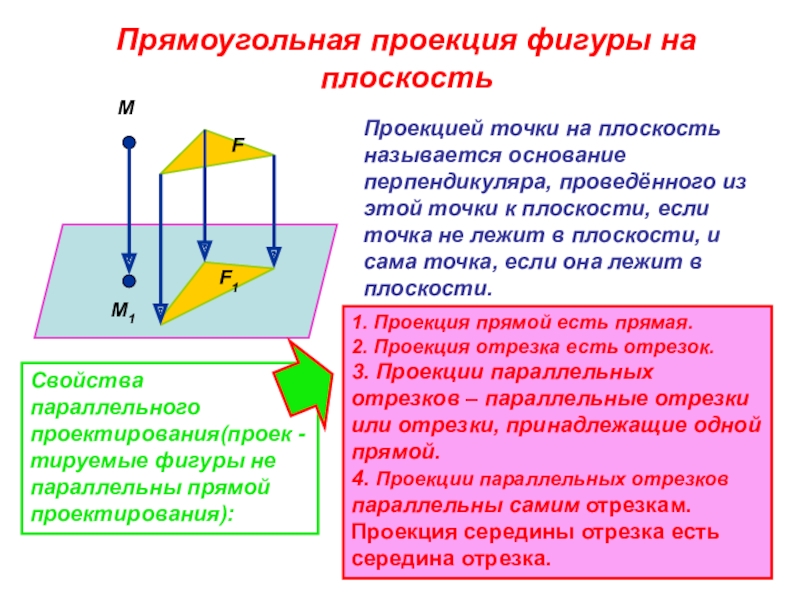
Слайд 37Прямоугольная проекция фигуры на плоскость
М
М1
F
F1
Проекцией точки на плоскость называется основание перпендикуляра,
Свойства параллельного проектирования(проек -тируемые фигуры не параллельны прямой проектирования):
1. Проекция прямой есть прямая. 2. Проекция отрезка есть отрезок. 3. Проекции параллельных отрезков – параллельные отрезки или отрезки, принадлежащие одной прямой. 4. Проекции параллельных отрезков параллельны самим отрезкам. Проекция середины отрезка есть середина отрезка.
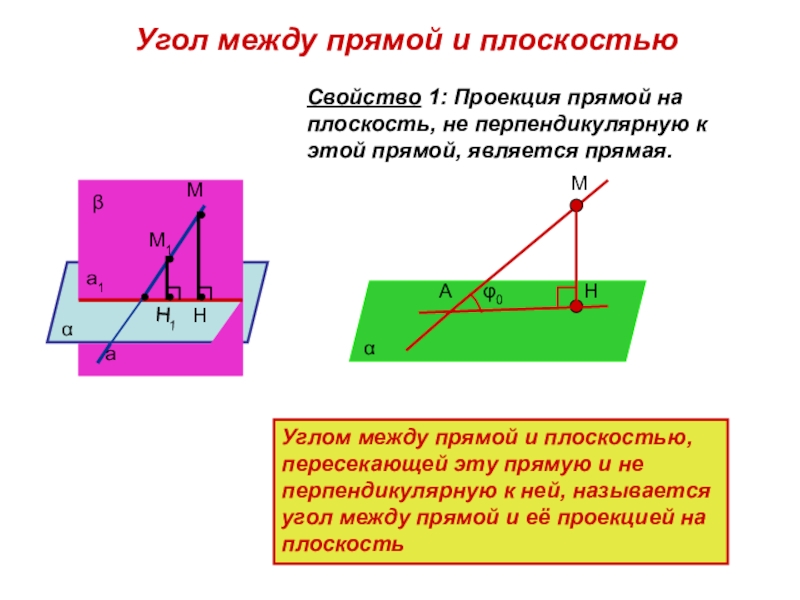
Слайд 38Свойство 1: Проекция прямой на плоскость, не перпендикулярную к этой прямой,
Угол между прямой и плоскостью
α
β
а
а1
М
М1
Н1
Н
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней, называется угол между прямой и её проекцией на плоскость
φ0
М
А
Н
α
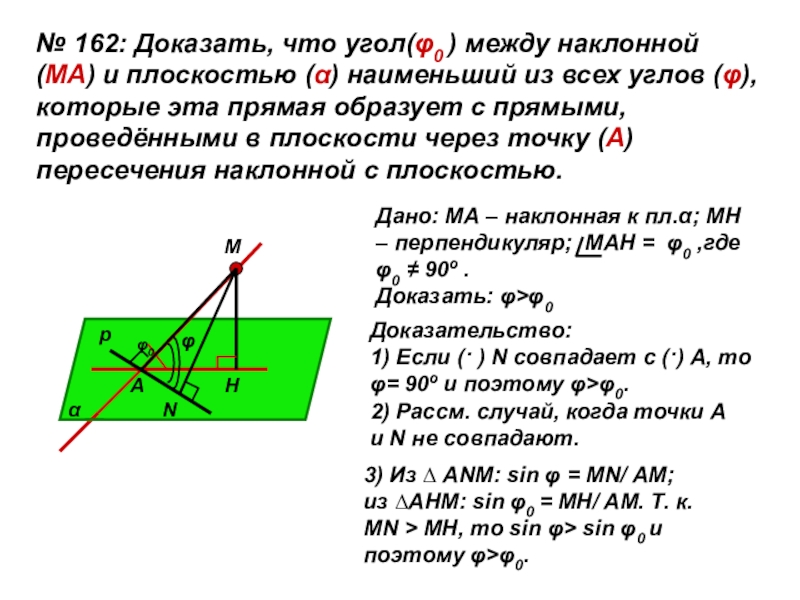
Слайд 39№ 162: Доказать, что угол(φ0 ) между наклонной (МА) и плоскостью
φ0
φ
М
Н
N
А
р
α
Дано: МА – наклонная к пл.α; МН – перпендикуляр; МАН = φ0 ,где φ0 ≠ 90º . Доказать: φ>φ0
Доказательство: 1) Если (· ) N совпадает с (·) А, то φ= 90º и поэтому φ>φ0.
2) Рассм. случай, когда точки А и N не совпадают.
3) Из ∆ АNM: sin φ = MN/ AM; из ∆АНМ: sin φ0 = MH/ AM. Т. к. МN > MH, то sin φ> sin φ0 и поэтому φ>φ0.
Слайд 451.
Найти угол между B1D и (АВС), между B1D и (DD1C), где
А
С
D
A1
B1
C1
прямоугольник параллелограмм
А
В
С
D
A1
B1
C1
D1
В1
D1
E
2.
BB1 (ABC). Найти угол между ВС1 и (АА1В1).
А
В
С
А1
С1
В1
А
В
С
А1
С1
В1
А
С
В
А1
С1
В1
∆АВС –равносторонний; прямоугольный: В = 90º; тупоугольный: В >90º
D
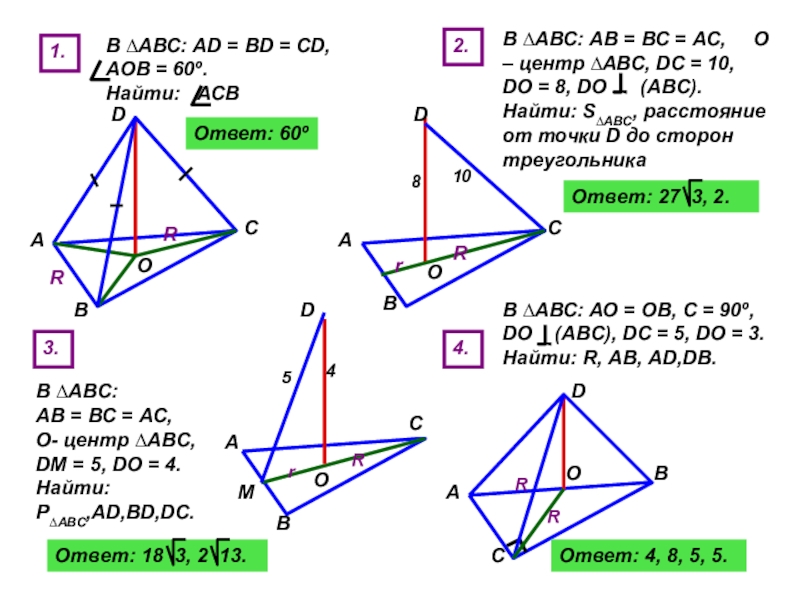
Слайд 511.
В ∆АВС: AD = BD = CD, AOB =
А
В
С
D
O
Ответ: 60º
2.
В ∆АВС: АВ = ВС = АС, О – центр ∆АВС, DC = 10, DO = 8, DO (ABC). Найти: S∆ABC, расстояние от точки D до сторон треугольника
А
В
C
D
O
8
10
R
R
R
r
Ответ: 27 3, 2.
3.
В ∆АВС: АВ = ВС = АС, О- центр ∆АВС, DM = 5, DO = 4. Найти: Р∆АВС,AD,BD,DC.
A
B
C
D
O
M
5
4
r
R
Ответ: 18 3, 2 13.
4.
В ∆АВС: АО = ОВ, С = 90º, DO (ABC), DC = 5, DO = 3. Найти: R, АВ, AD,DB.
D
O
A
B
C
R
R
Ответ: 4, 8, 5, 5.
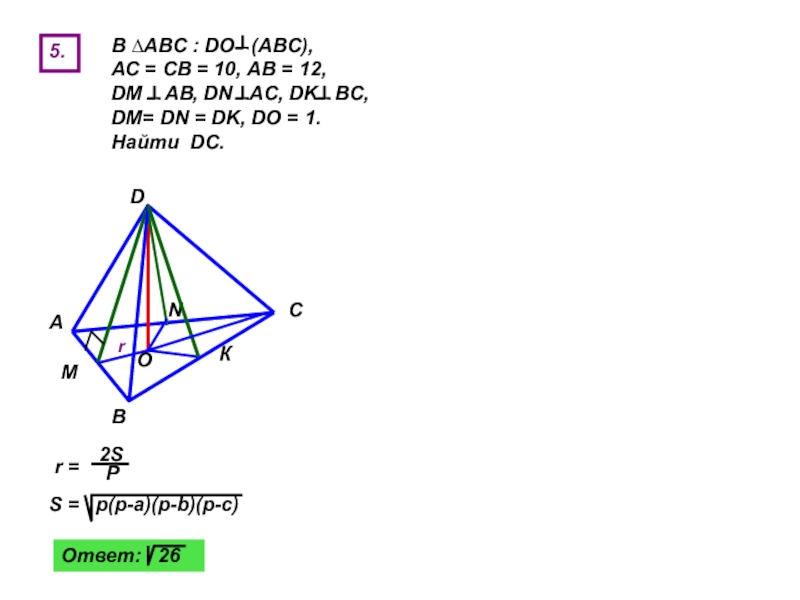
Слайд 525.
В ∆АВС : DO (ABC), АС =
А
М
В
К
С
N
O
D
r
r =
2S
P
S = p(p-a)(p-b)(p-c)
Ответ: 26
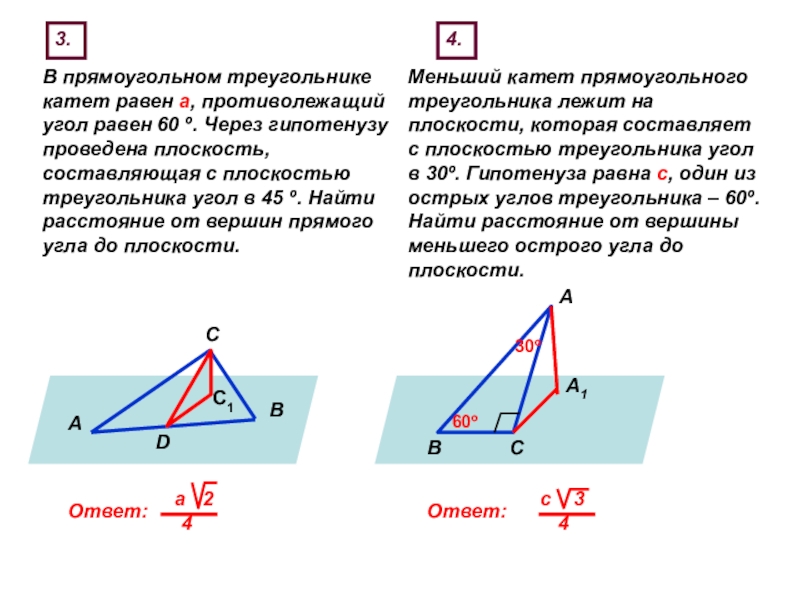
Слайд 553.
В прямоугольном треугольнике катет равен а, противолежащий угол равен 60 º.
А
В
С
С1
D
Ответ:
а 2
4
4.
Меньший катет прямоугольного треугольника лежит на плоскости, которая составляет с плоскостью треугольника угол в 30º. Гипотенуза равна с, один из острых углов треугольника – 60º. Найти расстояние от вершины меньшего острого угла до плоскости.
А
А1
В
С
60º
30º
Ответ:
с 3
4
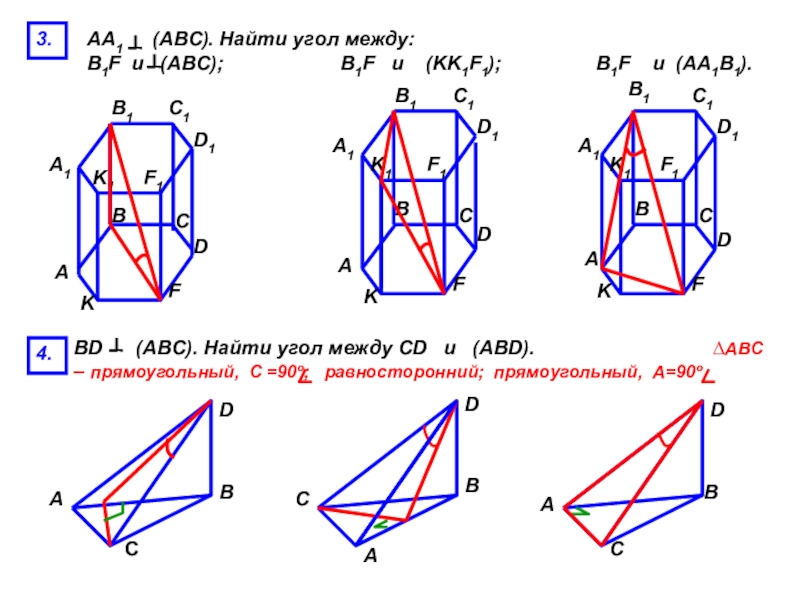
Слайд 573.
АА1 (АВС). Найти угол между:
А
В
С
D
F
K
A1
B1
С1
D1
F1
K1
A
B
C
D
F
K
A1
B1
C1
D1
F1
K1
A
B
C
D
F
K
A1
B1
C1
D1
F1
K1
4.
BD (ABC). Найти угол между CD и (ABD). ∆ABC – прямоугольный, С =90º; равносторонний; прямоугольный, А=90º
А
В
С
D
C
В
A
D
A
B
C
D
Слайд 585.
Через сторону квадрата, площадь которого равна 4, проведена плоскость. Расстояние от
А
В
С
D
М
Ответ: 60º
6.
Через большее основание прямоугольной трапеции проведена плоскость, составляющая с большей боковой стороной угол в 30º. Меньшее основание отстоит от плоскости на расстояние 8см. Найти периметр трапеции, если известно, что внеё можно вписать окружность, и острый угол равен 60º.
А
В
С
D
C1
E
Ответ: 32 + 16 3