- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Четырехугольники
Содержание
- 1. Презентация по геометрии Четырехугольники
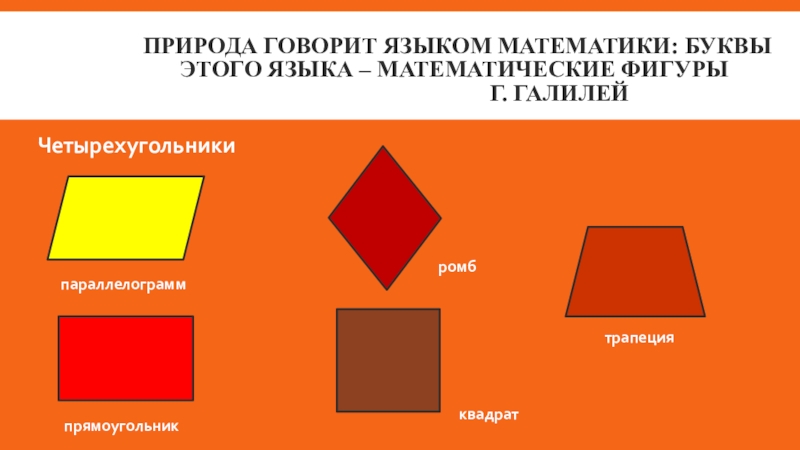
- 2. Природа говорит языком математики: буквы этого языка – математические фигуры Г. Галилей параллелограммпрямоугольникромбквадраттрапецияЧетырехугольники
- 3. Свойства четырехугольниковЕсли у четырехугольника:АВ II CD, AD
- 4. Математический диктант1) Четырёхугольник, у которого диагонали пересекаются
- 5. Математический диктантОтветы: параллелограммомтрапецией прямоугольникомдиагональюквадратом основаниями периметром верны
- 6. Решение задач по готовым чертежам4025АВСDДано:ABCD- параллелограммВАС =
- 7. Решение задач по готовым чертежам55АВСDДано:ABCD- ромбCBD =
- 8. ЗадачаВ трапеции ABCD угол А равен 400.
- 9. Домашнее заданиеДополнительные задачи № 425, 436Печатная тетрадь №23, 24Спасибо за работу!
Слайд 2Природа говорит языком математики: буквы этого языка – математические фигуры Г.
параллелограмм
прямоугольник
ромб
квадрат
трапеция
Четырехугольники
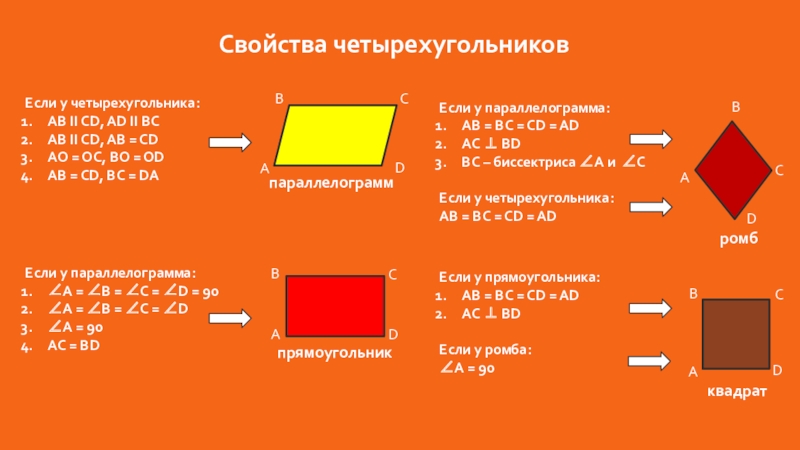
Слайд 3Свойства четырехугольников
Если у четырехугольника:
АВ II CD, AD II BC
AB II CD,
AO = OC, BO = OD
AB = CD, BC = DA
параллелограмм
Если у параллелограмма:
A = B = C = D = 90
A = B = C = D
A = 90
AC = BD
прямоугольник
Если у параллелограмма:
AB = BC = CD = AD
AC BD
ВС – биссектриса A и C
Если у четырехугольника:
AB = BC = CD = AD
ромб
Если у прямоугольника:
AB = BC = CD = AD
AC BD
Если у ромба:
A = 90
квадрат
А
А
А
А
В
В
В
В
С
С
С
С
D
D
D
D
Слайд 4Математический диктант
1) Четырёхугольник, у которого диагонали пересекаются и точкой пересечения делятся
2) Четырёхугольник, у которого только две стороны параллельны, называется…
3) Параллелограмм, у которого диагонали равны, является…
4)Отрезок, соединяющий две несоседние вершины n-угольника, называется…
5) Если диагонали ромба равны, то он является ….
6) Параллельные стороны трапеции называются ……
7) Сумма длин всех сторон n-угольника называется ….
8) Какие из следующих утверждений верны?
а) Если сумма углов, прилежащих к любой стороне четырехугольника, равна 180, то он является параллелограммом.
б) Четырехугольник, противолежащие углы которого равны, является параллелограммом.
в) Всякий четырехугольник, имеющий две пары равных сторон, является параллелограммом.
г) Любой четырехугольник, у которого есть равные стороны и равные углы, является параллелограммом.
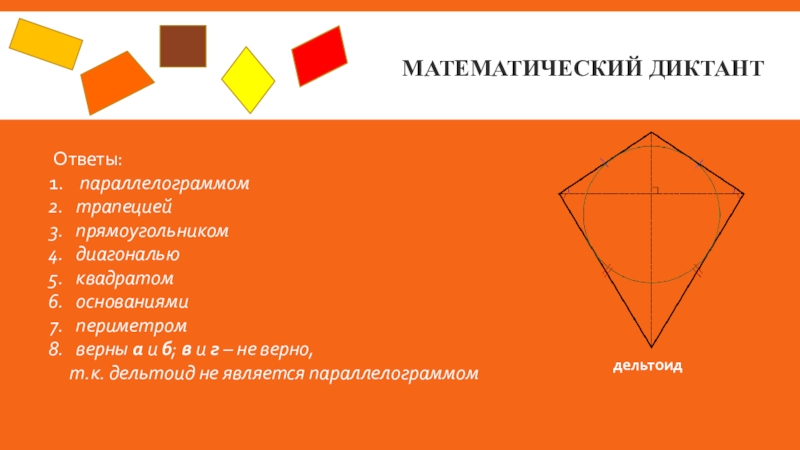
Слайд 5Математический диктант
Ответы:
параллелограммом
трапецией
прямоугольником
диагональю
квадратом
основаниями
периметром
верны а и б; в
т.к. дельтоид не является параллелограммом
дельтоид
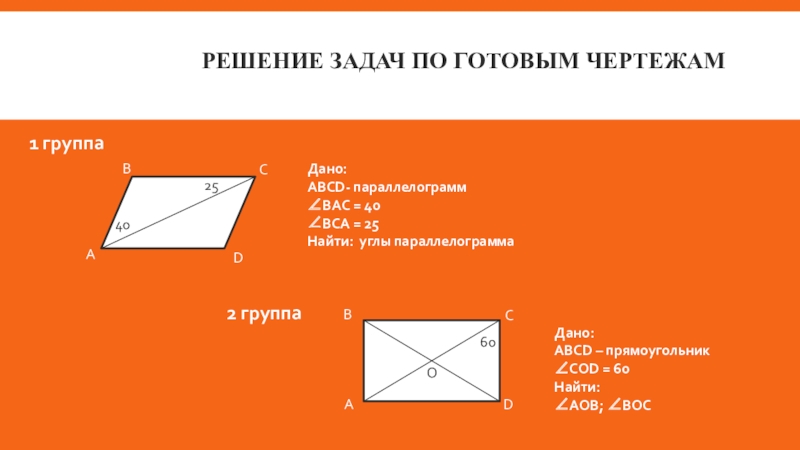
Слайд 6Решение задач по готовым чертежам
40
25
А
В
С
D
Дано:
ABCD- параллелограмм
ВАС = 40
ВСА = 25
Найти: углы
1 группа
2 группа
60
А
В
С
D
О
Дано:
ABCD – прямоугольник
СОD = 60
Найти:
АОВ; ВОС
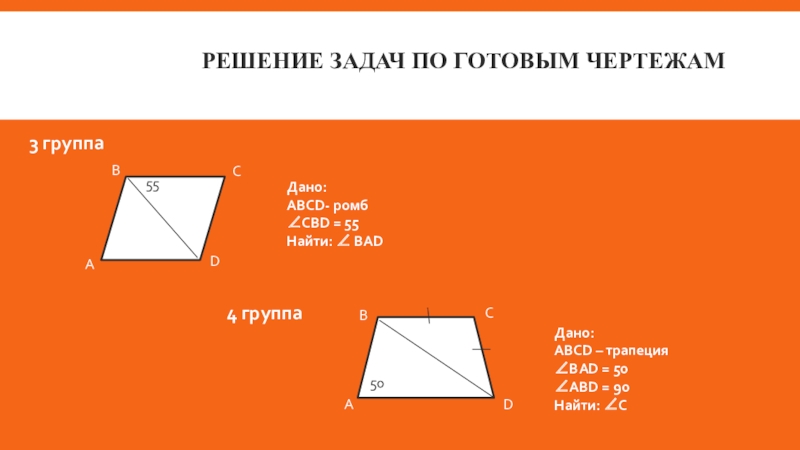
Слайд 7Решение задач по готовым чертежам
55
А
В
С
D
Дано:
ABCD- ромб
CBD = 55
Найти: BAD
3
4 группа
А
В
С
D
Дано:
ABCD – трапеция
ВАD = 50
АВD = 90
Найти: С
50
Слайд 8Задача
В трапеции ABCD угол А равен 400. Из угла В проведен
А
В
С
D
Е
40
75