- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 8 класса на тему Диаметры. ходы и дуги окружности
Содержание
- 1. Презентация по геометрии 8 класса на тему Диаметры. ходы и дуги окружности
- 2. Диаметр, перпендикулярный к хордеДиаметр, перпендикулярный к хорде,
- 3. Равные хордыХорды, равноудалённые от центра окружностиЕсли хорды
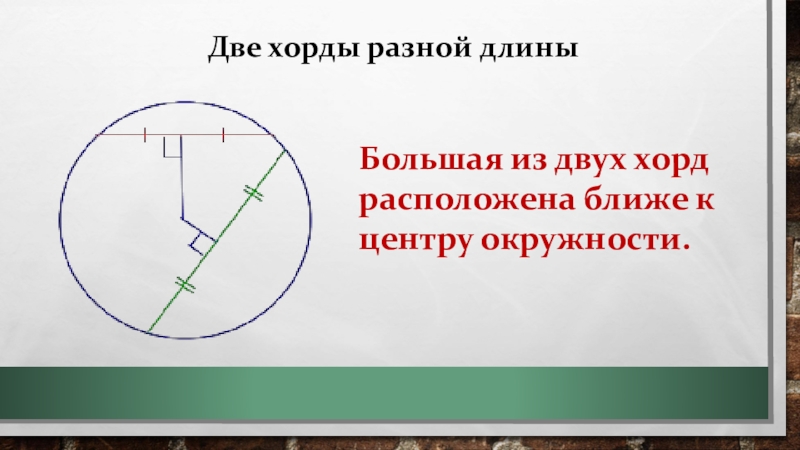
- 4. Две хорды разной длиныБольшая из двух хорд расположена ближе к центру окружности.
- 5. Равные дугиЕсли дуги равны, то равны и
- 6. Параллельные хордыДуги, заключённые между параллельными хордами, равны.
- 7. Если две хорды пересекаются, то произведения длин
- 8. Касательные, проведённые к окружности из одной точкиЕсли
- 9. Касательная и секущая, проведённые к окружности из
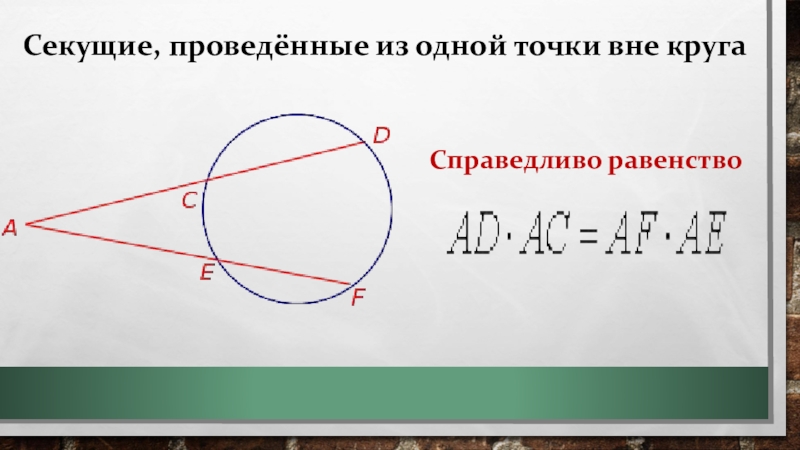
- 10. Секущие, проведённые из одной точки вне кругаСправедливо равенство
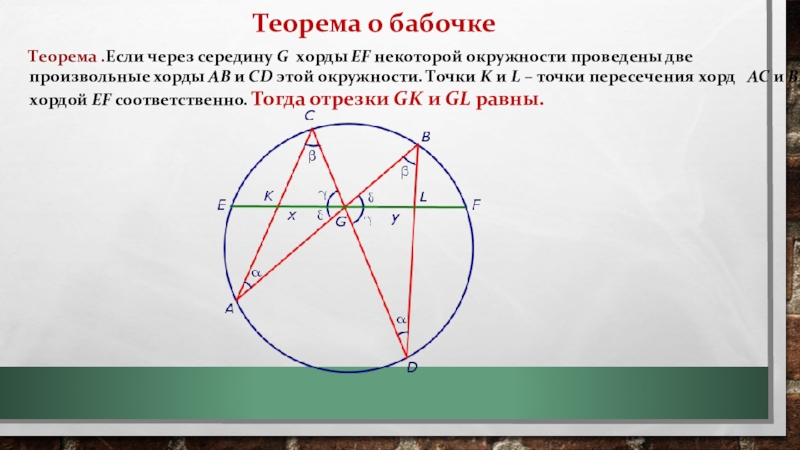
- 11. Теорема о бабочкеТеорема .Если через середину G хорды EF некоторой
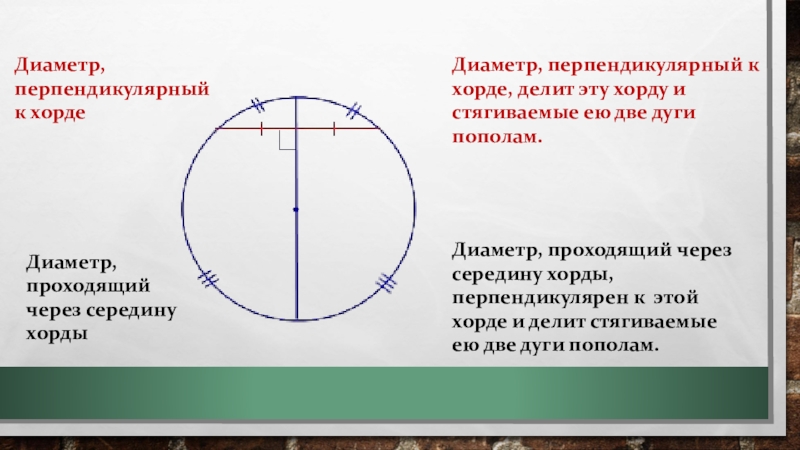
Диаметр, перпендикулярный к хордеДиаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.Диаметр, проходящий через середину хордыДиаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Слайд 2Диаметр, перпендикулярный к хорде
Диаметр, перпендикулярный к хорде, делит эту хорду и
стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
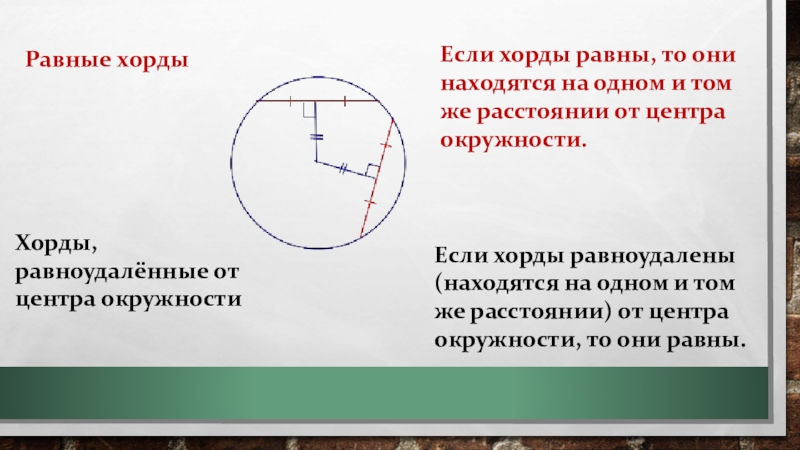
Слайд 3Равные хорды
Хорды, равноудалённые от центра окружности
Если хорды равны, то они находятся на
одном и том же расстоянии от центра окружности.
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
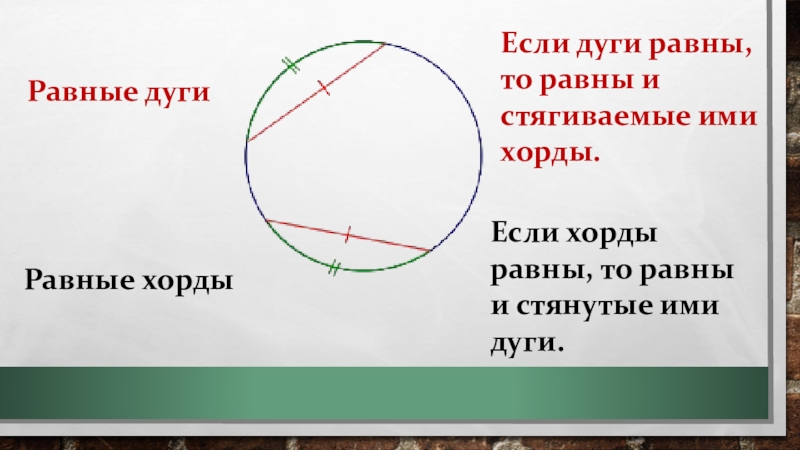
Слайд 5Равные дуги
Если дуги равны, то равны и стягиваемые ими хорды.
Равные хорды
Если
хорды равны, то равны и стянутые ими дуги.
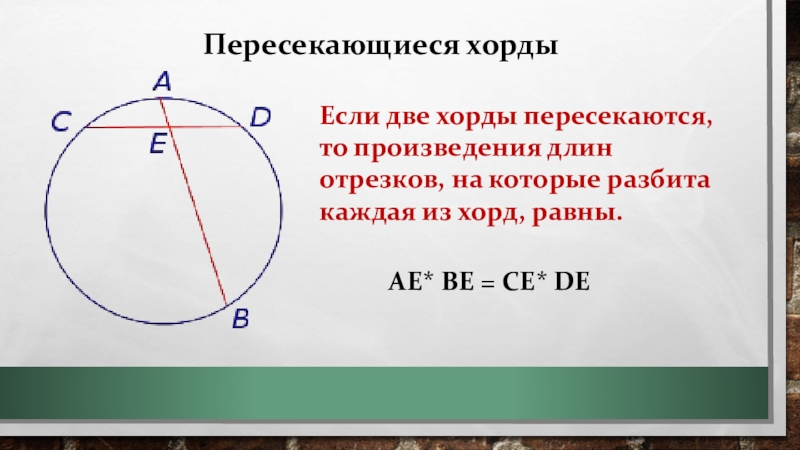
Слайд 7Если две хорды пересекаются, то произведения длин отрезков, на которые разбита
каждая из хорд, равны.
Пересекающиеся хорды
АE* BE = CE* DE
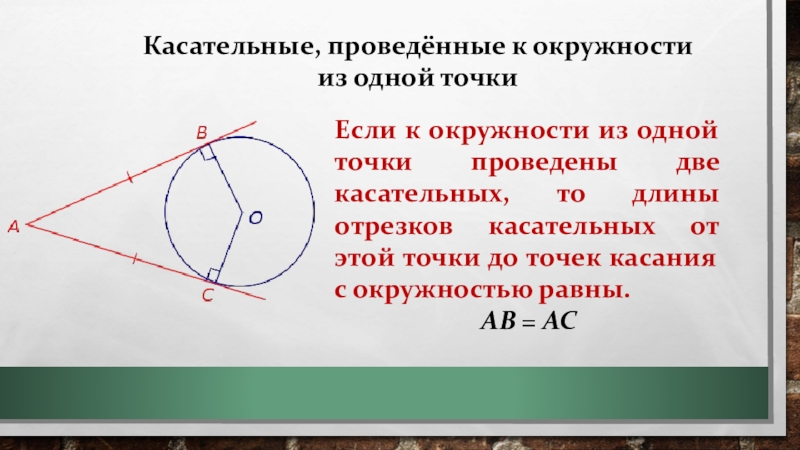
Слайд 8Касательные, проведённые к окружности из одной точки
Если к окружности из одной
точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
AB = AC
AB = AC
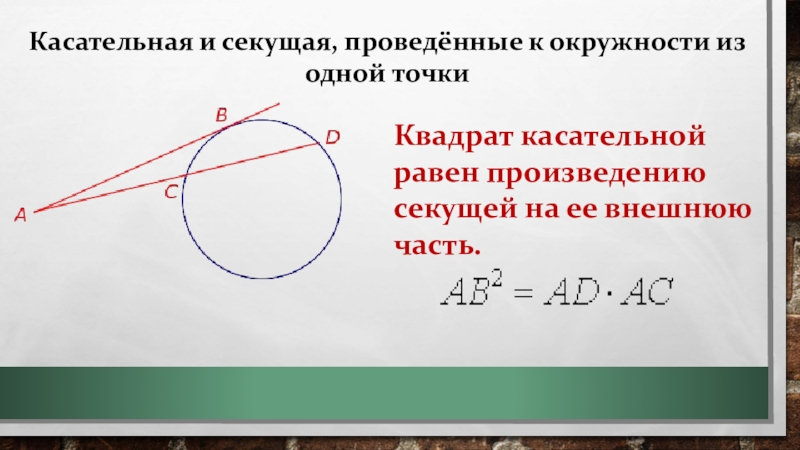
Слайд 9Касательная и секущая, проведённые к окружности из одной точки
Квадрат касательной равен
произведению секущей на ее внешнюю часть.
Слайд 11Теорема о бабочке
Теорема .Если через середину G хорды EF некоторой окружности проведены две произвольные
хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно. Тогда отрезки GK и GL равны.