- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 8 класс Теорема Пифагора
Содержание
- 1. Презентация по геометрии 8 класс Теорема Пифагора
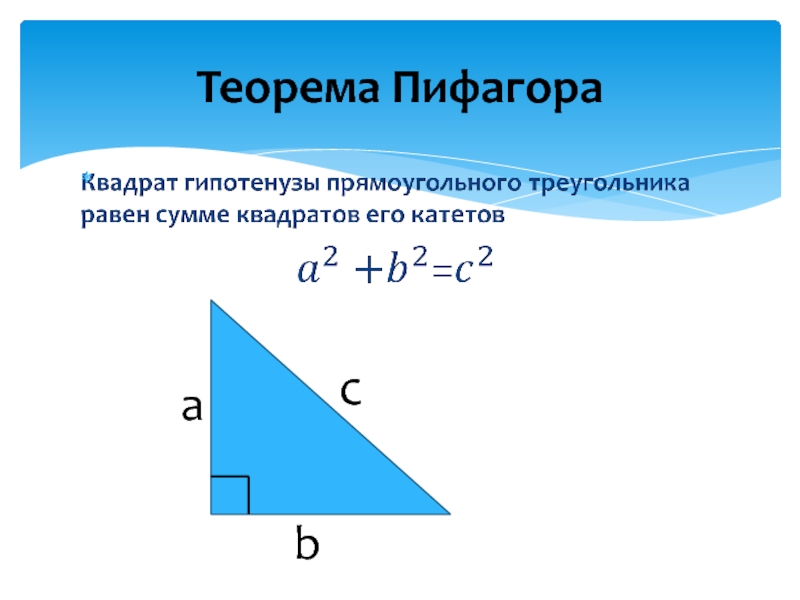
- 2. Теорема Пифагора
- 3. Теорема Пифагораabc
- 4. Мориц Кантор (крупнейший немецкий историк математики) считает,
- 5. Ван-дер-Варден (голландский математик) сделал вывод о большой
- 6. «Принадлежит ли эта формула лично перу Пифагора…,
- 7. В древнекитайской книге Чу-пей говорится о пифагоровом
- 8. «Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик
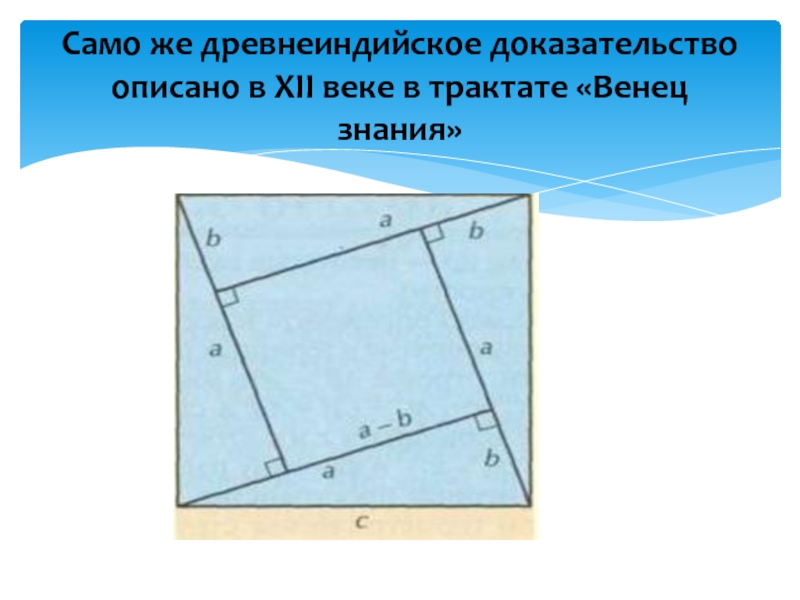
- 9. Само же древнеиндийское доказательство описано в XII веке в трактате «Венец знания»
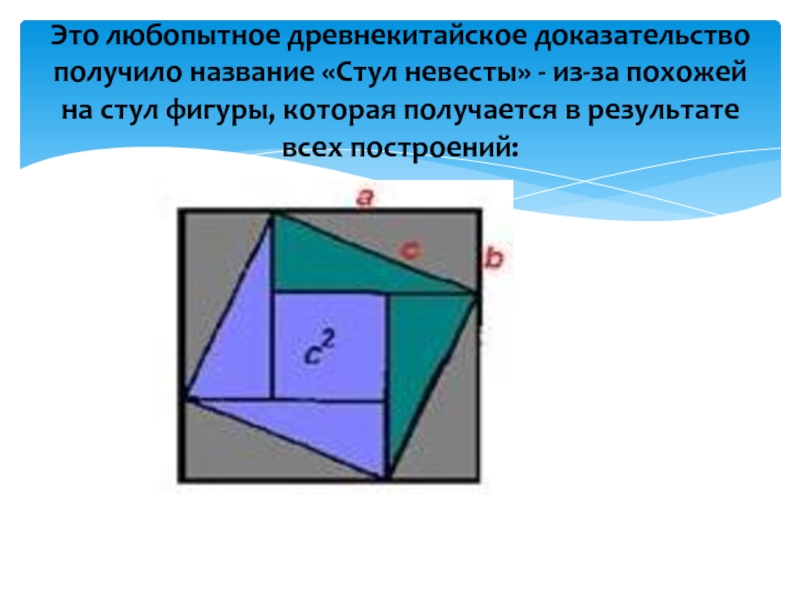
- 10. Это любопытное древнекитайское доказательство получило название «Стул
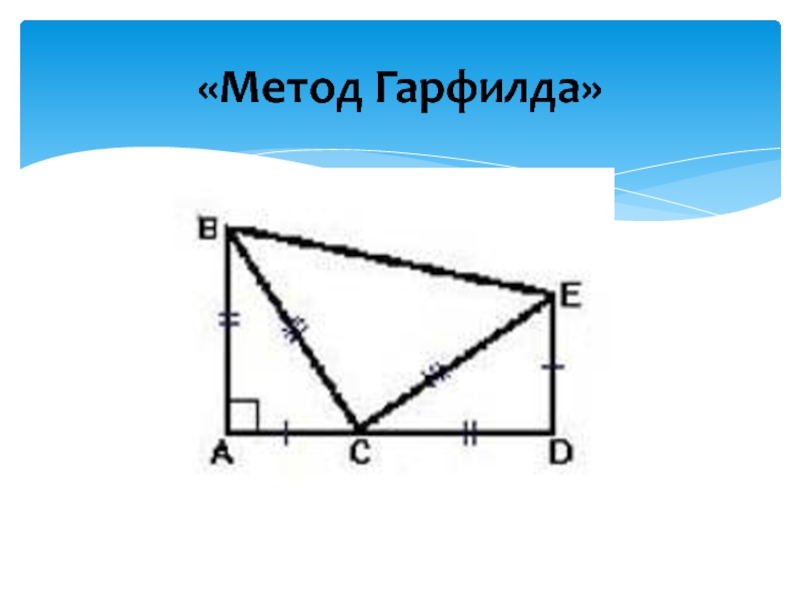
- 11. «Метод Гарфилда»
- 12. Примеры Пифагоровых троек: (3, 4, 5), (6,
- 13. Формулы для вычисления Пифагоровых троек:
Теорема Пифагора
Слайд 4Мориц Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ²
+ 4 ² = 5² было известно уже египтянам ещё около 2300 г. до н. э. во времена царя Аменемхета I (согласно папирусу Берлинского музея). По мнению Кантора, гарпедонапты, или «натягиватели верёвок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
История теоремы Пифагора
4
3
5
Слайд 5Ван-дер-Варден (голландский математик) сделал вывод о большой вероятности того, что теорема
о квадрате гипотенузы была известна в Вавилоне уже около XVIII века до н. э.
Слайд 6«Принадлежит ли эта формула лично перу Пифагора…, но мы можем уверенно
считать, что она принадлежит древнейшему периоду пифагорейской математики».
Сегодня существует около 367 разнообразных доказательств этой теоремы.
Сегодня существует около 367 разнообразных доказательств этой теоремы.
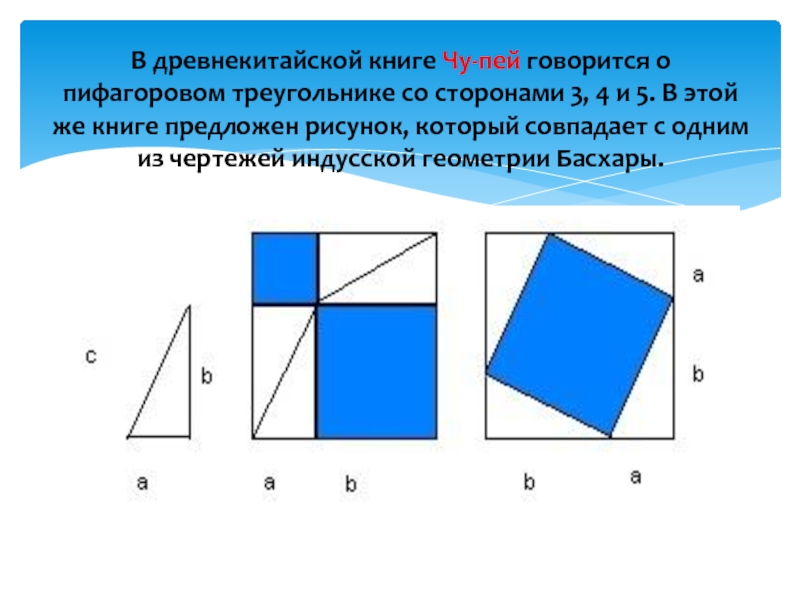
Слайд 7В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3,
4 и 5. В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.
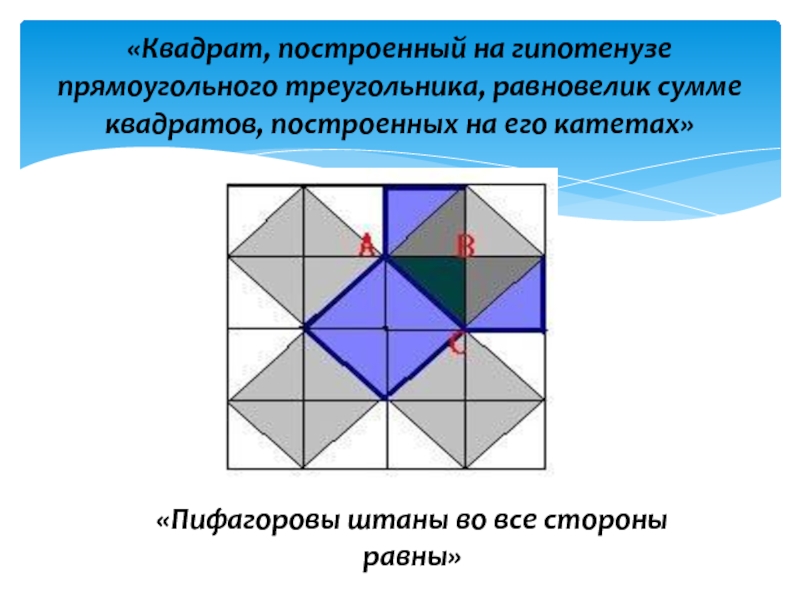
Слайд 8«Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на
его катетах»
«Пифагоровы штаны во все стороны равны»
Слайд 10Это любопытное древнекитайское доказательство получило название «Стул невесты» - из-за похожей
на стул фигуры, которая получается в результате всех построений:
Слайд 12Примеры Пифагоровых троек:
(3, 4, 5), (6, 8, 10), (5, 12,
13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 35, 45), (14, 48, 50), (30, 40, 50) и т.д