- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 8 класс на тему: Теорема Фалеса. Пропорциональные отрезки
Содержание
- 1. Презентация по геометрии 8 класс на тему: Теорема Фалеса. Пропорциональные отрезки
- 2. Задачи на готовых чертежахНайти углы трапеции75°40°АВСDЕНайти углы трапецииBЕ║CD60°60°5ААВАСВАDСВАКРAD=7.Найти: СD
- 3. Найти углы трапецииААВАСВАххх2х2х +х+90° = 180°3х =
- 4. Ответы к задачам1. ∠A = ∠D =
- 5. Великий учёный Фалес Милетский основал одну из
- 6. Теорема: если параллельные прямые, пересекающие стороны угла,
- 7. Задачи на готовых чертежахABCEF4512EF║AC. Найти:РАВСAA1A2A3A4B1B2B3B4АВ4=40. Найти:В2В3.АМВСNDOДоказать:АО = СОАВСDМКЕ10МК║ВЕ║СD, AD=16.Найти:АК.
- 8. ЕММ1М2М3М4МК II М1К1 II М2К2 II М3К3
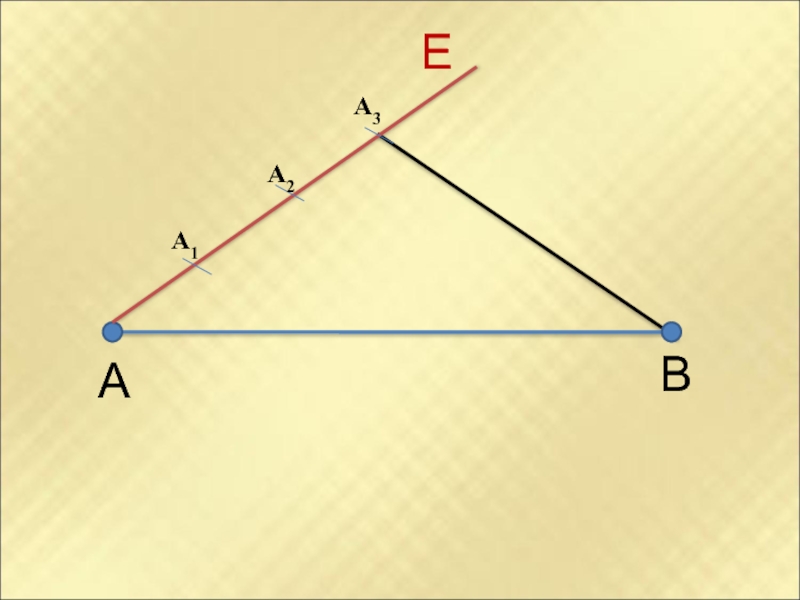
- 9. Разделите отрезок на три равные части
- 10. АВЕA1A2A3
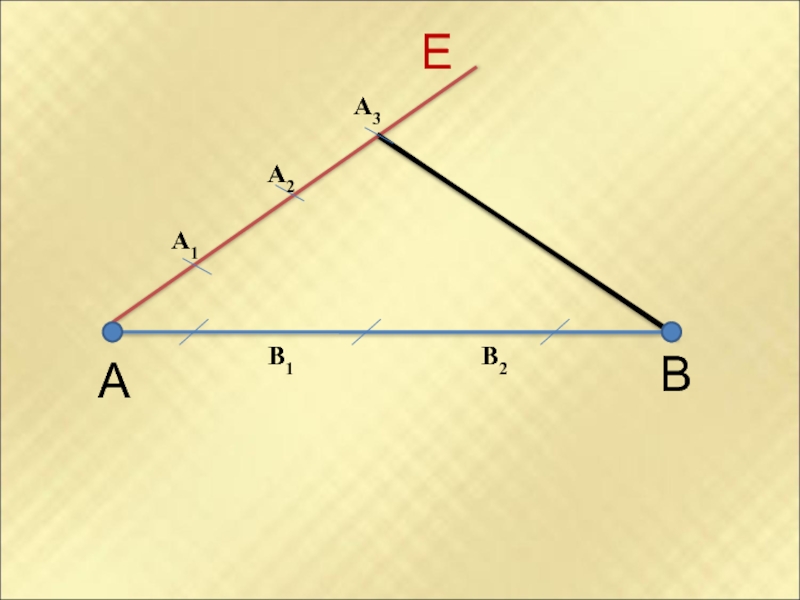
- 11. АВЕA1A2A3B1B2
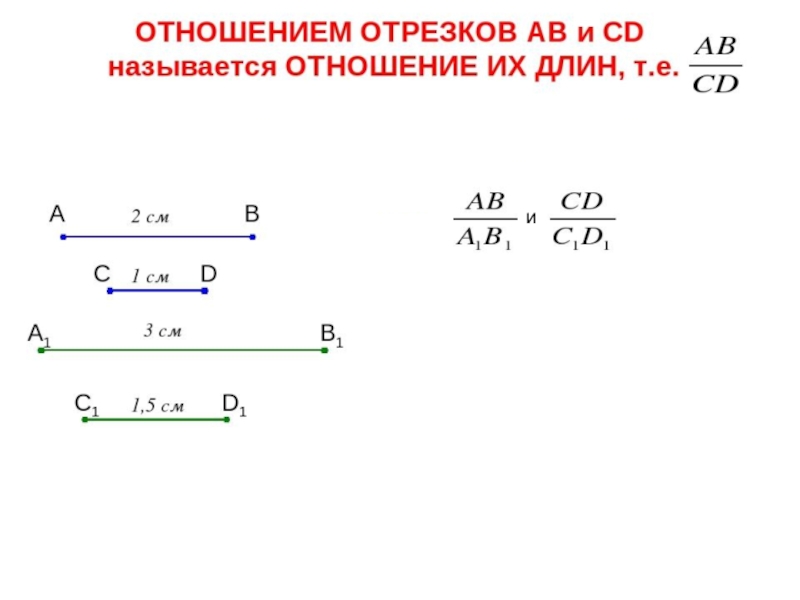
- 12. и
- 13. Если параллельные прямые, пересекают стороны угла, то
- 14. Свойство медиан треугольника
- 15. ИсследованиеПостройте произвольный треугольник;Проведите две медианы из любых
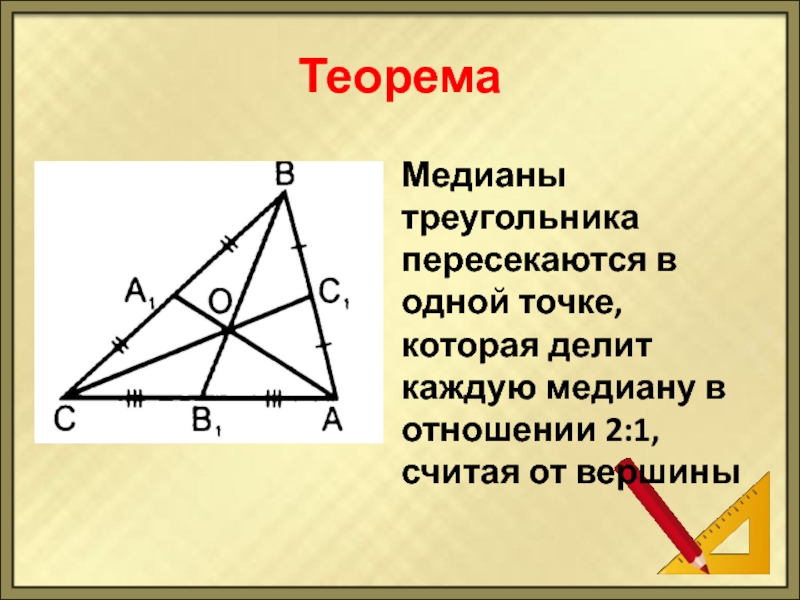
- 16. ТеоремаМедианы треугольника пересекаются в одной точке, которая
- 17. Дано: ΔABC, АА1, ВВ1, СС1 – медианыАА1∩
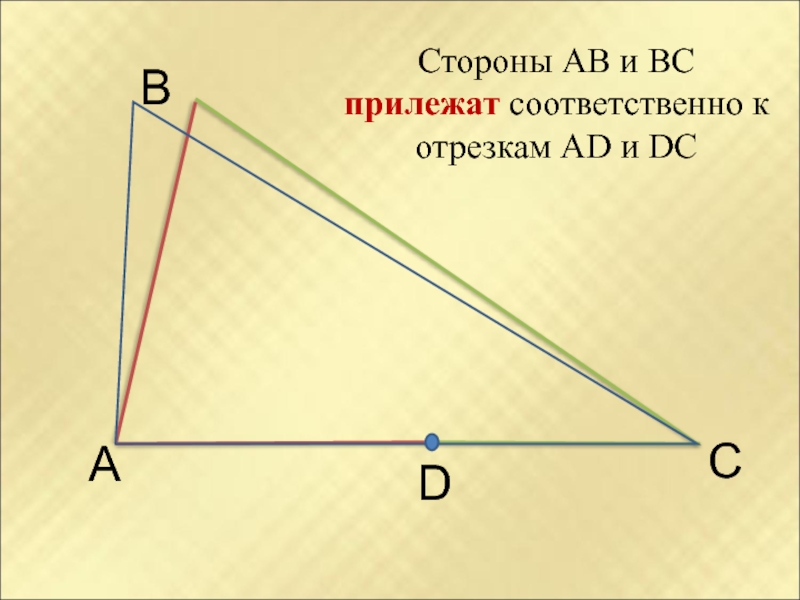
- 18. АВСDСтороны АВ и ВС прилежат соответственно к отрезкам АD и DC
- 19. Свойство биссектрисы треугольникаБиссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим к ним сторонам.АВСD
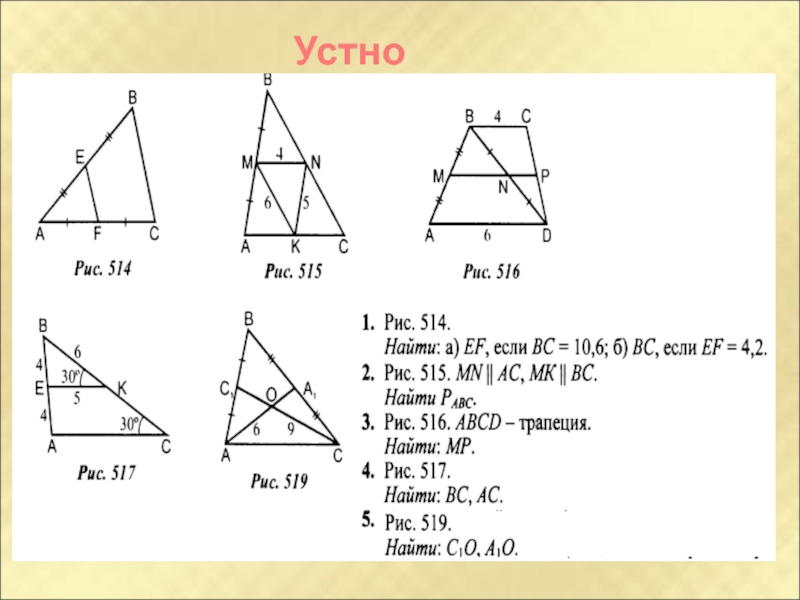
- 20. Устно
Слайд 2
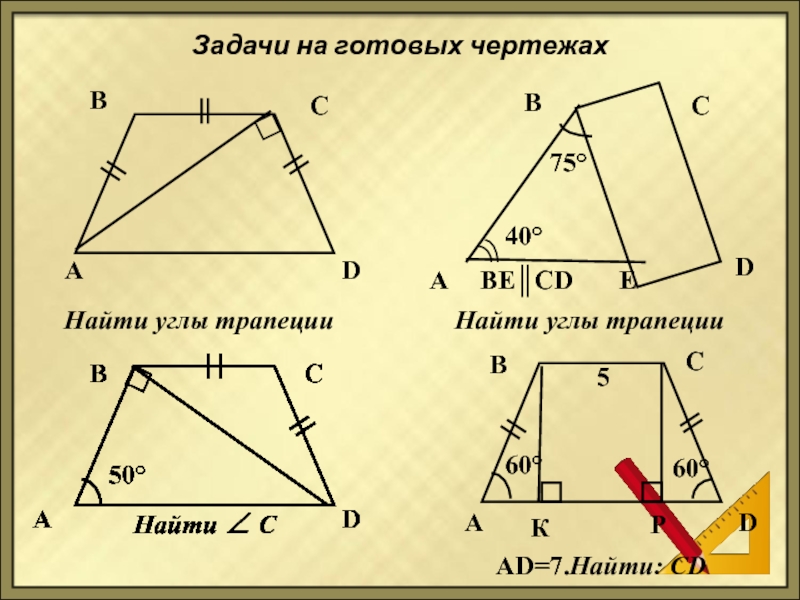
Задачи на готовых чертежах
Найти углы трапеции
75°
40°
А
В
С
D
Е
Найти углы трапеции
BЕ║CD
60°
60°
5
А
А
В
А
С
В
А
D
С
В
А
К
Р
AD=7.Найти: СD
Слайд 3
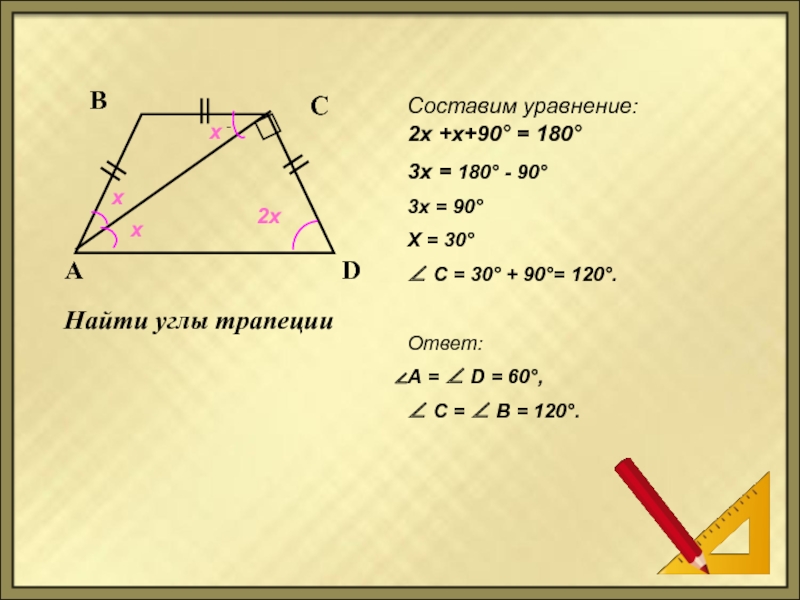
Найти углы трапеции
А
А
В
А
С
В
А
х
х
х
2х
2х +х+90° = 180°
3х = 180° - 90°
3х =
Х = 30°
∠ C = 30° + 90°= 120°.
Ответ:
А = ∠ D = 60°,
∠ C = ∠ B = 120°.
Составим уравнение:
Слайд 4Ответы к задачам
1. ∠A = ∠D = 60°, ∠B = ∠C
2. ∠A=40°, ∠D=65°, ∠C=115°, ∠B=140°.
3. ∠C = 100°.
4. CM =2.
Слайд 5Великий учёный Фалес Милетский основал одну из прекраснейших наук- геометрию. Известно,
624-547г.г. до н.э.
Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.
Фалес- математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны. Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой
Фалес Милетский
Слайд 6
Теорема: если параллельные прямые, пересекающие стороны угла, отсекают на одной его
А1
А3
Дано: угол, параллельные прямые пересекают стороны угла, А1А2=А2А3
Доказать: В1В2=В2В3
Доказательство.
Проведём через точку В2 прямую ЕF, параллельную прямой А1А3.
По свойству параллелограмма А1А2=FВ2, А2А3=В2Е.
Так как А1А2=А2А3, то FВ2=В2Е
Треугольники В2В1F и В2В3Е равны по второму признаку ( у них В2F=В2Е по доказанному. Углы при вершине В2 равны как вертикальные, а углы В2FВ3равны как внутренние накрест лежащие при параллельных А1В1 и А3В3 и секущей ЕF.)
Из равенства треугольников следует равенство сторон: В1В2=В2В3
А2
В1
В2
В3
F
E
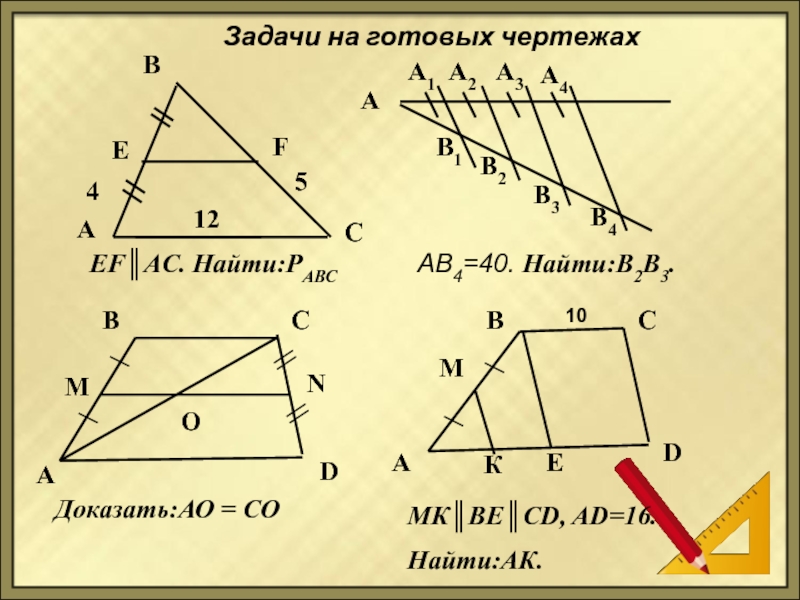
Слайд 7Задачи на готовых чертежах
A
B
C
E
F
4
5
12
EF║AC. Найти:РАВС
A
A1
A2
A3
A4
B1
B2
B3
B4
АВ4=40. Найти:В2В3.
А
М
В
С
N
D
O
Доказать:АО = СО
А
В
С
D
М
К
Е
10
МК║ВЕ║СD, AD=16.
Найти:АК.
Слайд 8
Е
М
М1
М2
М3
М4
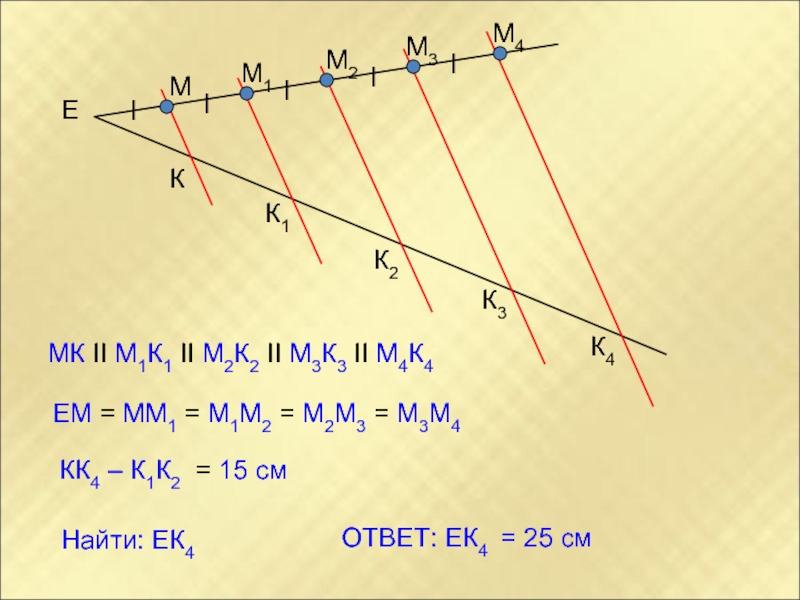
МК II М1К1 II М2К2 II М3К3 II М4К4
ЕМ = ММ1
ОТВЕТ: ЕК4 = 25 см
КК4 – К1К2 = 15 см
Найти: ЕК4
Слайд 13Если параллельные прямые, пересекают стороны угла, то отрезки, образовавшиеся на одной
Слайд 15Исследование
Постройте произвольный треугольник;
Проведите две медианы из любых двух вершин треугольника.
Точку пересечения
Возьмите линейку и измерьте расстояние от вершины треугольника до точки О. Запишите ответ………..
От точки О до середины противоположной стороны (точка образованная данной медианой). Запишите ответ………………
Во сколько раз расстояние от вершины треугольника до точки О больше расстояния от точки О до середины противоположной стороны? Ответ:………………………………
Запишите результат в виде отношения………………….
Сформулируйте вывод: Медианы треугольника пересекаются в ………. точке, которая делит каждую медиану в отношении………., считая от вершины.
Слайд 16Теорема
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в
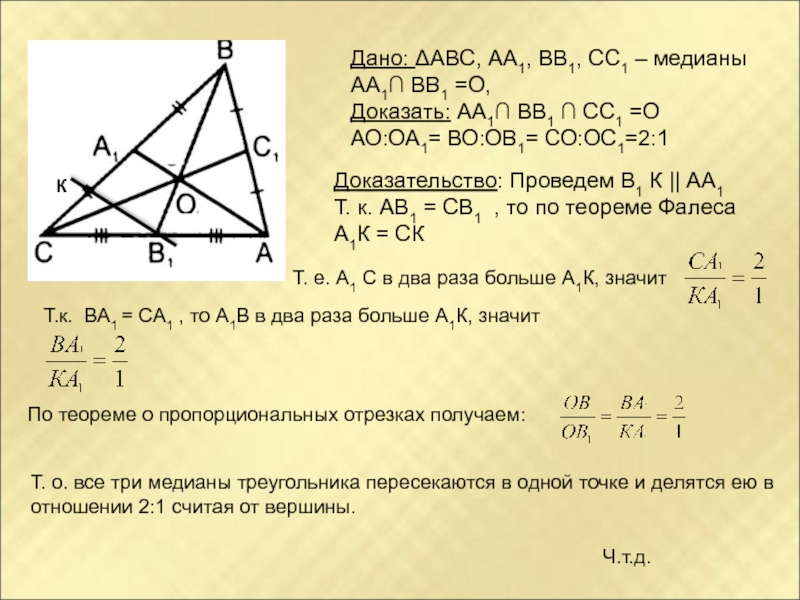
Слайд 17Дано: ΔABC, АА1, ВВ1, СС1 – медианы
АА1∩ ВВ1 =О,
Доказать: АА1∩ ВВ1
АО:ОА1= ВО:ОВ1= СО:ОС1=2:1
Доказательство: Проведем В1 К || АА1
Т. к. АВ1 = СВ1 , то по теореме Фалеса
А1К = СК
К
Т. е. А1 С в два раза больше А1К, значит
Т. о. все три медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1 считая от вершины.
Ч.т.д.
Т.к. ВА1 = СА1 , то А1В в два раза больше А1К, значит
По теореме о пропорциональных отрезках получаем:
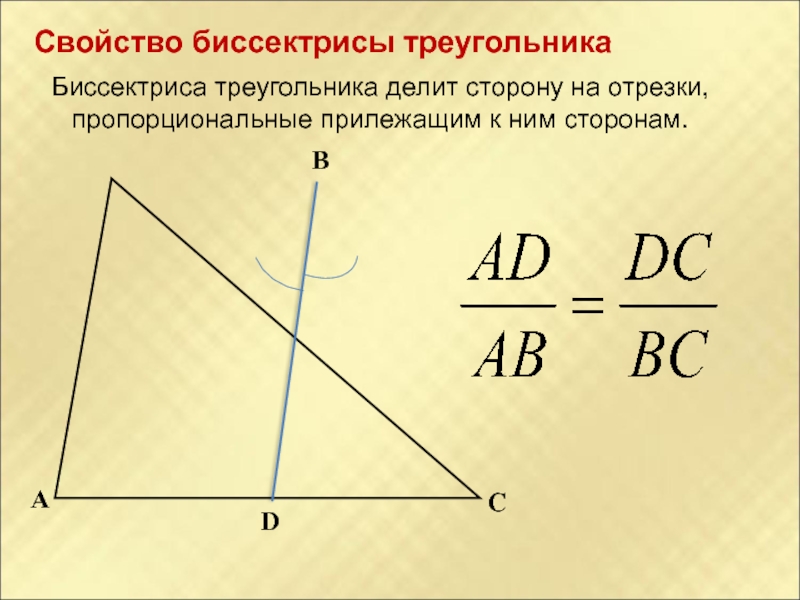
Слайд 19Свойство биссектрисы треугольника
Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим к
А
В
С
D