- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 8 класс на тему: Признаки подобия треугольников.
Содержание
- 1. Презентация по геометрии 8 класс на тему: Признаки подобия треугольников.
- 2. Содержание:Пропорциональные отрезки.Определение подобных треугольников.Отношение площадей подобных треугольников.Первый признак подобия треугольников.Второй признак подобия треугольников.Третий признак подобия треугольников.
- 3. Пропорциональные отрезки.Отношением отрезков АВ и CD называется
- 4. Определение подобных треугольников.Пусть у двух треугольников АВС
- 5. Отношение площадей подобных треугольников.Теорема: Отношение площадей двух
- 6. Первый признак подобия треугольников.Теорема: Если два угла
- 7. Второй признак подобия треугольников.Теорема: Если две стороны
- 8. Третий признак подобия треугольников.Теорема: Если три стороны
Слайд 1«Подобие треугольников.
Признаки подобия треугольников»
Пономарева Юлия Васильевна,
учитель математики
МБОУ Каменно-Балковская СОШ
Слайд 2Содержание:
Пропорциональные отрезки.
Определение подобных треугольников.
Отношение площадей подобных треугольников.
Первый признак подобия треугольников.
Второй признак
Третий признак подобия треугольников.
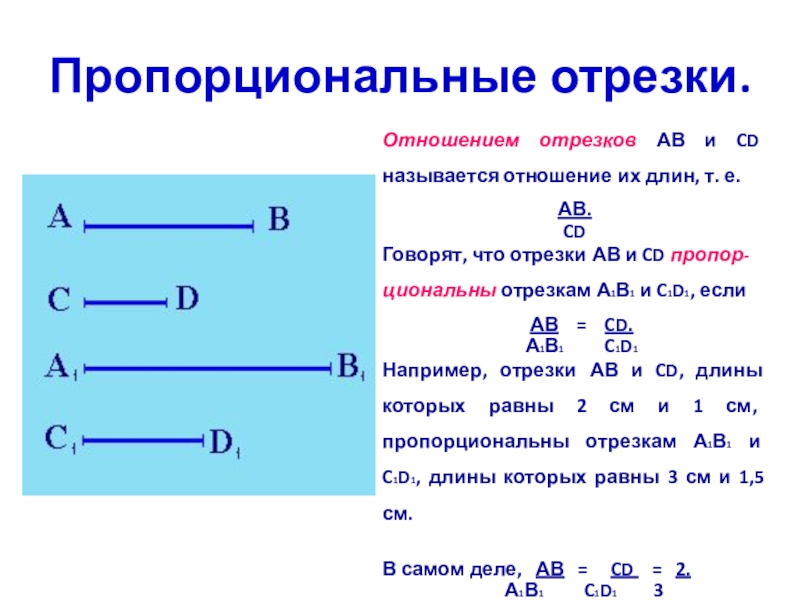
Слайд 3Пропорциональные отрезки.
Отношением отрезков АВ и CD называется отношение их длин, т.
АВ.
CD
Говорят, что отрезки АВ и CD пропор-циональны отрезкам А1В1 и C1D1, если
АВ = CD.
А1В1 C1D1
Например, отрезки АВ и CD, длины которых равны 2 см и 1 см, пропорциональны отрезкам А1В1 и C1D1, длины которых равны 3 см и 1,5 см.
В самом деле, АВ = CD = 2.
А1В1 C1D1 3
Слайд 4Определение подобных треугольников.
Пусть у двух треугольников АВС и А1В1С1 соответствующие углы
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
АВ ВС СА
А1В1 В1С1 С1А1
k
Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
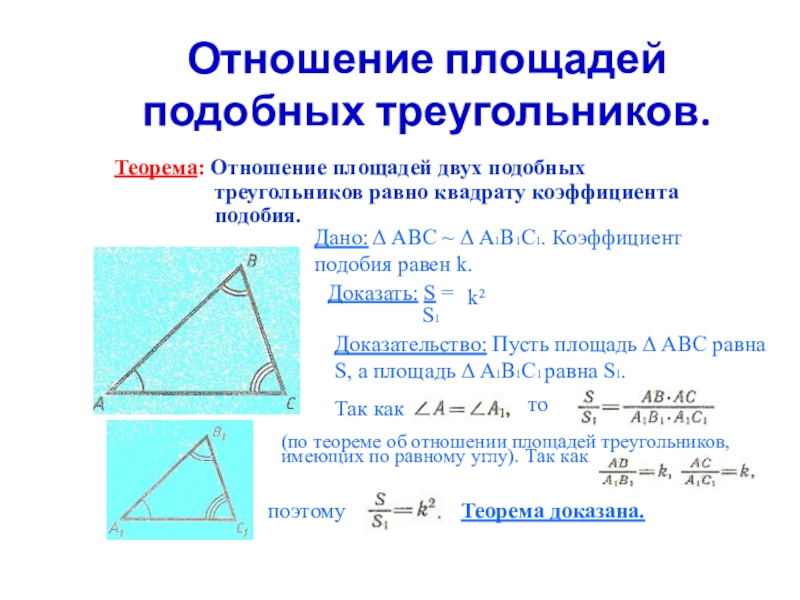
Слайд 5Отношение площадей подобных треугольников.
Теорема: Отношение площадей двух подобных
подобия.
Дано: АВС ~ А1В1С1. Коэффициент подобия равен k.
Доказать: S =
S1
k²
Доказательство: Пусть площадь АВС равна S, а площадь А1В1С1 равна S1.
Так как
то
(по теореме об отношении площадей треугольников, имеющих по равному углу). Так как
поэтому
Теорема доказана.
Слайд 6Первый признак подобия треугольников.
Теорема: Если два угла одного треугольника соответственно
Дано: АВС, А1В1С1.
Доказать: АВС ~ А1В1С1.
Доказательство: по теореме о сумме углов треугольника
и, значит,
Таким образом, углы АВС
соответственно равны углам А1В1С1. Докажем, что стороны АВС пропорциональны сходственным сторонам А1В1С1.
Т.к.
то
Из этих равенств следует, что
Аналогично, используя равенства
получаем
Итак, стороны АВС пропорциональны сходственным сторонам А1В1С1. Теорема доказана.
Слайд 7Второй признак подобия треугольников.
Теорема: Если две стороны одного треугольника пропорциональны двум
Дано: АВС, А1В1С1,, у которых
Доказать: АВС ~ А1В1С1.
Доказательство: Достаточно доказать, что
Рассмотрим АВС2, у которого
Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия треугольников, поэтому
С другой стороны, по условию
Из этих двух равенств получаем АС = АС2.
АВС и АВС2 равны по двум сторонам и углу между ними (АВ – общая сторона, АС=АС2 и )
Отсюда следует, что
а так, как
Теорема доказана.
Слайд 8Третий признак подобия треугольников.
Теорема: Если три стороны одного треугольника пропорциональны трем
Дано: АВС, А1В1С1,, у которых
Доказать: АВС ~ А1В1С1.
Доказательство: Достаточно доказать, что
Рассмотрим АВС2, у которого
Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия треугольников, поэтому
Сравнивая эти равенства с равенствами, которые записаны в дано, получаем:
АВС= АВС2 по трем сторонам. Отсюда следует, что
Теорема доказана.
а так как