Магомедзагировна
МКОУ СОШ №11
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 7 класс
Содержание
- 1. Презентация по геометрии 7 класс
- 2. Д/зп.17; № 105.Вопросы 1- 5; 7 -
- 3. Проверка Д/з
- 4. Устно: Перпендикуляр к прямой. №100 –
- 5. №100 Начертите прямую а и отметьте точки
- 6. Тест. Вопрос 1.АРDКЕСДля доказательства равенства треугольников АРК
- 7. Тест. Вопрос 2.АВFКМNИз равенства треугольников АВК и
- 8. Тест. Вопрос 3.АВС1СА1В1Треугольники АВС и А1В1С1 равны,
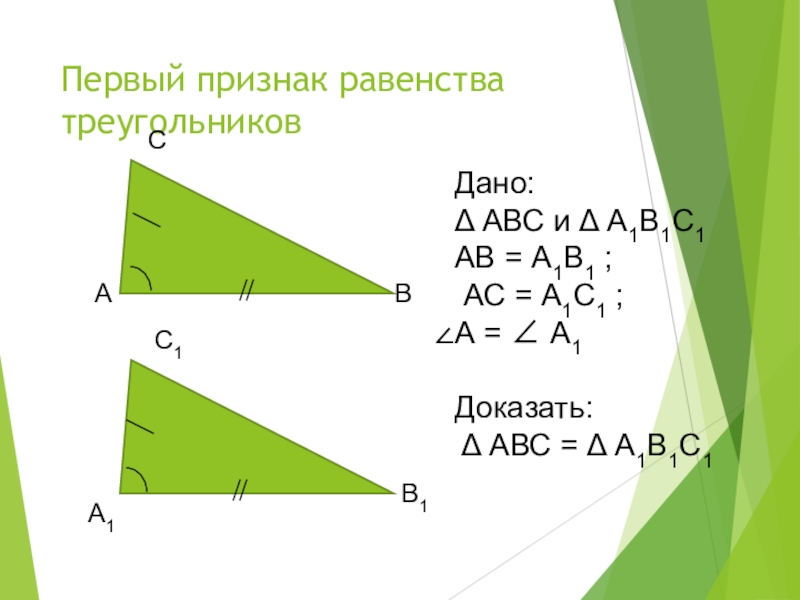
- 9. Первый признак равенства треугольниковАВСВ1С1А1Дано: Δ АВС и
- 10. Медианы, биссектрисыи высоты треугольникаИзучение нового материала
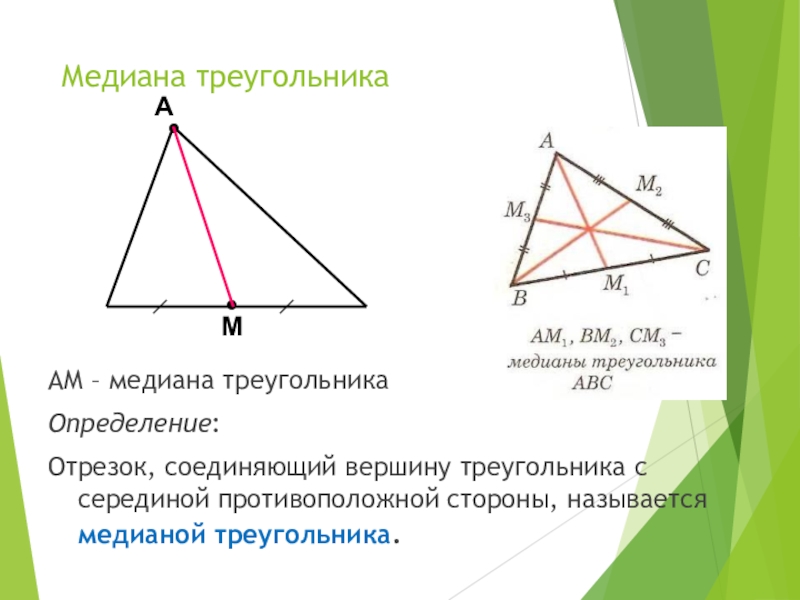
- 11. Медиана треугольникаАМ – медиана треугольникаОпределение:Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника...АМ
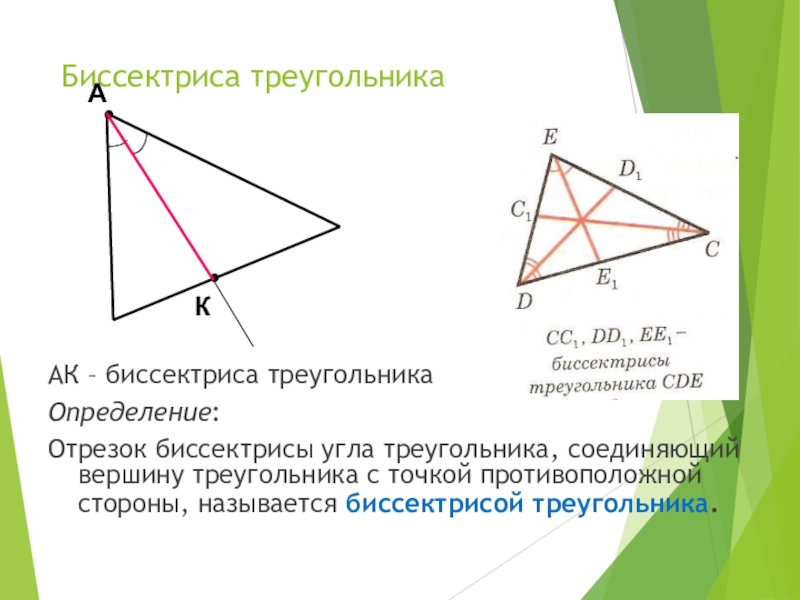
- 12. Биссектриса треугольникаАК – биссектриса треугольникаОпределение:Отрезок биссектрисы угла
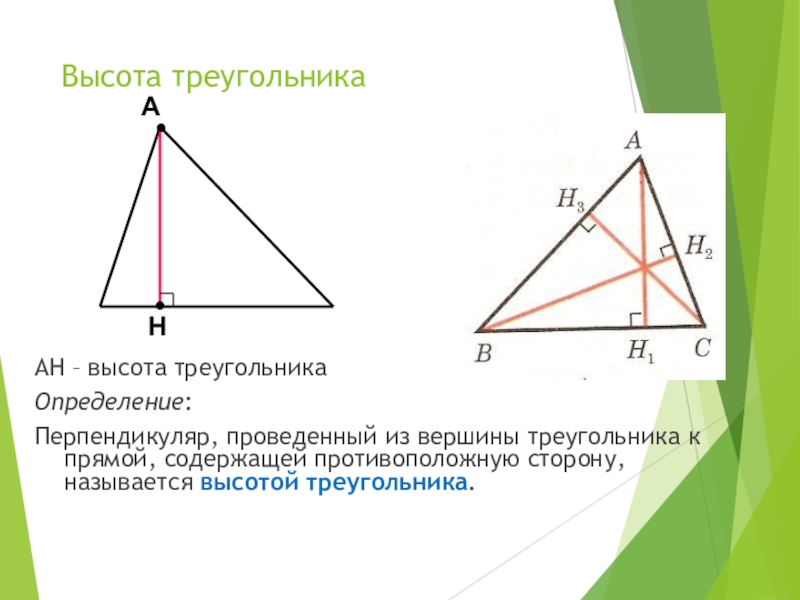
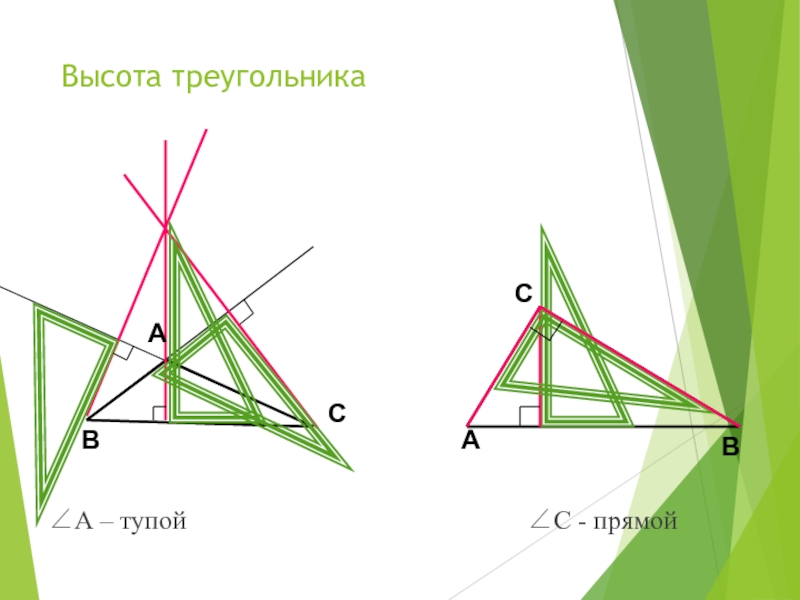
- 13. Высота треугольникаАН – высота треугольникаОпределение:Перпендикуляр, проведенный из
- 14. Высота треугольника∠А – тупой
- 15. Решение задач
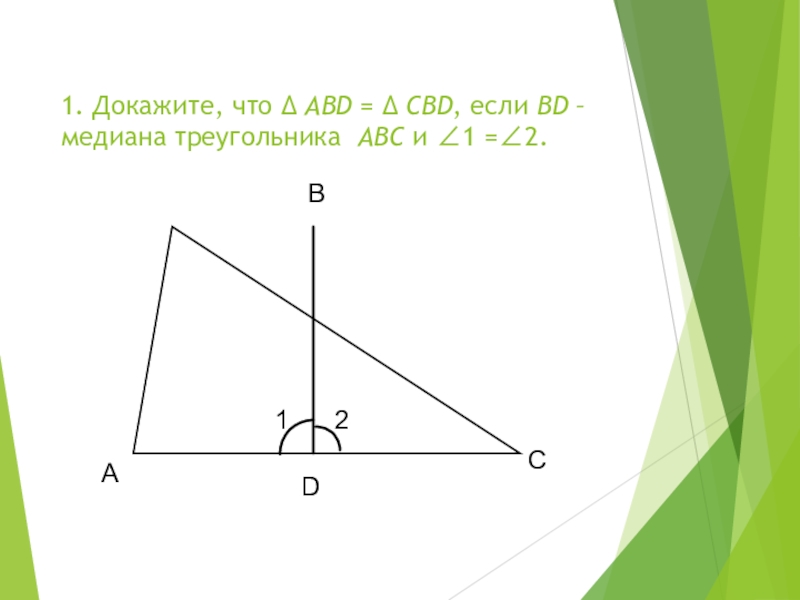
- 16. 1. Докажите, что Δ АВD =
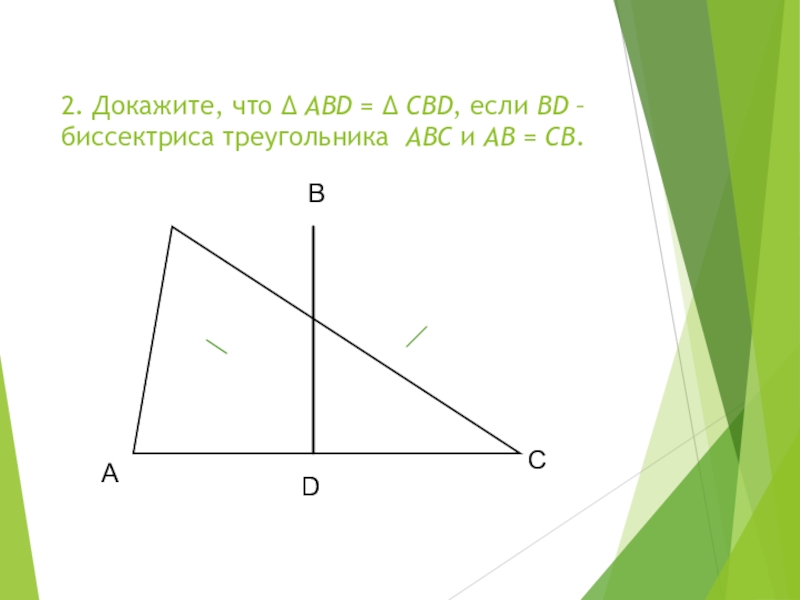
- 17. 2. Докажите, что Δ АВD =
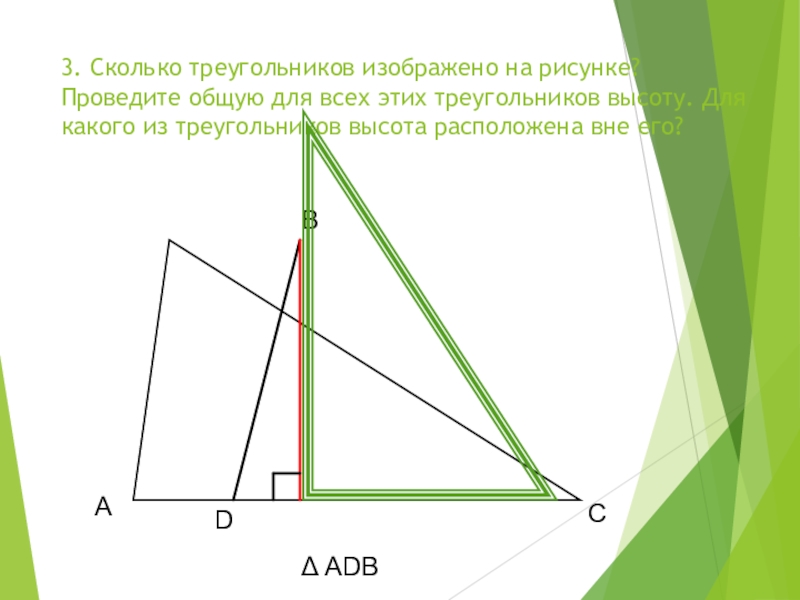
- 18. 3. Сколько треугольников изображено на рисунке?
- 19. № 97 (д/з) Отрезки АС и
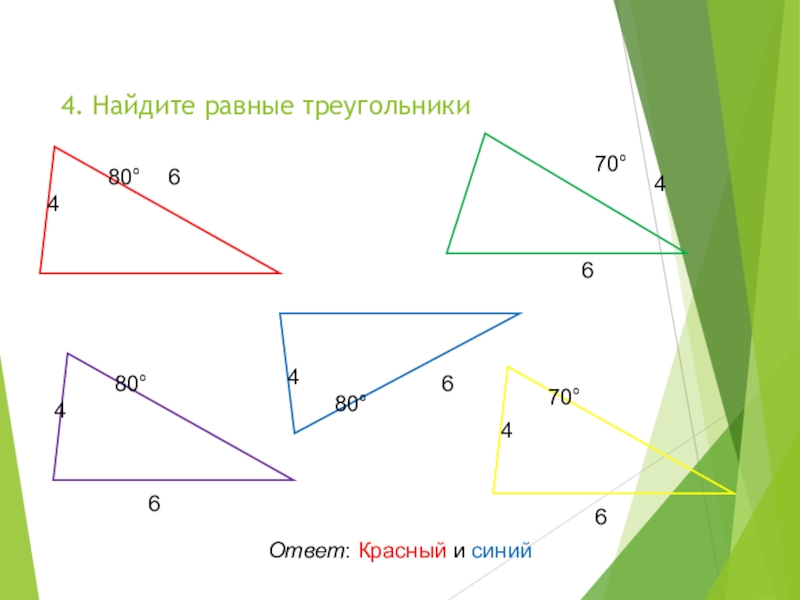
- 20. 4. Найдите равные треугольники66444680°70°80°80°70°4664Ответ: Красный и синий
- 21. №101 Начертите треугольник. С помощью масштабной
Д/зп.17; № 105.Вопросы 1- 5; 7 - 9 (стр. 50)План урокаПроверка д/зИзучение нового материалаРешение задач на равенство треугольников (№97 и др.)
Слайд 1Урок геометрии 7 класс
на тему:
«Медианы, биссектрисы и высоты треугольника»
Учитель математики
Ильясова Заира
Слайд 2Д/з
п.17; № 105.
Вопросы 1- 5; 7 - 9 (стр. 50)
План урока
Проверка
д/з
Изучение нового материала
Решение задач на равенство треугольников (№97 и др.)
Изучение нового материала
Решение задач на равенство треугольников (№97 и др.)
Слайд 4Устно: Перпендикуляр к прямой.
№100 – показать на доске
Рассмотрим прямую а
и точку А, не лежащую на этой прямой. Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если
прямые АН и а перпендикулярны. Точка Н называется
основанием перпендикуляра.
прямые АН и а перпендикулярны. Точка Н называется
основанием перпендикуляра.
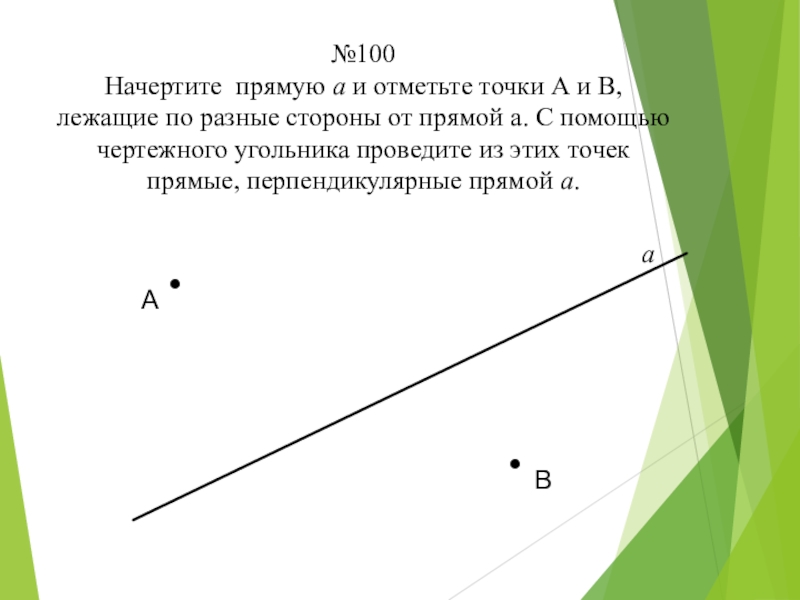
Слайд 5№100 Начертите прямую а и отметьте точки А и В, лежащие по
разные стороны от прямой а. С помощью чертежного угольника проведите из этих точек прямые, перпендикулярные прямой а.
.
.
А
В
а
Слайд 6Тест. Вопрос 1.
А
Р
D
К
Е
С
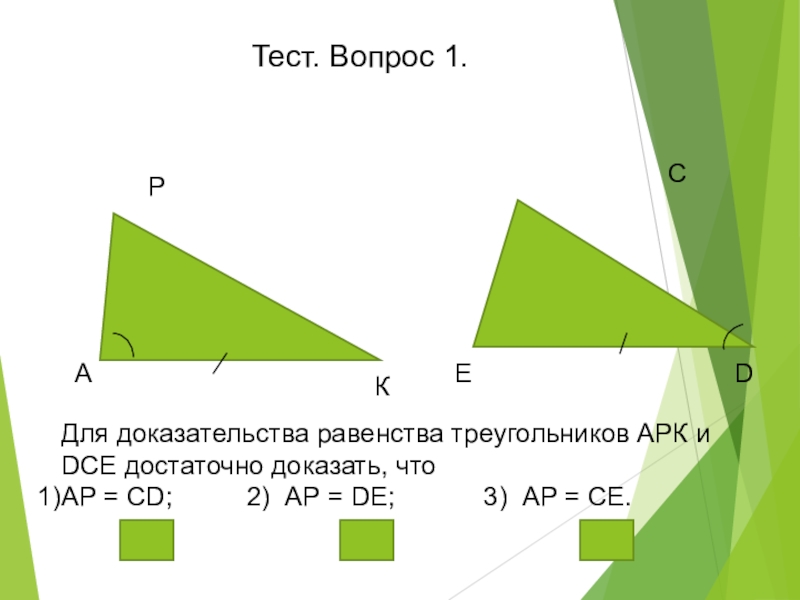
Для доказательства равенства треугольников АРК и DСЕ достаточно доказать,
что
АР = СD; 2) АР = DЕ; 3) АР = СЕ.
АР = СD; 2) АР = DЕ; 3) АР = СЕ.
Слайд 7Тест. Вопрос 2.
А
В
F
К
М
N
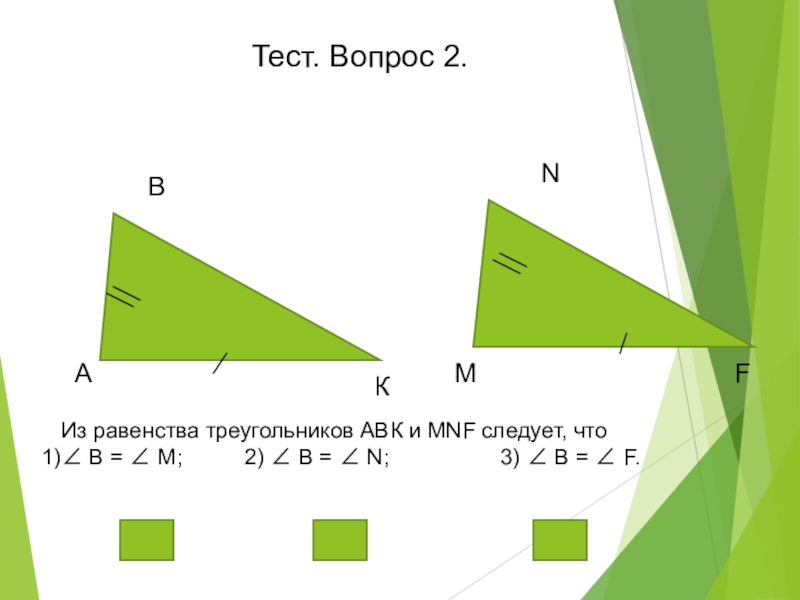
Из равенства треугольников АВК и MNF следует, что
∠
В = ∠ М; 2) ∠ В = ∠ N; 3) ∠ B = ∠ F.
Слайд 8Тест. Вопрос 3.
А
В
С1
С
А1
В1
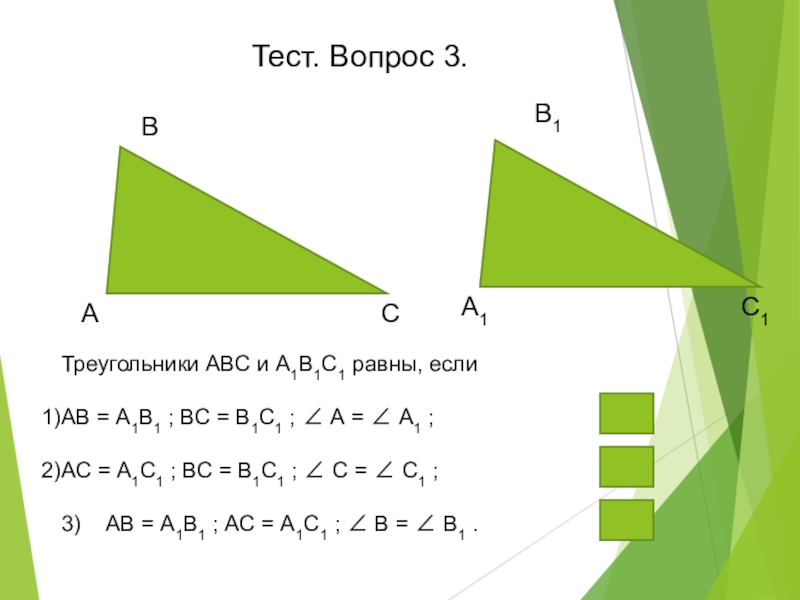
Треугольники АВС и А1В1С1 равны, если
АВ = А1В1
; ВС = В1С1 ; ∠ А = ∠ А1 ;
АС = А1С1 ; ВС = В1С1 ; ∠ С = ∠ С1 ;
3) АВ = А1В1 ; АС = А1С1 ; ∠ В = ∠ В1 .
АС = А1С1 ; ВС = В1С1 ; ∠ С = ∠ С1 ;
3) АВ = А1В1 ; АС = А1С1 ; ∠ В = ∠ В1 .
Слайд 9Первый признак равенства треугольников
А
В
С
В1
С1
А1
Дано:
Δ АВС и Δ А1В1С1
АВ =
А1В1 ;
АС = А1С1 ;
А = ∠ А1
Доказать:
Δ АВС = Δ А1В1С1
АС = А1С1 ;
А = ∠ А1
Доказать:
Δ АВС = Δ А1В1С1
Слайд 11Медиана треугольника
АМ – медиана треугольника
Определение:
Отрезок, соединяющий вершину треугольника с серединой противоположной
стороны, называется медианой треугольника.
.
.
А
М
Слайд 12Биссектриса треугольника
АК – биссектриса треугольника
Определение:
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника
с точкой противоположной стороны, называется биссектрисой треугольника.
.
.
А
К
Слайд 13Высота треугольника
АН – высота треугольника
Определение:
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой треугольника.
.
.
А
Н
Слайд 18 3. Сколько треугольников изображено на рисунке? Проведите общую для всех этих
треугольников высоту. Для какого из треугольников высота расположена вне его?
D
В
А
С
Δ ADB
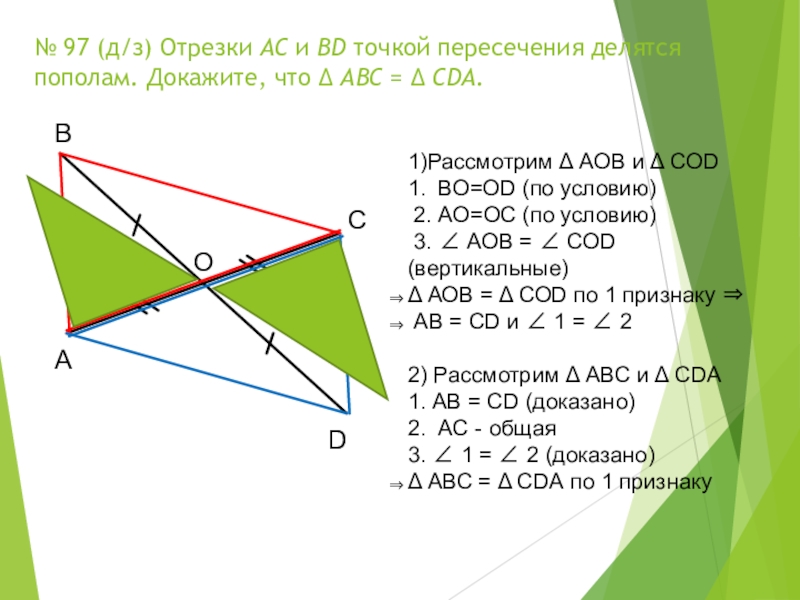
Слайд 19 № 97 (д/з) Отрезки АС и ВD точкой пересечения делятся пополам.
Докажите, что Δ АВС = Δ СDА.
В
D
С
А
О
1)Рассмотрим Δ АОВ и Δ СОD
1. ВО=ОD (по условию)
2. АО=ОС (по условию)
3. ∠ АОВ = ∠ СОD (вертикальные)
Δ АОВ = Δ СОD по 1 признаку ⇒
АВ = СD и ∠ 1 = ∠ 2
2) Рассмотрим Δ АВС и Δ СDА
1. АВ = СD (доказано)
2. АС - общая
3. ∠ 1 = ∠ 2 (доказано)
Δ АВС = Δ СDА по 1 признаку
Слайд 21 №101 Начертите треугольник. С помощью масштабной линейки отметьте середины сторон и проведите
медианы треугольника.
№102
Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.
№103
Начертите треугольник АВС с тремя острыми углами и треугольник МNP, у которого угол М тупой. С помощью чертежного угольника проведите высоты каждого треугольника.
