- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 7 кл
Содержание
- 1. Презентация по геометрии 7 кл
- 2. Повторение Вставьте недостающие слова:Две прямые на плоскости
- 3. Повторение Назовите пары накрест лежащих, соответственных и односторонних углов.12345678
- 4. Тема урокаАКСИОМЫ ПАРАЛЛЕЛЬНОСТИ ЕВКЛИДА. НАЧАЛА ЕВКЛИДА.Л.ЭЙЛЕР, Н.И. ЛОБАЧЕВСКИЙ. ИСТОРИЯ ПЯТОГО ПОСТУЛАТА.
- 5. Об аксиомах геометрии Само слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».
- 6. Сначала формулируются исходные положения - аксиомыНа их
- 7. Аксиомы первой главы1. Через любые две точки
- 8. Аксиома параллельных прямых Рассмотрим произвольную прямую а
- 9. Аксиома параллельных прямыхИтак, через точку М проходит
- 10. Аксиома параллельных прямыхОказывается этот вопрос имеет большую
- 11. Аксиома параллельных прямыхИ лишь в прошлом веке
- 12. Об аксиомах геометрии Познакомимся с одной из самых известных аксиом геометрии
- 13. Аксиома параллельных прямыхЧерез точку,
- 14. Слайд 14
- 15. 1. Если прямая пересекает одну
Слайд 2Повторение
Вставьте недостающие слова:
Две прямые на плоскости называются параллельными, если
Если при пересечении двух прямых секущей __________________________________, то прямые параллельны.
Если при пересечении двух прямых секущей __________________________________, то прямые параллельны.
Если при пересечении двух прямых секущей __________________________________, то прямые параллельны.
они не пересекаются
накрест лежащие углы равны
сумма односторонних углов равна 1800
соответственные углы равны
Слайд 4Тема урока
АКСИОМЫ ПАРАЛЛЕЛЬНОСТИ ЕВКЛИДА. НАЧАЛА ЕВКЛИДА.
Л.ЭЙЛЕР, Н.И. ЛОБАЧЕВСКИЙ.
ИСТОРИЯ ПЯТОГО ПОСТУЛАТА.
Слайд 5Об аксиомах геометрии
Само слово «аксиома» происходит от греческого «аксиос», что
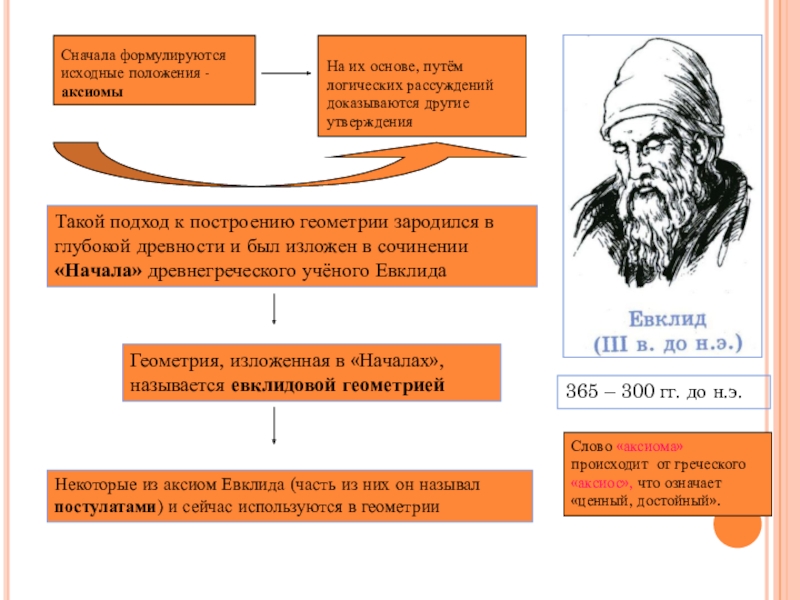
Слайд 6Сначала формулируются исходные положения - аксиомы
На их основе, путём логических рассуждений
Такой подход к построению геометрии зародился в глубокой древности и был изложен в сочинении «Начала» древнегреческого учёного Евклида
365 – 300 гг. до н.э.
Геометрия, изложенная в «Началах», называется евклидовой геометрией
Некоторые из аксиом Евклида (часть из них он называл постулатами) и сейчас используются в геометрии
Слово «аксиома» происходит от греческого «аксиос», что означает «ценный, достойный».
Слайд 7Аксиомы первой главы
1. Через любые две точки проходит прямая, и притом
2. На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
Слайд 8Аксиома параллельных прямых
Рассмотрим произвольную прямую а и точку М, не
а
М
Построение:
1. Проведем прямую с, проходящую через М и перпендикулярную а.
2. Проведем прямую b, проходящую через М и перпендикулярную с.
3. а ׀׀b на основании теоремы о двух прямых перпендикулярной третьей.
с
b
Слайд 9Аксиома параллельных прямых
Итак, через точку М проходит прямая b, параллельная прямой
Нам представляется, что если прямую b «повернуть» даже на очень малый угол вокруг точки М, то она пересечет прямую а (прямая b' на рисунке).
Иными словами, нам кажется, что через точку М нельзя провести другую прямую (отличную от b), параллельную прямой а.
А можно ли это утверждение доказать?
а
М
с
b
b’
Слайд 10Аксиома параллельных прямых
Оказывается этот вопрос имеет большую историю. В «Началах» Евклида
Слайд 11Аксиома параллельных прямых
И лишь в прошлом веке было окончательно выяснено, что
Огромную роль в решении этого вопроса сыграл великий русский математик Николай Иванович Лобачевский (1792—1856).
Слайд 13 Аксиома параллельных прямых
Через точку, не лежащую на данной
Слайд 14 Следствия из аксиомы
Утверждения,
Слайд 15 1. Если прямая пересекает одну из двух параллельных прямых,
2.Если две прямые параллельны третьей прямой, то они параллельны.
Следствия из аксиомы параллельных прямых
а
в
М
с
Доказательство:
Предположим, что прямая с не пересекает прямую в, значит, с в.
Тогда через т.М проходят две прямые а и с параллельные прямой в.
3. Но это противоречит аксиоме параллельных прямых, значит, прямая с пересекает прямую в.
а
в
с
Доказательство:
Предположим, что прямая а и прямая в пересекаются.
2. Тогда через т.М проходят две прямые а и в параллельные прямой с
3 . Но это противоречит аксиоме параллельных прямых.
4. Значит прямые а и в параллельны.
Способ рассуждения,, который называется
методом доказательства от противного