- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 11 класс по теме Многогранники
Содержание
- 1. Презентация по геометрии 11 класс по теме Многогранники
- 2. Слайд 2
- 3. Многогранник
- 4. Элементы многогранникаМногоугольники, из которых состоитмногогранная поверхность,
- 5. 1. Двугранный уголэто
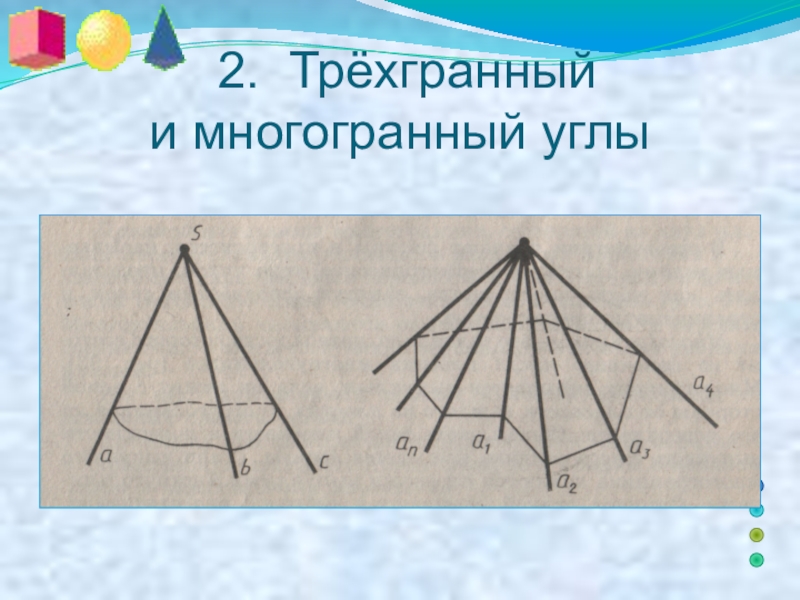
- 6. 2. Трёхгранный и многогранный углы
- 7. 3.ПризмаПризма – многогранник, состоящийиз двух плоских многоугольников,лежащих
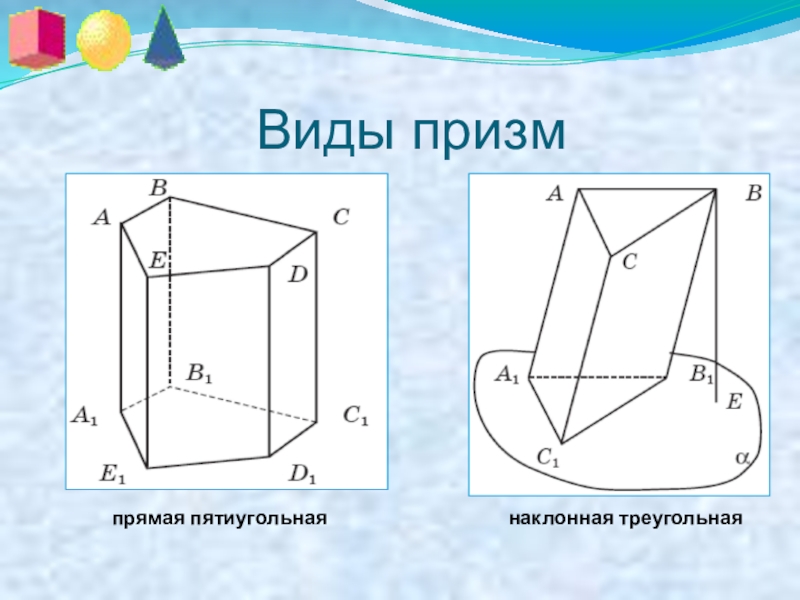
- 8. Виды призмнаклонная треугольная прямая пятиугольная
- 9. Площадь поверхности
- 10. 4.Параллелепипед Параллелепипед - это призма, в основании
- 11. Площадь и объём прямоугольного
- 12. 5. Пирамидаэто
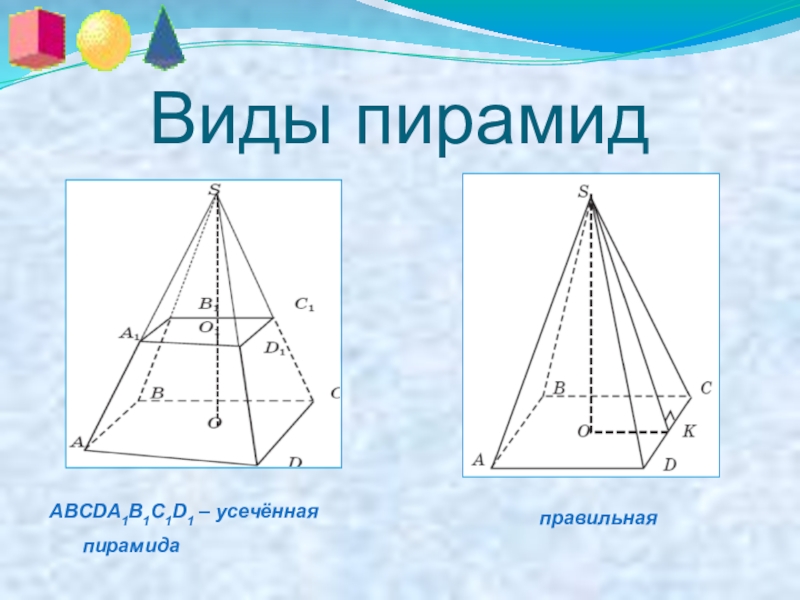
- 13. Виды пирамидABCDA1B1C1D1 – усечённая пирамида правильная
- 14. Нахождение объёма
- 15. 6.Правильные многогранникиВыпуклый многогранник называется правильным, если его
- 16. Вам понравилось?
Слайд 2
- определения основных фигур;
- их виды;
- изображение их на плоскости;
- и формулы для нахождения площади поверхности и объёма.
Выучив этот материал, Вы сможете решать задачи любой сложности.
Уважаемые ребята!
Удачи Вам!
Слайд 3
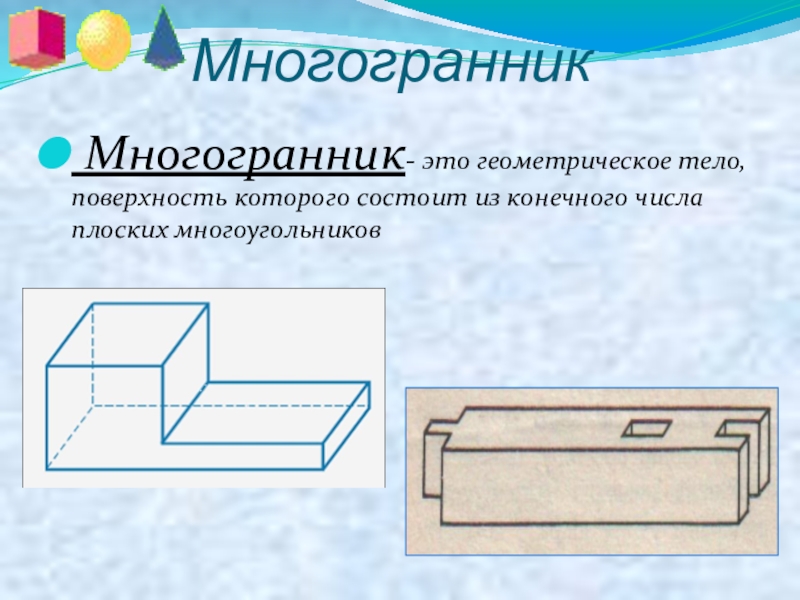
Многогранник
Многогранник- это геометрическое тело, поверхность
Слайд 4Элементы
многогранника
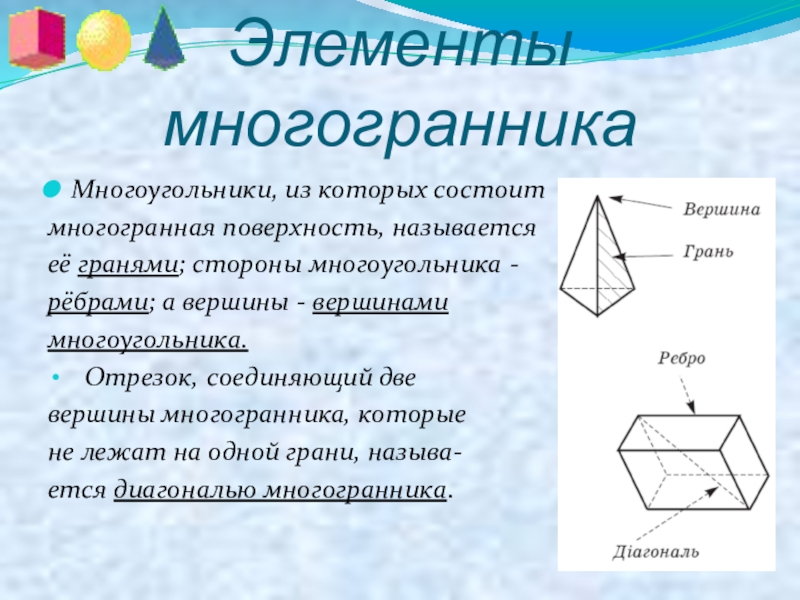
Многоугольники, из которых состоит
многогранная поверхность, называется
её гранями; стороны многоугольника -
рёбрами;
многоугольника.
Отрезок, соединяющий две
вершины многогранника, которые
не лежат на одной грани, называ-
ется диагональю многогранника.
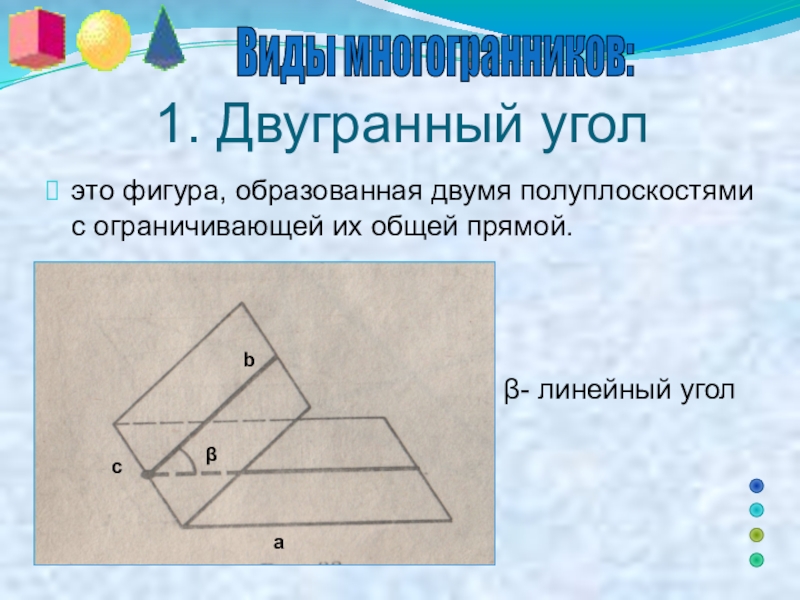
Слайд 5 1. Двугранный угол
это фигура, образованная двумя полуплоскостями
β- линейный угол
двугранного угла
а
b
c
c
β
a
c
b
β
Виды многогранников:
Слайд 73.Призма
Призма – многогранник, состоящий
из двух плоских многоугольников,
лежащих в различных плоскостях
и совмещаемых
переносом, и всех отрезков, соединя-
ющих соответствующие точки этих
многоугольников.
Слайд 9 Площадь поверхности
Боковая поверхность: S6 =p*l,
где р - периметр перпендикулярного сечения;
l- длина бокового ребра.
Полная поверхность: S = Sб + 2*S0
Объём: V= S*l,
где S- площадь перпендикулярного сечения;
l - длина бокового ребра.
Слайд 104.Параллелепипед
Параллелепипед - это призма, в основании которой лежит параллелограмм. Середина
параллелепипеда и есть центр его симметрии.
наклонный
а
прямоугольный
Слайд 11 Площадь и объём прямоугольного
Боковая поверхность:
Sб = 2*c*(a+b)
Полная поверхность:
S =2*(a*c+b*c+a*b)
Объём :
V= a*b*c
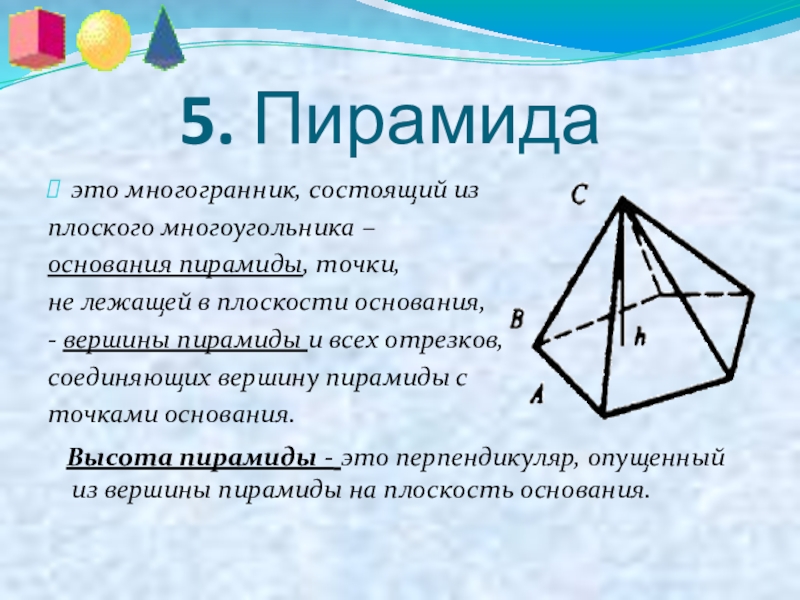
Слайд 12 5. Пирамида
это многогранник, состоящий из
плоского
основания пирамиды, точки,
не лежащей в плоскости основания,
- вершины пирамиды и всех отрезков,
соединяющих вершину пирамиды с
точками основания.
Высота пирамиды - это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Слайд 14 Нахождение объёма пирамид
Объём пирамиды:
V= ⅓*S0*h
Объём усечённой пирамиды:
S=⅓*h*(S1+√S1*S2+S2)
Полная поверхность пирамиды:
S=S1+S2+…+Sn
Слайд 156.Правильные многогранники
Выпуклый многогранник называется правильным, если его грани - правильные многоугольники
Тетраэдр Куб Октаэдр Додекаэдр Икосаэдр
Слайд 16Вам понравилось?
Ребята, надеюсь вы
Удачи!