- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии 10класс Изображение сечений тетраэдра и параллелепипеда
Содержание
- 1. Презентация по геометрии 10класс Изображение сечений тетраэдра и параллелепипеда
- 2. Секущая плоскостьЛюбая плоскость, по обе стороны от
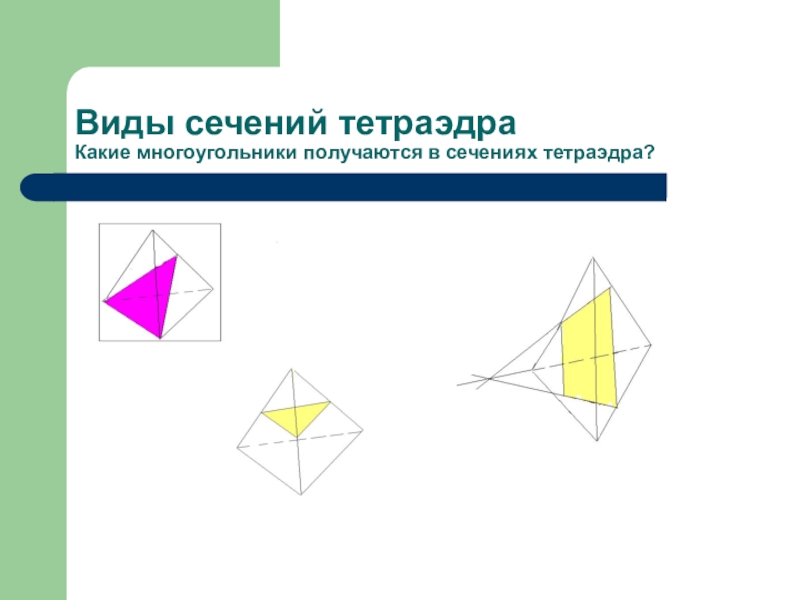
- 3. Виды сечений тетраэдра Какие многоугольники получаются в сечениях тетраэдра?
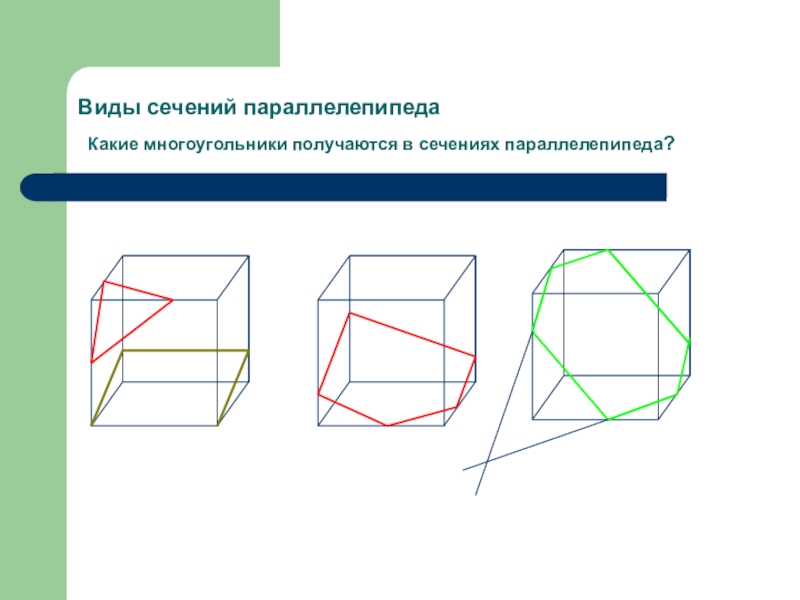
- 4. Виды сечений параллелепипеда Какие многоугольники получаются в сечениях параллелепипеда?
- 5. Рекомендации для построения сечений1 В каких
- 6. Ключевые задачиЗадача №1 Дан куб АВСДА1В1С1Д1. На
- 7. Ключевые задачиЗадача №2Дан куб АВСДА1В1С1Д1 и точка
- 8. Ключевые задачиЗадача №3Построить сечение куба АВСДА1В1С1Д1 плоскостью
- 9. Ключевые задачиЗадача №4Построить сечение куба плоскостью проходящей
- 10. Задания для группI (IV) группа1) Построить сечения
- 11. Задания для группIII (VI)группаПостроить сечение треугольной призмы
- 12. Контрольная работаКонтрольная работа (геом.- 10кл.) по теме
- 13. Контрольная работаВариант 3- уровень А-В1) Построить сечение
- 14. Спасибо за работуЖелаем успехов в учебе.
Секущая плоскостьЛюбая плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда), называется секущей плоскостью.Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.Многоугольник, сторонами которого являются эти отрезки, называют сечением тетраэдра (параллелепипеда).
Слайд 2Секущая плоскость
Любая плоскость, по обе стороны от которой имеются точки данного
тетраэдра (параллелепипеда), называется секущей плоскостью.
Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называют сечением тетраэдра (параллелепипеда).
Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называют сечением тетраэдра (параллелепипеда).
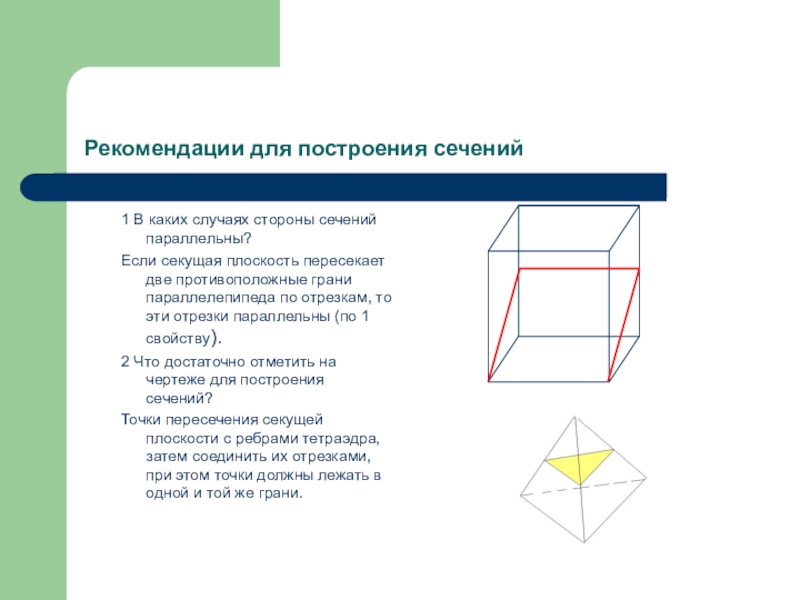
Слайд 5 Рекомендации для построения сечений
1 В каких случаях стороны сечений параллельны?
Если секущая плоскость пересекает две противоположные грани параллелепипеда по отрезкам, то эти отрезки параллельны (по 1 свойству).
2 Что достаточно отметить на чертеже для построения сечений?
Точки пересечения секущей плоскости с ребрами тетраэдра, затем соединить их отрезками, при этом точки должны лежать в одной и той же грани.
Слайд 6Ключевые задачи
Задача №1
Дан куб АВСДА1В1С1Д1. На его ребре ДД1 дана
точка М. Найти точку пересечения прямой С1М плоскостью грани куба АВСД.
Решение: а) точка Х должна принадлежать одновременно плоскостям двух граней АВСД и ВСС1В1, т.е. точка Х должна лежать на линии их пересечения, на прямой ВС. Итак, точка Х должна лежать на прямых ВС и С1М.
Построение: 1. продолжим С1М и ДС до их пересечения в точке Х
2. точка Х–искомая точка пересечения прямой С1М с плоскостью грани куба АВСД.
Решение: а) точка Х должна принадлежать одновременно плоскостям двух граней АВСД и ВСС1В1, т.е. точка Х должна лежать на линии их пересечения, на прямой ВС. Итак, точка Х должна лежать на прямых ВС и С1М.
Построение: 1. продолжим С1М и ДС до их пересечения в точке Х
2. точка Х–искомая точка пересечения прямой С1М с плоскостью грани куба АВСД.
1
1
1
1
Слайд 7Ключевые задачи
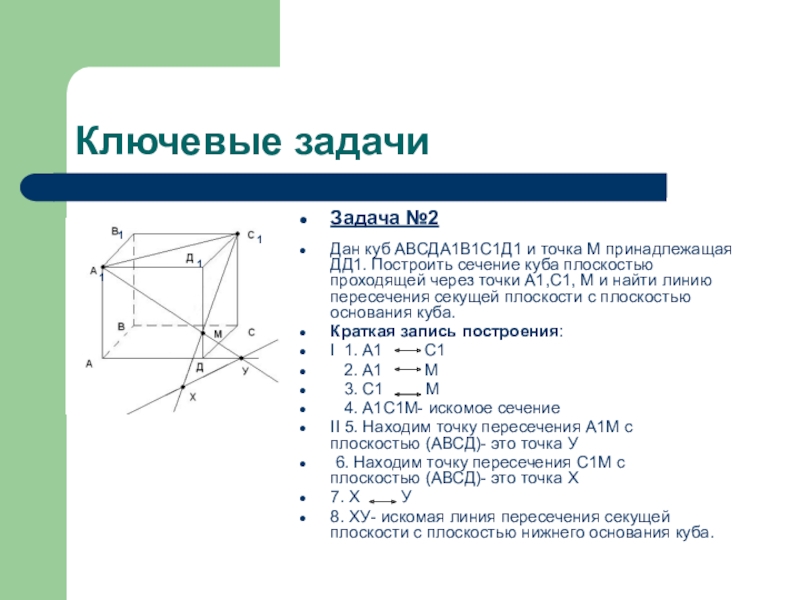
Задача №2
Дан куб АВСДА1В1С1Д1 и точка М принадлежащая ДД1. Построить
сечение куба плоскостью проходящей через точки А1,С1, М и найти линию пересечения секущей плоскости с плоскостью основания куба.
Краткая запись построения:
I 1. А1 С1
2. А1 М
3. С1 М
4. А1С1М- искомое сечение
II 5. Находим точку пересечения А1М с плоскостью (АВСД)- это точка У
6. Находим точку пересечения С1М с плоскостью (АВСД)- это точка Х
7. Х У
8. ХУ- искомая линия пересечения секущей плоскости с плоскостью нижнего основания куба.
Краткая запись построения:
I 1. А1 С1
2. А1 М
3. С1 М
4. А1С1М- искомое сечение
II 5. Находим точку пересечения А1М с плоскостью (АВСД)- это точка У
6. Находим точку пересечения С1М с плоскостью (АВСД)- это точка Х
7. Х У
8. ХУ- искомая линия пересечения секущей плоскости с плоскостью нижнего основания куба.
1
1
1
1
Слайд 8Ключевые задачи
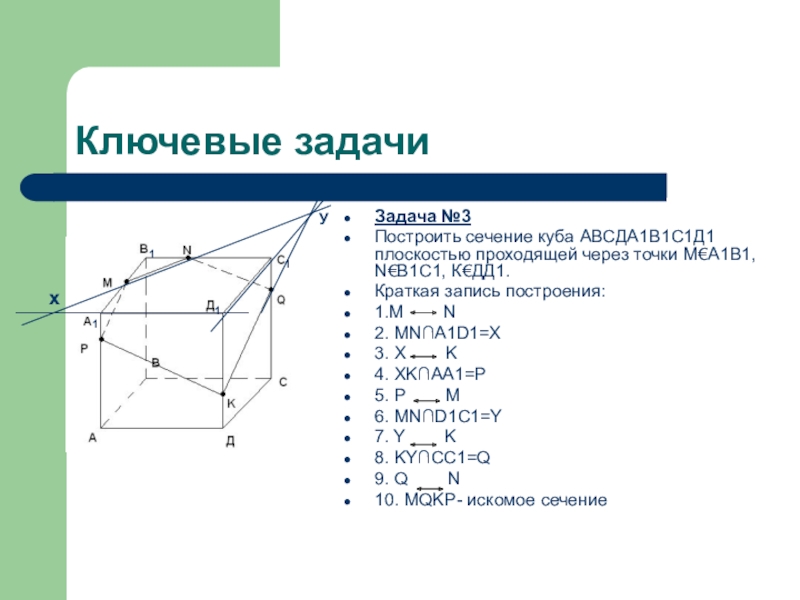
Задача №3
Построить сечение куба АВСДА1В1С1Д1 плоскостью проходящей через точки М€А1В1,
N€В1С1, К€ДД1.
Краткая запись построения:
1.М N
2. MN∩A1D1=X
3. X K
4. XK∩AA1=P
5. P M
6. MN∩D1C1=Y
7. Y K
8. KY∩CC1=Q
9. Q N
10. MQKP- искомое сечение
Краткая запись построения:
1.М N
2. MN∩A1D1=X
3. X K
4. XK∩AA1=P
5. P M
6. MN∩D1C1=Y
7. Y K
8. KY∩CC1=Q
9. Q N
10. MQKP- искомое сечение
У
х
1
1
1
1
Слайд 9Ключевые задачи
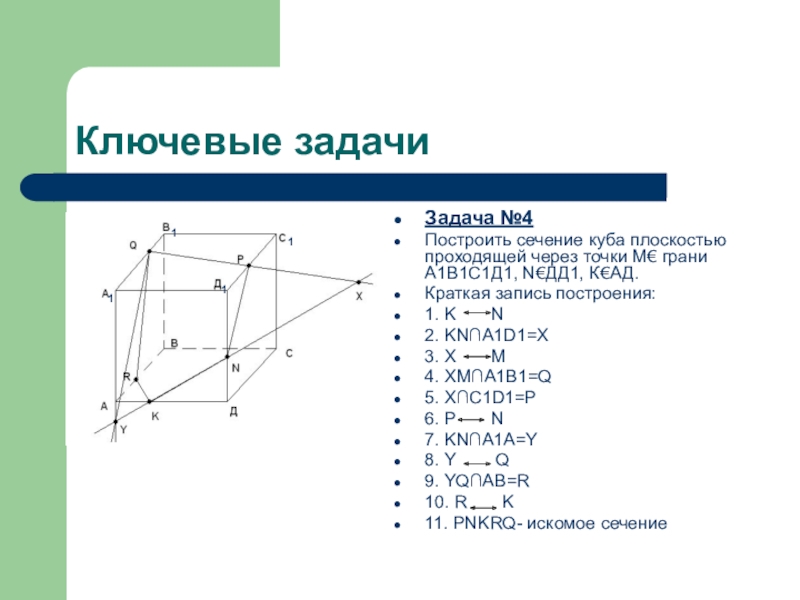
Задача №4
Построить сечение куба плоскостью проходящей через точки М€ грани
А1В1С1Д1, N€ДД1, К€АД.
Краткая запись построения:
1. K N
2. KN∩A1D1=X
3. X M
4. XM∩A1B1=Q
5. X∩C1D1=P
6. P N
7. KN∩A1A=Y
8. Y Q
9. YQ∩AB=R
10. R K
11. PNKRQ- искомое сечение
Краткая запись построения:
1. K N
2. KN∩A1D1=X
3. X M
4. XM∩A1B1=Q
5. X∩C1D1=P
6. P N
7. KN∩A1A=Y
8. Y Q
9. YQ∩AB=R
10. R K
11. PNKRQ- искомое сечение
1
1
1
1
Слайд 10Задания для групп
I (IV) группа
1) Построить сечения куба АВСДА1В1С1Д1 плоскостью, проходящей
через точки А1 , М€Д1С1 и N€ДД1 и найти линию пересечения секущей плоскости с плоскостью нижнего основания куба.
2) Построить сечения куба плоскостью, проходящей через точки М€С1Д1, В1 и N€АД.
3) Построить сечение тетраэдра SABC плоскостью, проходящей через точки: М€SA; N€SC и K€BC.
* Построить сечение куба плоскостью, проходящей через точки на гранях: M€(АА1Д1Д)
N€(А1В1С1Д1)
K€(ДД1С1С).
II (V)группа
Построить сечение куба АВСДА1В1С1Д1 плоскостью, проходящей через точки А1 , М€В1С1 и N€ДД1 и найти линию пересечения секущей плоскости с плоскостью нижнего основания куба
Построить сечения куба плоскостью, проходящей через точки: А1 , М€В1С1, N€АД.
Построить сечение четырёхугольной пирамиды SАВСД плоскостью, проходящей через точки: М€SВ, N€SC, K€AД.
* Построить сечение куба плоскостью, проходящей через точки на гранях: M€(АА1Д1Д)
N€(А1В1С1Д1)
K€(ДД1С1С).
2) Построить сечения куба плоскостью, проходящей через точки М€С1Д1, В1 и N€АД.
3) Построить сечение тетраэдра SABC плоскостью, проходящей через точки: М€SA; N€SC и K€BC.
* Построить сечение куба плоскостью, проходящей через точки на гранях: M€(АА1Д1Д)
N€(А1В1С1Д1)
K€(ДД1С1С).
II (V)группа
Построить сечение куба АВСДА1В1С1Д1 плоскостью, проходящей через точки А1 , М€В1С1 и N€ДД1 и найти линию пересечения секущей плоскости с плоскостью нижнего основания куба
Построить сечения куба плоскостью, проходящей через точки: А1 , М€В1С1, N€АД.
Построить сечение четырёхугольной пирамиды SАВСД плоскостью, проходящей через точки: М€SВ, N€SC, K€AД.
* Построить сечение куба плоскостью, проходящей через точки на гранях: M€(АА1Д1Д)
N€(А1В1С1Д1)
K€(ДД1С1С).
Слайд 11Задания для групп
III (VI)группа
Построить сечение треугольной призмы АВСА1В1С1 плоскостью, проходящей через
точки: М€АС, N€CC1, K€ВВ1.
Построить сечение куба АВСДА1В1С1Д1 плоскостью, проходящей через точки: М€А1В1, N€В1C1, K€СС1
№85 (учебника).
Построить сечение куба АВСДА1В1С1Д1 плоскостью, проходящей через точки: М€А1В1, N€В1C1, K€СС1
№85 (учебника).
Слайд 12Контрольная работа
Контрольная работа (геом.- 10кл.) по теме «Задачи на построение сечений»
Вариант
1- уровень А (слабый)
1)Построить сечение параллелепипеда АВСDA1B1C1D1 плоскостью ,проходящей через середину ребра АВ параллельно плоскости (АСС1).
2)Изобразите тетраэдр АВСD и отметьте точку М на ребре АВ. Постройте сечение, проходящее через точку М параллельно прямым АС и ВD.
3)Решите №83(б)
Вариант 2- уровень А-В
1)Постройте сечение куба плоскостью, проходящей через точки:
М СС1, N DC, K AA1.
2) Постройте сечение четырёхугольной пирамиды SABCD плоскостью, проходящей через точки: M AB, N AS, K BC.
3)Решите №105.
1)Построить сечение параллелепипеда АВСDA1B1C1D1 плоскостью ,проходящей через середину ребра АВ параллельно плоскости (АСС1).
2)Изобразите тетраэдр АВСD и отметьте точку М на ребре АВ. Постройте сечение, проходящее через точку М параллельно прямым АС и ВD.
3)Решите №83(б)
Вариант 2- уровень А-В
1)Постройте сечение куба плоскостью, проходящей через точки:
М СС1, N DC, K AA1.
2) Постройте сечение четырёхугольной пирамиды SABCD плоскостью, проходящей через точки: M AB, N AS, K BC.
3)Решите №105.
Слайд 13Контрольная работа
Вариант 3- уровень А-В
1) Построить сечение куба плоскостью, проходящей через
точки:
M BC, N DC, K AA1.
2) Построить сечение тетраэдра SABC плоскостью, проходящей через точки: M SC, N AC, K SB.
3) Решите №83(а).
Вариант 4- уровень В
1) Постройте сечение куба плоскостью, проходящей через точки:
M BC, N CC1, K AB.
2) Постройте сечение треугольной призмы АВСА1В1С1 плоскостью,
Проходящей через точки: M AC, N A1B1, K BB1.
3) Решите №106.
Вариант 5- уровень В
1) Постройте сечение куба плоскостью, проходящей через точки:M A1B1, N DC, K BC.
2) Постройте сечение треугольной призмы АВСА1В1С1 плоскостью , проходящей через точки: M A1B1, N AC, K BC.
3) Решите №107.
M BC, N DC, K AA1.
2) Построить сечение тетраэдра SABC плоскостью, проходящей через точки: M SC, N AC, K SB.
3) Решите №83(а).
Вариант 4- уровень В
1) Постройте сечение куба плоскостью, проходящей через точки:
M BC, N CC1, K AB.
2) Постройте сечение треугольной призмы АВСА1В1С1 плоскостью,
Проходящей через точки: M AC, N A1B1, K BB1.
3) Решите №106.
Вариант 5- уровень В
1) Постройте сечение куба плоскостью, проходящей через точки:M A1B1, N DC, K BC.
2) Постройте сечение треугольной призмы АВСА1В1С1 плоскостью , проходящей через точки: M A1B1, N AC, K BC.
3) Решите №107.