обучающиеся группы № 14
Головков Алексей,
Дудольский Владимир
Руководитель проекта Грибова О.М.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Математика. Проект на тему Тела вращения.
Содержание
- 1. Презентация по дисциплине Математика. Проект на тему Тела вращения.
- 2. Основные этапы исследовательской работы: 1)
- 3. Актуальность выбранной темы:Мы считаем , что данная
- 4. Цель исследовательской работыИзучить понятие тела вращения;Изучить какие
- 5. Задачи исследовательской работы Узнать историю появления
- 6. Тела вращения — это…Тела вращения — объёмные
- 7. Слайд 7
- 8. Цилиндром называется тело, которое состоит из двух
- 9. Основные элементы цилиндра:• прямой круговой цилиндр - это
- 10. Свойства цилиндра:• основания цилиндра равны, так как параллельный
- 11. Сечения цилиндра:• секущая плоскость проходит вдоль оси цилиндра.
- 12. Э́ллипс— замкнутая кривая на плоскости, которая может
- 13. Эллипсо́ид враще́ния (сфероид) - это фигура вращения
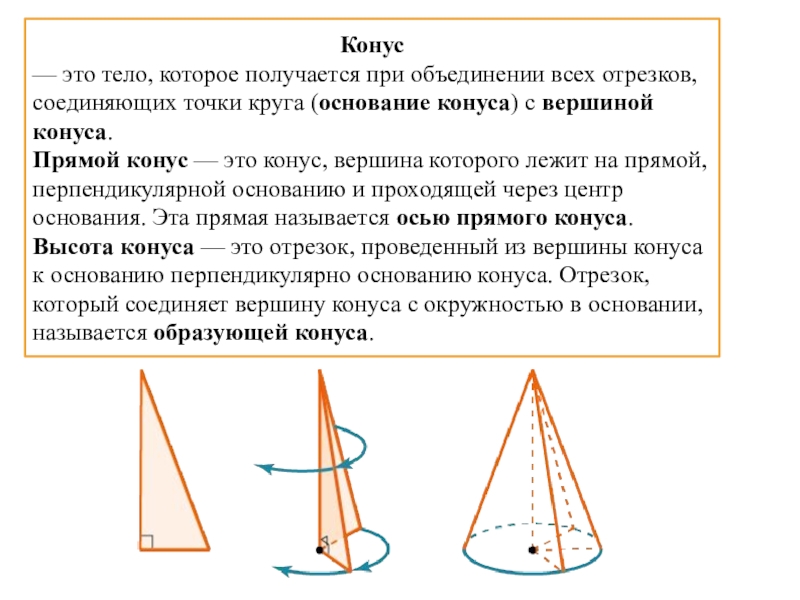
- 14. Конус — это тело, которое получается при
- 15. Осевое сечение. Если сечение конуса проходит через
- 16. Шар - тело, состоящие из всех точек
- 17. Тела вращения или элементы этих тел в архитектурных сооружениях мира, в природе.
- 18. Архитектурные сооружения состоят из отдельных деталей, каждая
- 19. Шар в архитектуреИсаакиевский собор в Санкт - Петербурге
- 20. Шар в природе
- 21. В космическом пространстве
- 22. Конус
- 23. Конус в природе (вершины гор, кроны деревьев, еловые шишки, лишайник – кладония красноплодная)
- 24. Музей – заповедник «Сталинградская битва». г. Волгоград
- 25. В природе мы часто встречаем конуС…
- 26. Ель конусная лесная 20 метров в высоту, диаметр нижнего яруса 8,2 метра
- 27. Цилиндр в природе
- 28. Падающая башня в Италииг. Пиза
- 29. Дом Мельникова — одноквартирный жилой
- 30. Результаты: Мы изучили, что
- 31. Заключение: Математика (геометрия) для творческого
- 32. Выводы: Я считаю, что мы
- 33. Спасибо за внимание!
Основные этапы исследовательской работы: 1) Определение темы проекта.2) Определение цели проекта.3) Определение задач проекта.4) План выполнения проекта.5) Сбор информации.6) Вывод
Слайд 1Проект по дисциплине Математика
Тема: Тела вращения
Использование тел вращения в жизни
Проект выполнили
Слайд 2
Основные этапы исследовательской работы:
1) Определение темы проекта.
2) Определение цели проекта.
3) Определение
задач проекта.
4) План выполнения проекта.
5) Сбор информации.
6) Вывод
4) План выполнения проекта.
5) Сбор информации.
6) Вывод
Слайд 3Актуальность выбранной темы:
Мы считаем , что данная тема проекта актуальна, потому
что она, в первую очередь,
расширяет интересы в области геометрии;
позволяет нам узнать о том, что геометрические фигуры встречаются и окружают нас в нашей повседневной жизни;
многие архитекторы создают проекты будущих сооружений с использованием форм тел вращения.
расширяет интересы в области геометрии;
позволяет нам узнать о том, что геометрические фигуры встречаются и окружают нас в нашей повседневной жизни;
многие архитекторы создают проекты будущих сооружений с использованием форм тел вращения.
Слайд 4Цель исследовательской работы
Изучить понятие тела вращения;
Изучить какие тела вращения существуют и
как они выглядят;
Исследовать архитектуру крупных городов мира и найти в ней элементы тел вращения.
Исследовать архитектуру крупных городов мира и найти в ней элементы тел вращения.
Слайд 5
Задачи исследовательской работы
Узнать историю появления тел вращения;
Распространение тел вращения в природе,
животном и растительном мире;
Использование комбинации тел вращения в архитектуре.
Использование комбинации тел вращения в архитектуре.
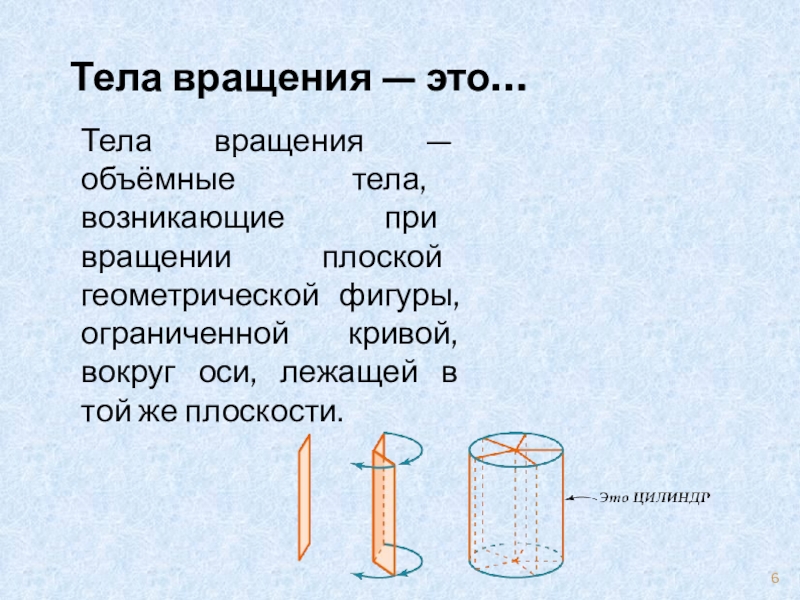
Слайд 6Тела вращения — это…
Тела вращения — объёмные тела, возникающие при вращении
плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.
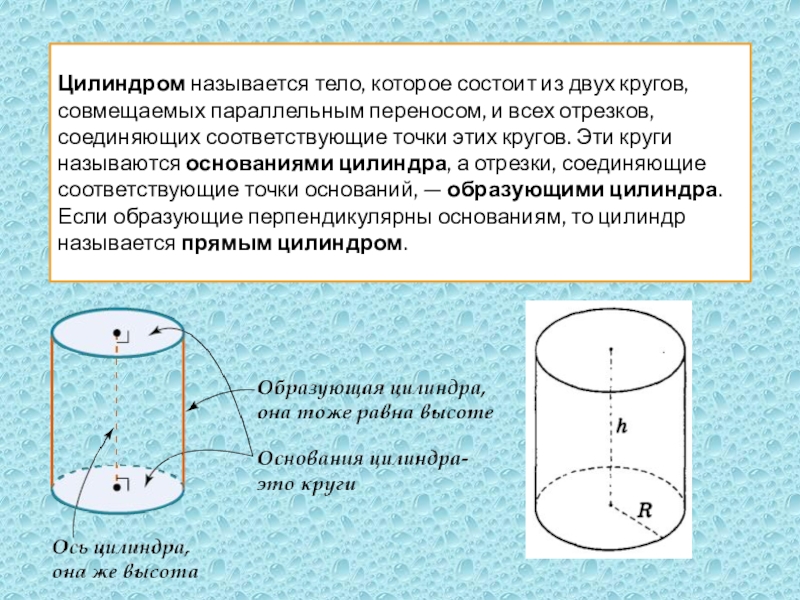
Слайд 8Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом,
и всех отрезков, соединяющих соответствующие точки этих кругов. Эти круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки оснований, — образующими цилиндра.
Если образующие перпендикулярны основаниям, то цилиндр называется прямым цилиндром.
Если образующие перпендикулярны основаниям, то цилиндр называется прямым цилиндром.
Слайд 9Основные элементы цилиндра:
• прямой круговой цилиндр - это тело, получаемое вращением прямоугольника
вокруг одной из его сторон;
• сторона прямоугольника, вокруг которой производилось вращение, называется осью цилиндра;
• радиус основания является радиусом цилиндра;
• расстояние между основаниями цилиндра называется его высотой;
• любой отрезок, параллельный оси цилиндра и соединяющий граничные точки его оснований, называется образующей цилиндра.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
• сторона прямоугольника, вокруг которой производилось вращение, называется осью цилиндра;
• радиус основания является радиусом цилиндра;
• расстояние между основаниями цилиндра называется его высотой;
• любой отрезок, параллельный оси цилиндра и соединяющий граничные точки его оснований, называется образующей цилиндра.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих. Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
Слайд 10Свойства цилиндра:
• основания цилиндра равны, так как параллельный перенос есть движение;
• основания цилиндра
лежат в параллельных плоскостях, так как при параллельном переносе плоскость переходит в параллельную плоскость;
• образующие цилиндра параллельны и равны, так как при параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние.
• образующие цилиндра параллельны и равны, так как при параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние.
Слайд 11Сечения цилиндра:
• секущая плоскость проходит вдоль оси цилиндра. Такое сечение называется осевым;
• секущая
плоскость перпендикулярна оси цилиндра. Сечением является круг;
• секущая плоскость параллельна оси цилиндра. Сечением является прямоугольник;
• секущая плоскость наклонена к плоскости основания. Сечением является эллипс.
• секущая плоскость параллельна оси цилиндра. Сечением является прямоугольник;
• секущая плоскость наклонена к плоскости основания. Сечением является эллипс.
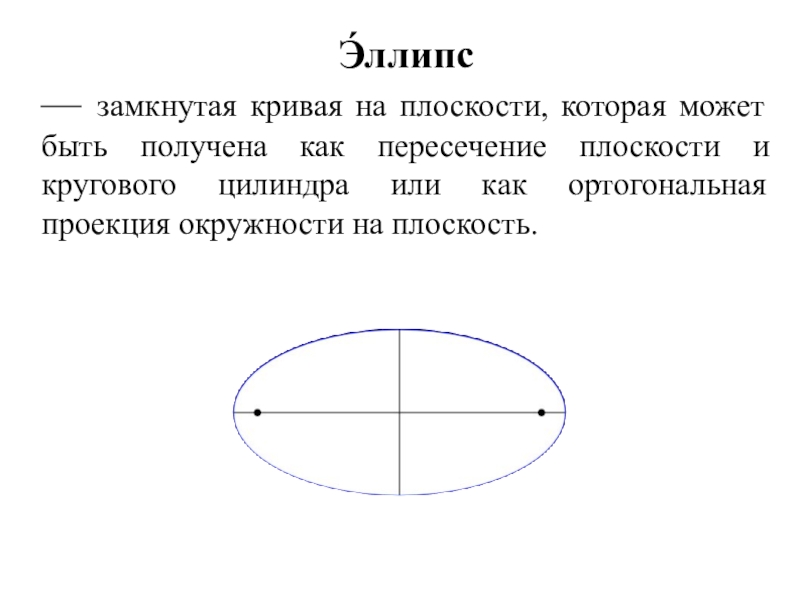
Слайд 12Э́ллипс
— замкнутая кривая на плоскости, которая может быть получена как пересечение
плоскости и кругового цилиндра или как ортогональная проекция окружности на плоскость.
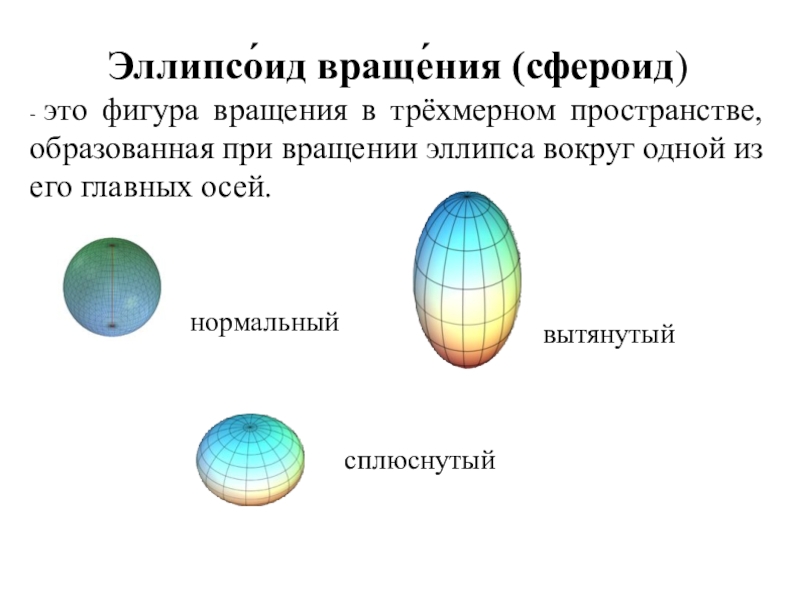
Слайд 13Эллипсо́ид враще́ния (сфероид)
- это фигура вращения в трёхмерном пространстве, образованная
при вращении эллипса вокруг одной из его главных осей.
нормальный
сплюснутый
вытянутый
Слайд 14Конус
— это тело, которое получается при объединении всех отрезков, соединяющих
точки круга (основание конуса) с вершиной конуса.
Прямой конус — это конус, вершина которого лежит на прямой, перпендикулярной основанию и проходящей через центр основания. Эта прямая называется осью прямого конуса.
Высота конуса — это отрезок, проведенный из вершины конуса к основанию перпендикулярно основанию конуса. Отрезок, который соединяет вершину конуса с окружностью в основании, называется образующей конуса.
Прямой конус — это конус, вершина которого лежит на прямой, перпендикулярной основанию и проходящей через центр основания. Эта прямая называется осью прямого конуса.
Высота конуса — это отрезок, проведенный из вершины конуса к основанию перпендикулярно основанию конуса. Отрезок, который соединяет вершину конуса с окружностью в основании, называется образующей конуса.
Слайд 15Осевое сечение.
Если сечение конуса проходит через ось конуса, то сечение
представляет собой равнобедренный треугольник, основание которого - диаметр основания конуса, а боковые стороны - образующие конуса.
• Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг с центром, расположенным на оси конуса.
• Если секущая плоскость перпендикулярна к оси конуса, то сечение конуса представляет собой круг с центром, расположенным на оси конуса.
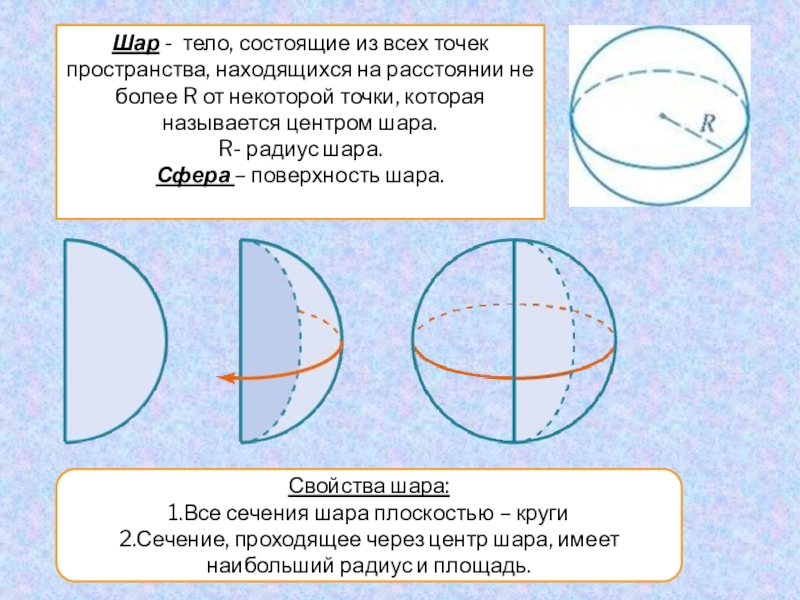
Слайд 16Шар - тело, состоящие из всех точек пространства, находящихся на расстоянии
не более R от некоторой точки, которая называется центром шара.
R- радиус шара.
Сфера – поверхность шара.
R- радиус шара.
Сфера – поверхность шара.
Свойства шара:
1.Все сечения шара плоскостью – круги
2.Сечение, проходящее через центр шара, имеет наибольший радиус и площадь.
Слайд 18Архитектурные сооружения состоят из отдельных деталей, каждая из которых строится на
базе определенных геометрических фигур либо на их комбинации. Кроме того, форма любого архитектурного сооружения имеет своей моделью определенную геометрическую фигуру. «Архитектурная" геометрия наполнена собственным эстетическим содержанием. Выбор использования той или иной фигуры в архитектурном сооружении зависит от множества факторов: эстетичного внешнего вида здания, его прочности, удобства в эксплуатации и т. д. Основные требования к архитектурным сооружениям, сформулированные древнеримским теоретиком архитектуры Витрувием, звучат так: «прочность, польза, красота».
Слайд 22 Конус в архитектуре
Адмиралтейство в Санкт
- Петербурге
Петропавловская крепость в Санкт - Петербурге
Слайд 23Конус в природе (вершины гор, кроны деревьев, еловые шишки, лишайник –
кладония красноплодная)
Слайд 25В природе мы часто встречаем конуС…
Например, в песчаной
пустыне Сахаре, где сами холмы представляют собой конус
Слайд 29Дом Мельникова —
одноквартирный жилой дом, всемирно известный памятник
архитектуры советского авангарда. Был построен в 1927—1929 годах в Кривоарбатском преулке в Москве по проекту выдающегося советского архитектора Константина Мельникова для себя и своей семьи.
Слайд 30
Результаты:
Мы изучили, что же такое тела вращения.
Мы узнали, какие существуют тела
вращения.
Мы изучили их понятия и определения.
Мы исследовали архитектуру многих архитектурных сооружений, выяснили из каких тел вращения они состоят. Думаю, что нам это пригодится в жизни.
Мы изучили их понятия и определения.
Мы исследовали архитектуру многих архитектурных сооружений, выяснили из каких тел вращения они состоят. Думаю, что нам это пригодится в жизни.
Слайд 31
Заключение:
Математика (геометрия) для творческого труда архитектора издавна признается очень важной и
необходимой. Без знаний геометрии нельзя создать ни одного крепкого, прочного и долговечного архитектурного сооружения. А для этого нужно много знать и по геометрии и о строительных материалах. Надо быть хорошим специалистом. Создавать такие архитектурные сооружения, которые будут стоят веками. Ведь и до наших дней дошли сооружения средних веков. Значит, умели строить в Древнем Риме!
На языке архитектуры, можно сказать, что геометрия – это грандиозное сооружение, которое моделирует окружающий нас мир и происходящие в нем явления. Мы пронаблюдали, как геометрия помогает добиться прочности, удобства, красоты архитектурных сооружений.
Также было совершенно доказано, что геометрия является основой и «оформлением» строительной деятельности.
На языке архитектуры, можно сказать, что геометрия – это грандиозное сооружение, которое моделирует окружающий нас мир и происходящие в нем явления. Мы пронаблюдали, как геометрия помогает добиться прочности, удобства, красоты архитектурных сооружений.
Также было совершенно доказано, что геометрия является основой и «оформлением» строительной деятельности.
Слайд 32
Выводы:
Я считаю, что мы справились с теми задачами и целями, которые
были поставлены в начале нашего проекта.
Мы изучили всю ту информацию, которая была необходима, интересна.
Было интересно узнать, что лежит в основе архитектурных сооружений
Мы изучили всю ту информацию, которая была необходима, интересна.
Было интересно узнать, что лежит в основе архитектурных сооружений