- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Площади плоских фигур
Содержание
- 1. Презентация Площади плоских фигур
- 2. Площадь многоугольникаПлощадь квадратаПлощадь квадрата Площадь прямоугольникаПлощадь
- 3. Понятие площадиПлощадь греч. слово plateia – «широкая».
- 4. Площадь – положительное число, которое показывает сколько
- 5. Слайд 5
- 6. Площадь многоугольникаПлощадь многоугольника – это величина той части плоскости, которую занимает многоугольник.1 см1 см
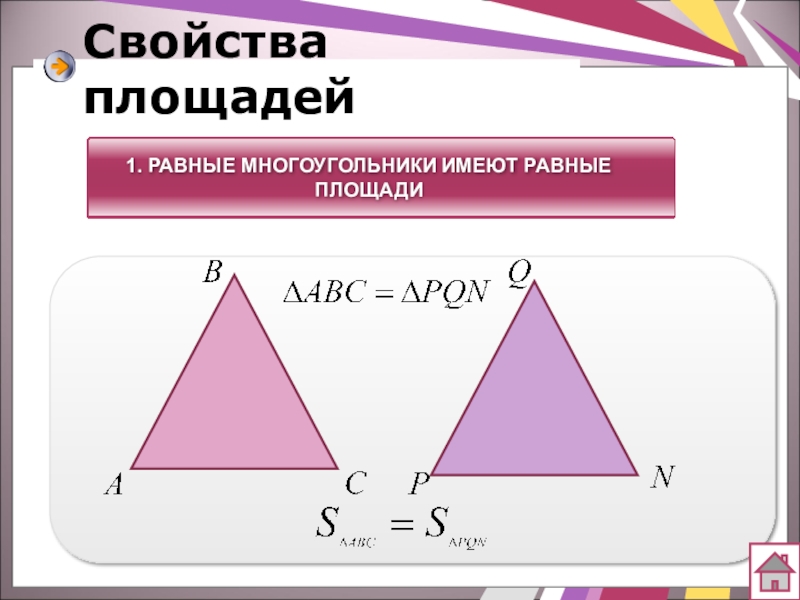
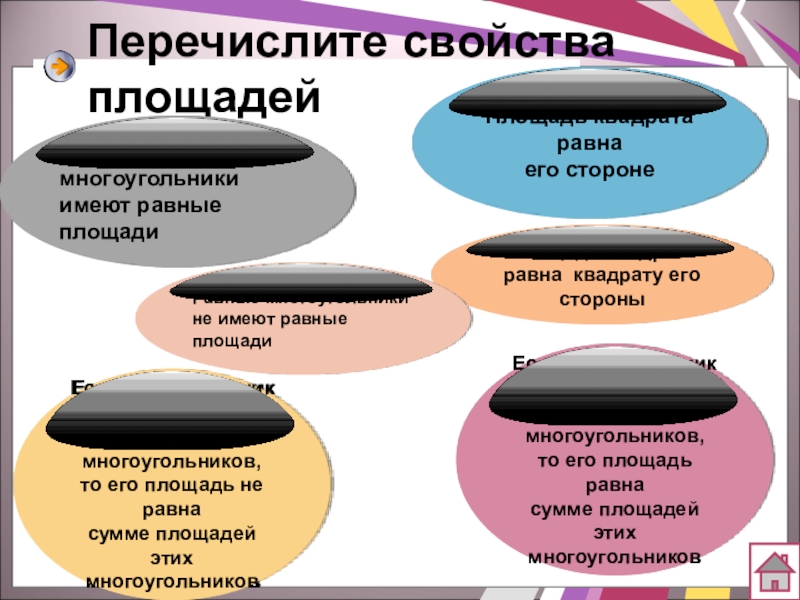
- 7. Свойства площадей1. РАВНЫЕ МНОГОУГОЛЬНИКИ ИМЕЮТ РАВНЫЕ ПЛОЩАДИ
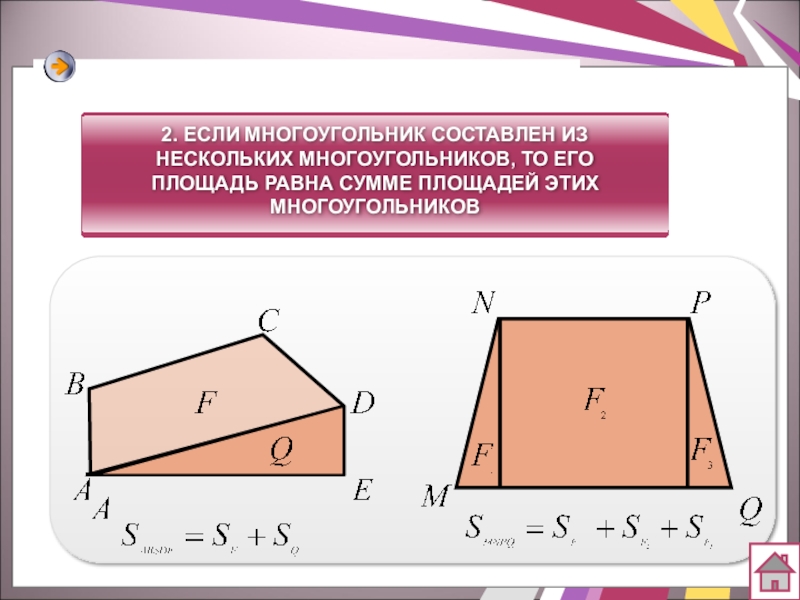
- 8. 2. ЕСЛИ МНОГОУГОЛЬНИК СОСТАВЛЕН ИЗ НЕСКОЛЬКИХ МНОГОУГОЛЬНИКОВ, ТО ЕГО ПЛОЩАДЬ РАВНА СУММЕ ПЛОЩАДЕЙ ЭТИХ МНОГОУГОЛЬНИКОВ
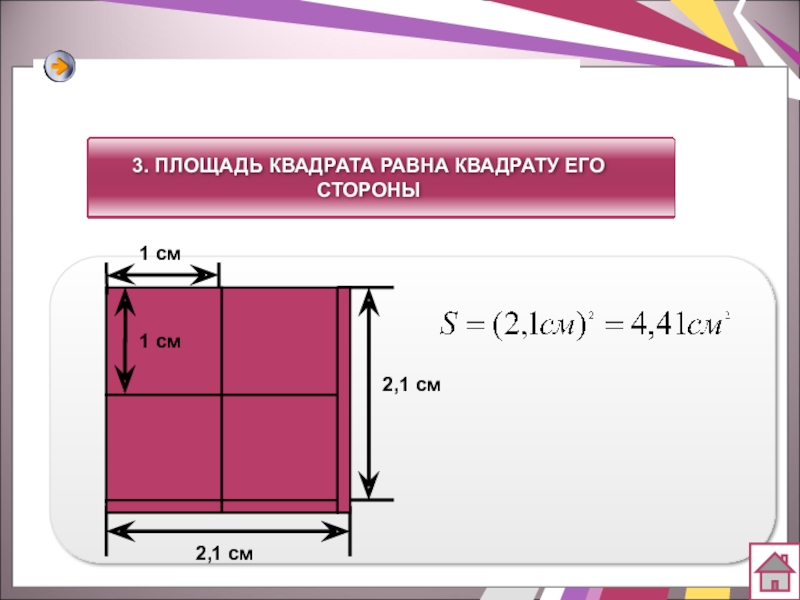
- 9. 3. ПЛОЩАДЬ КВАДРАТА РАВНА КВАДРАТУ ЕГО СТОРОНЫ2,1 см2,1 см1 см1 см
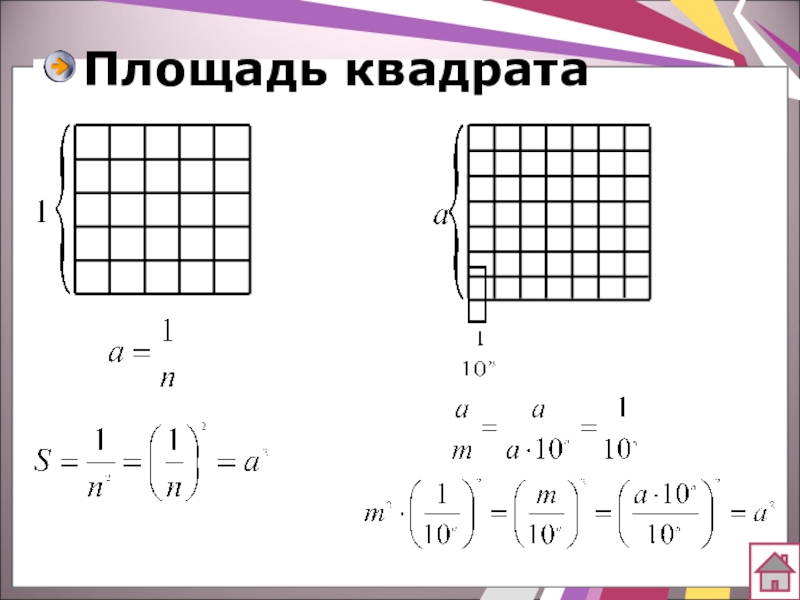
- 10. Площадь квадрата
- 11. Теорема Площадь прямоугольника равна произведению его смежных сторонПлощадь прямоугольникаSba
- 12. aaaabbbba2b2SSДано:ABCD-прямоугольник, AB=b,
- 13. Перечислите свойства площадей
- 14. Площадь параллелограммаТеорема Площадь параллелограмма равна произведению его основания на высотуАBCD
- 15. АBCD12KHДано: ABCD-параллелограмм Доказать: S=AD ·
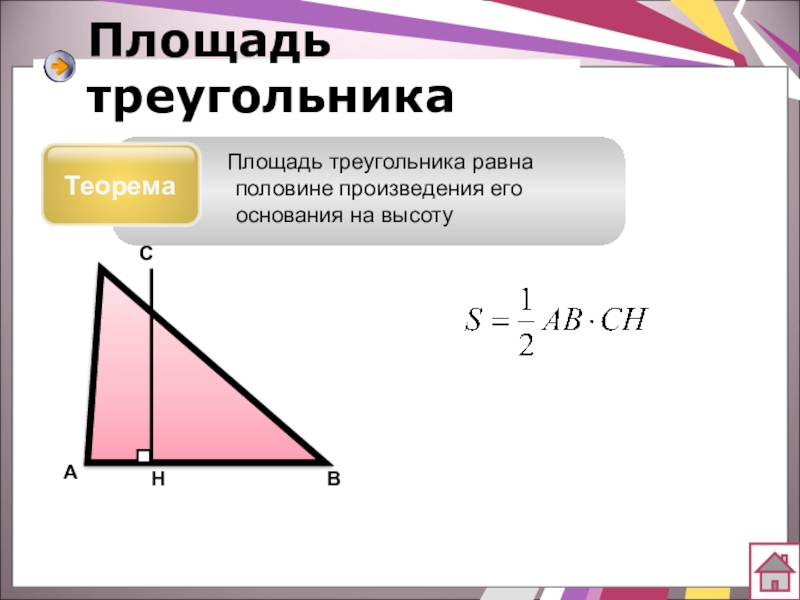
- 16. Площадь треугольникаТеорема Площадь треугольника равна половине произведения его основания на высотуАВСН
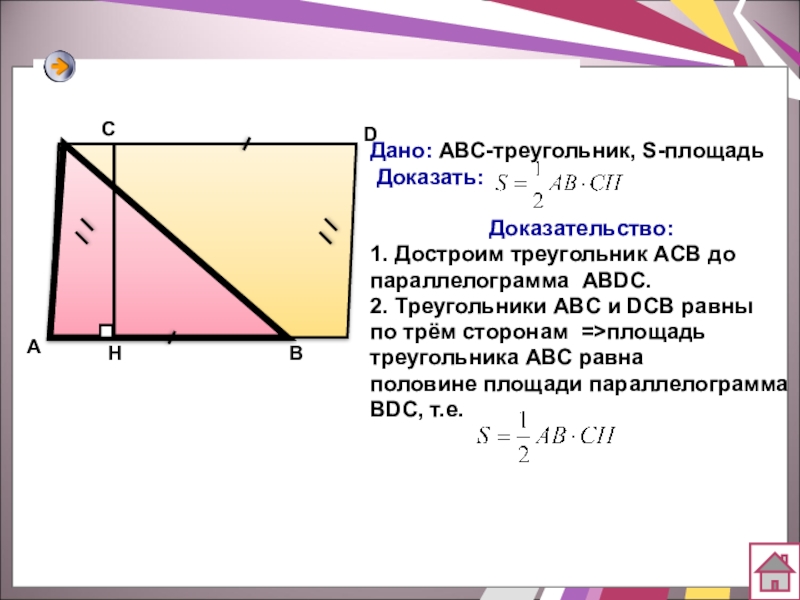
- 17. АВСD.Дано: АВС-треугольник, S-площадь Доказать:
- 18. 200520062072008Если высоты двух треугольников равны, то их
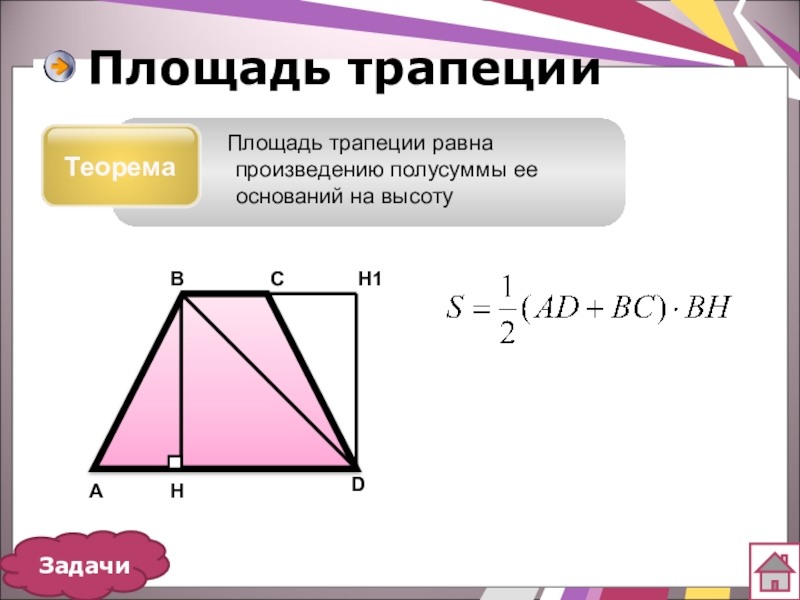
- 19. Площадь трапецииТеорема Площадь трапеции равна произведению полусуммы ее оснований на высоту АBCDHH1Задачи
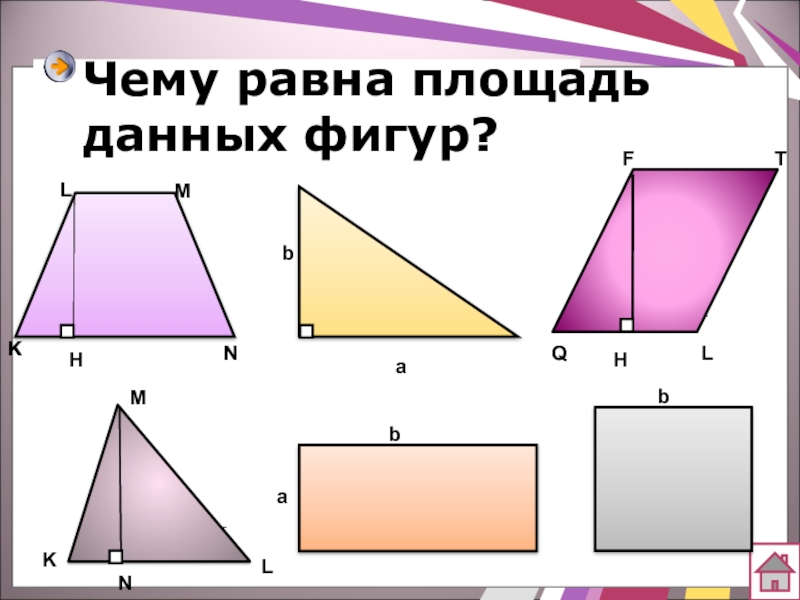
- 20. Чему равна площадь данных фигур?N
- 21. Площадь кругаА1А2А3АnRrnOПлощадь кругового сектора равна
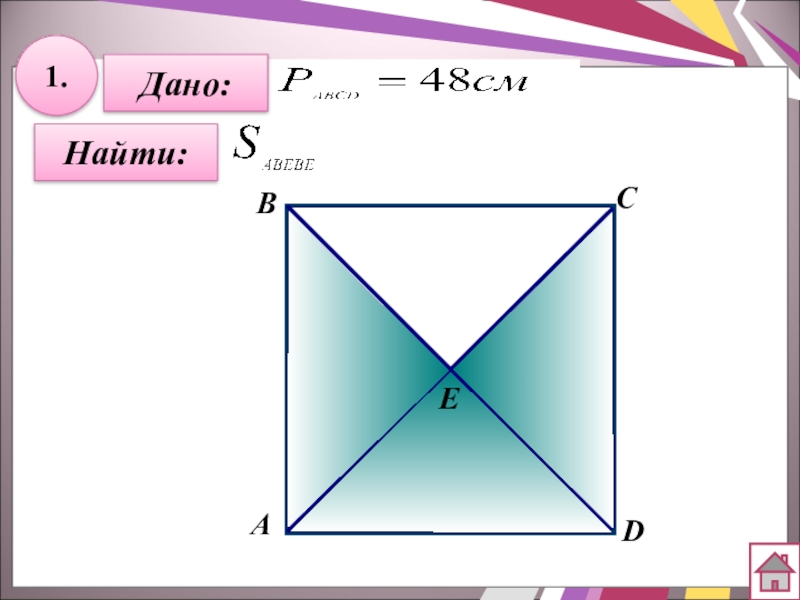
- 22. 1.Дано:АBCDНайти:Е
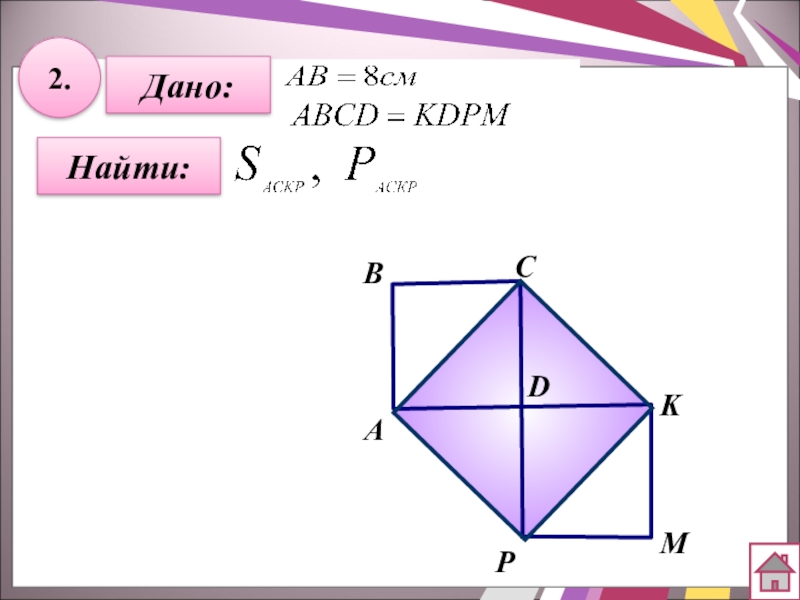
- 23. 2.Дано:Найти:АBCPDMK
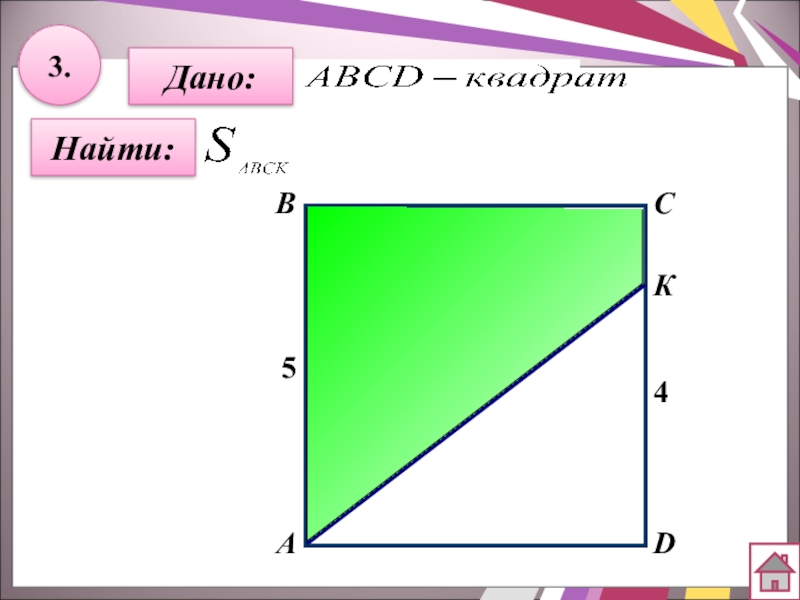
- 24. 3.Найти:АBCDДано:45К
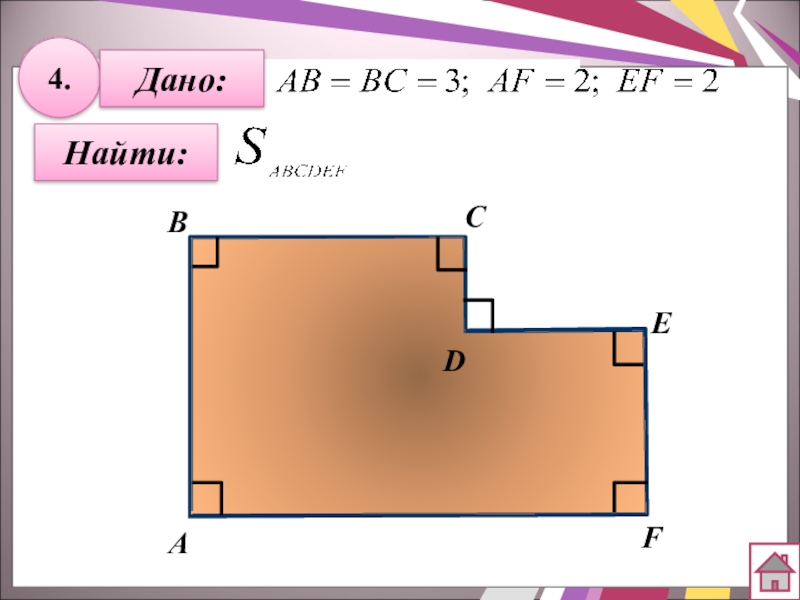
- 25. 4.Дано:Найти:ВАСЕDF
- 26. 5.Дано:АBТDМРКСНайти:
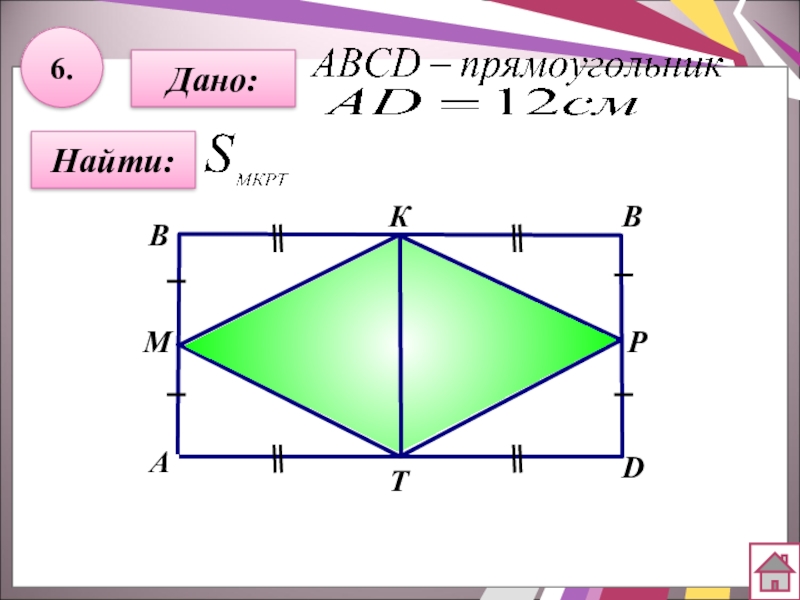
- 27. 6.Найти:Дано:АBКТDВМР
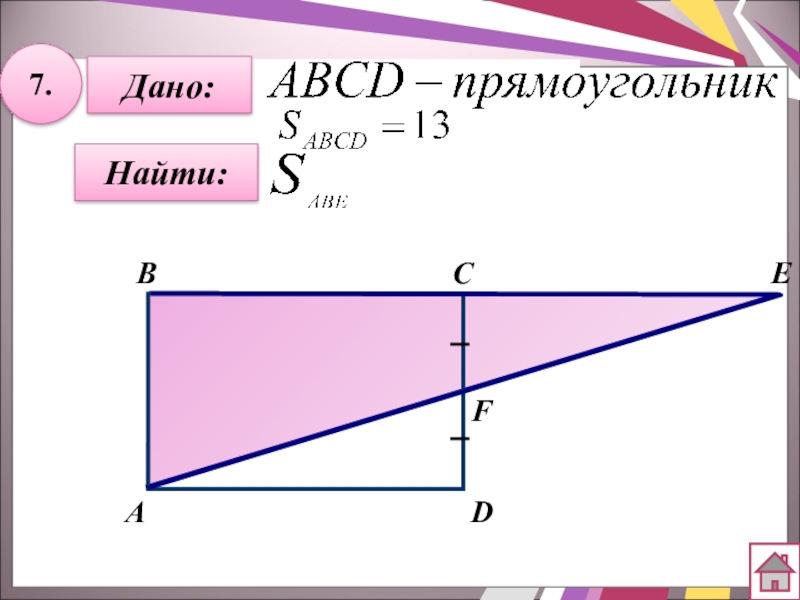
- 28. 7.Дано:СВНайти:АDEF
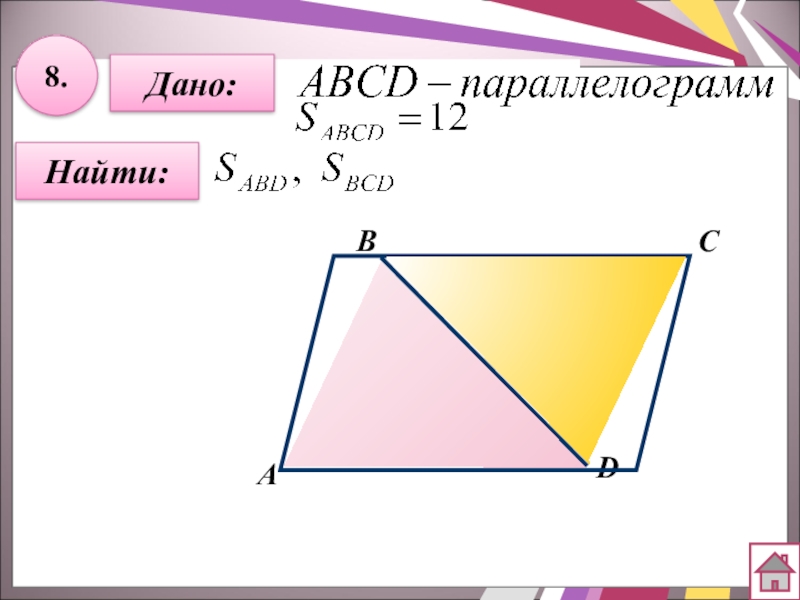
- 29. 8.Найти:DСВАДано:
- 30. 9.Найти:Дано:АBCКDМОР
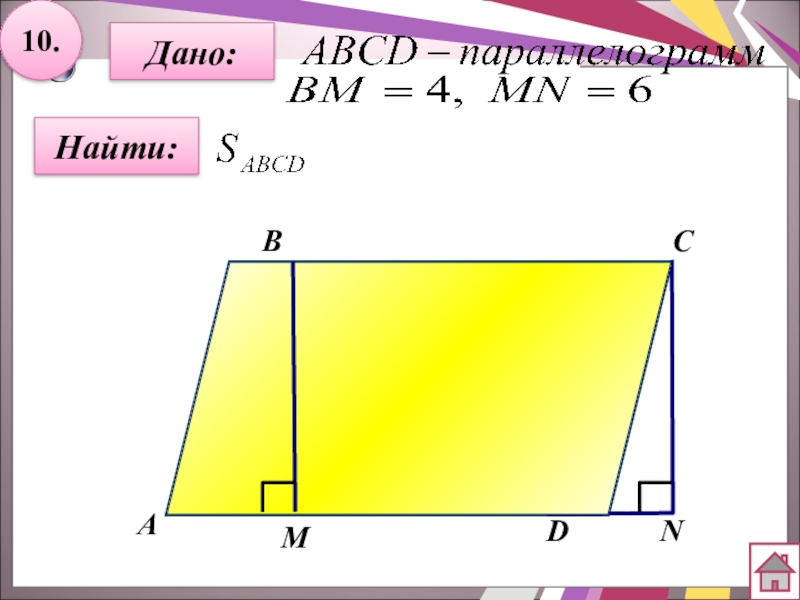
- 31. 10.Дано:Найти:АBCNМD
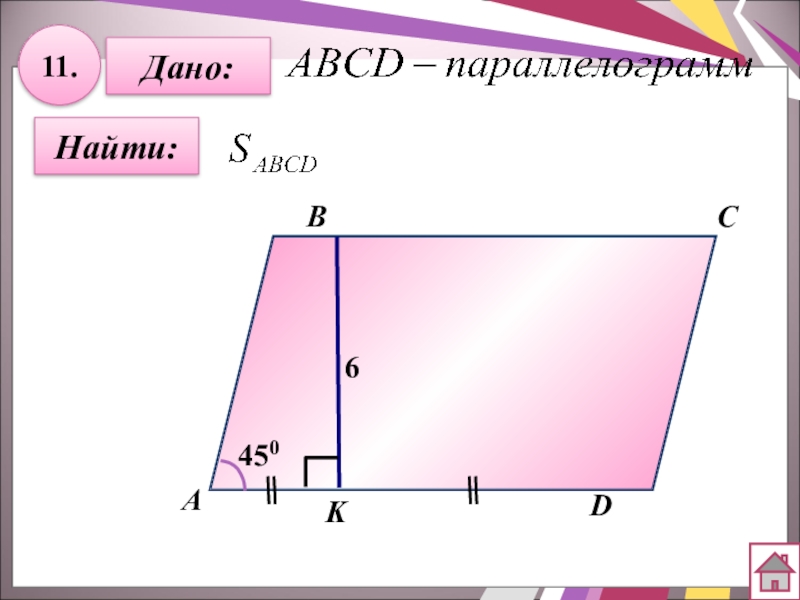
- 32. 11.Найти:Дано:АBCDK6450
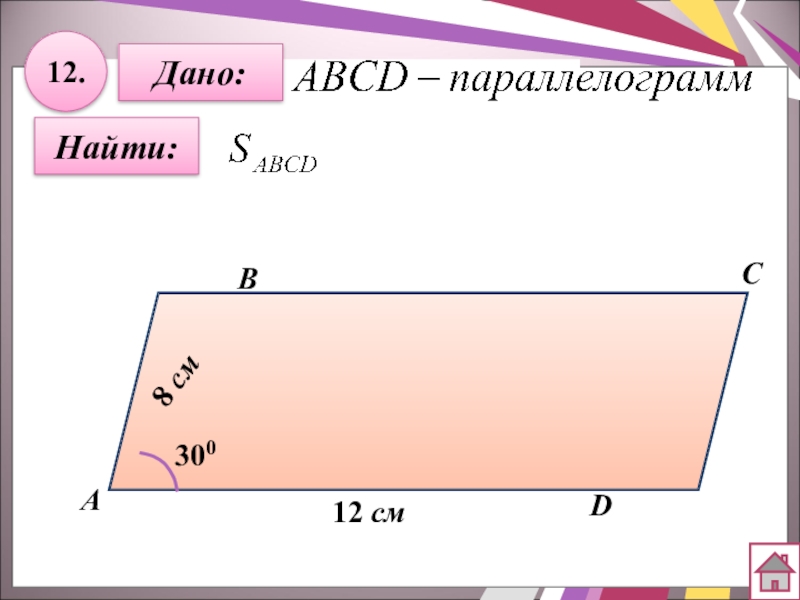
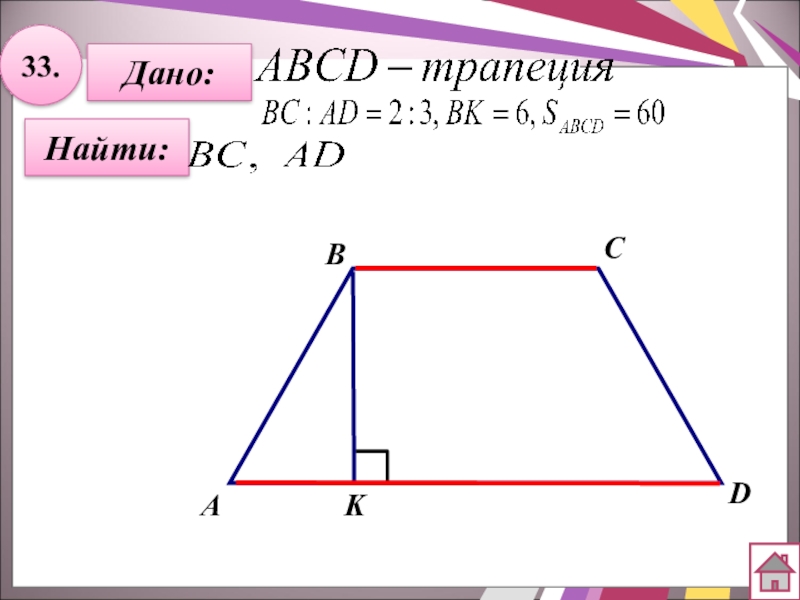
- 33. 12.Найти:Дано:АBCD12 см3008 см
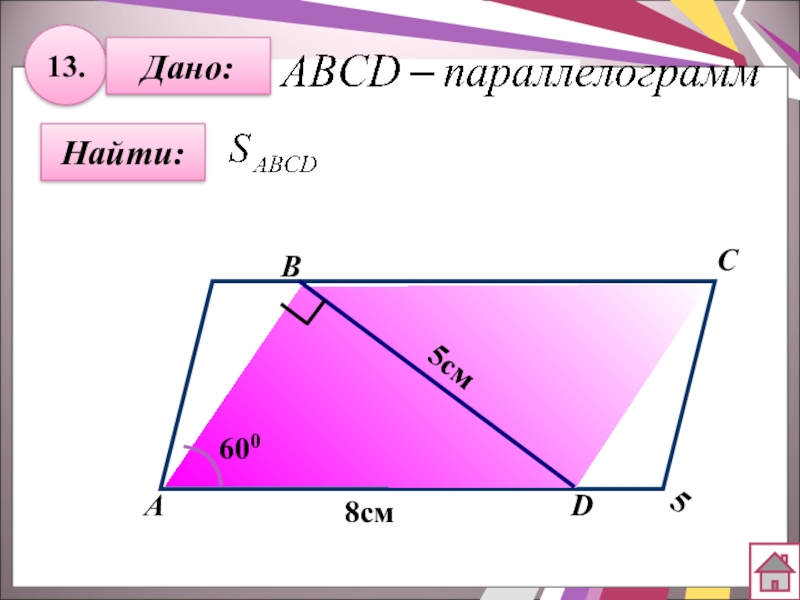
- 34. 13.Найти:Дано:АBCD8см5 5см600
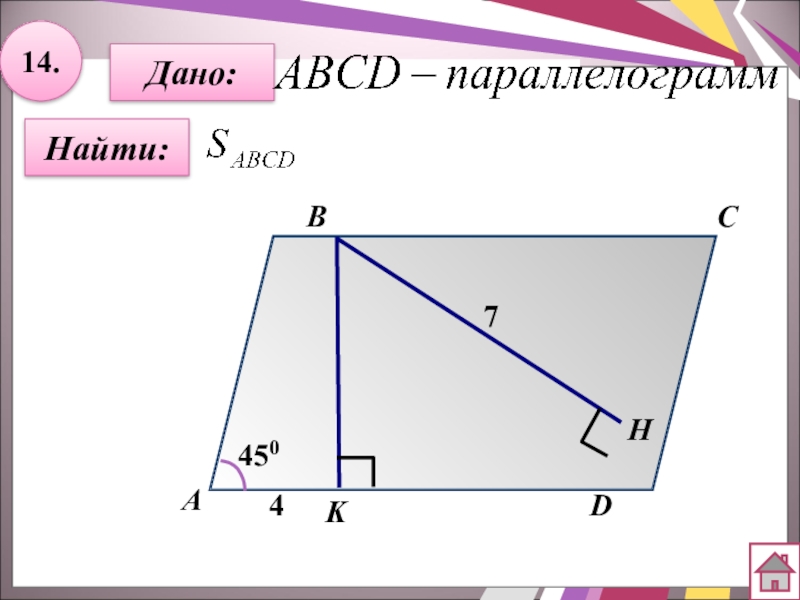
- 35. 14.Дано:АBCDK44507ННайти:
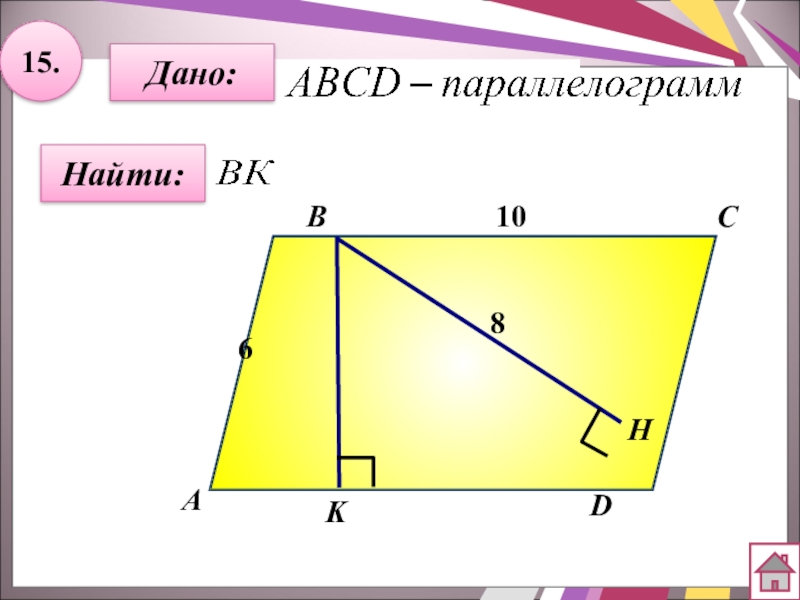
- 36. 15.Дано:АBCDK10ННайти:68
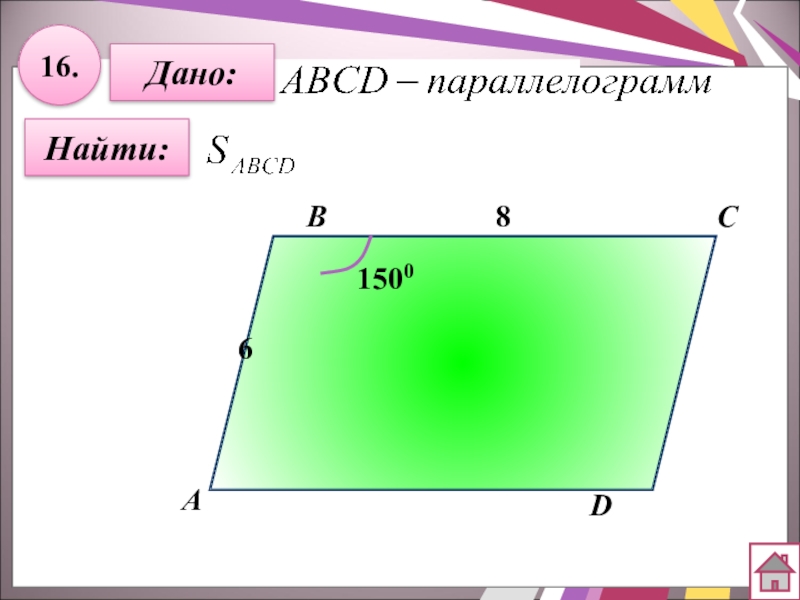
- 37. 16.Дано:АBCD8Найти:61500
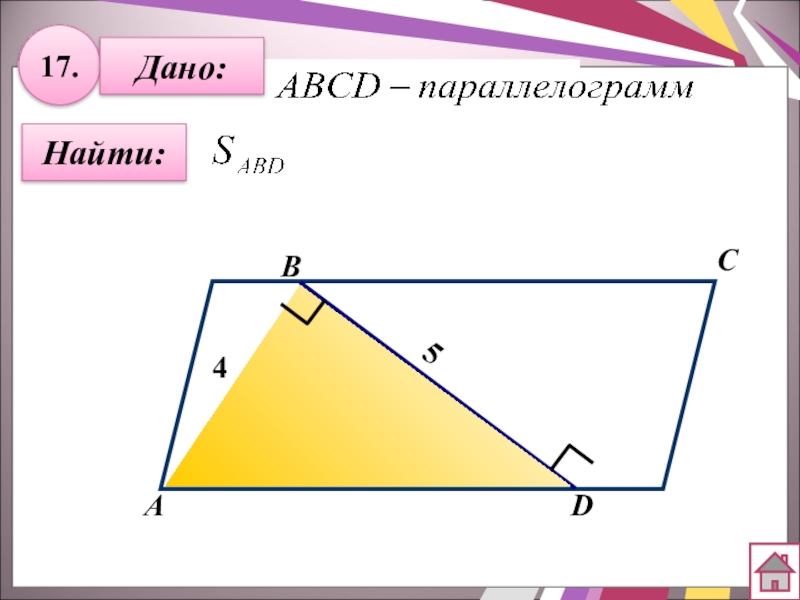
- 38. 17.Найти:Дано:АBCD45
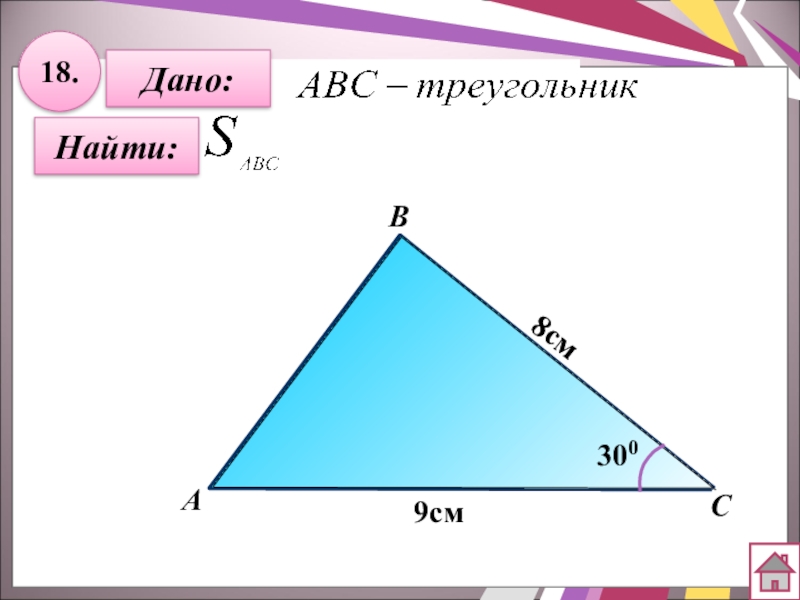
- 39. 18.Найти:Дано:BСА8см 9см 300
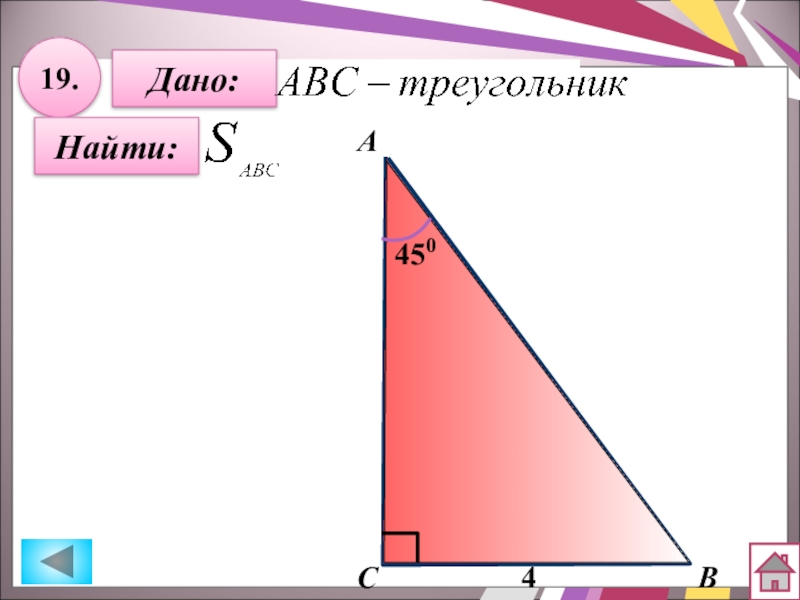
- 40. 19.Найти:Дано:BСА4450
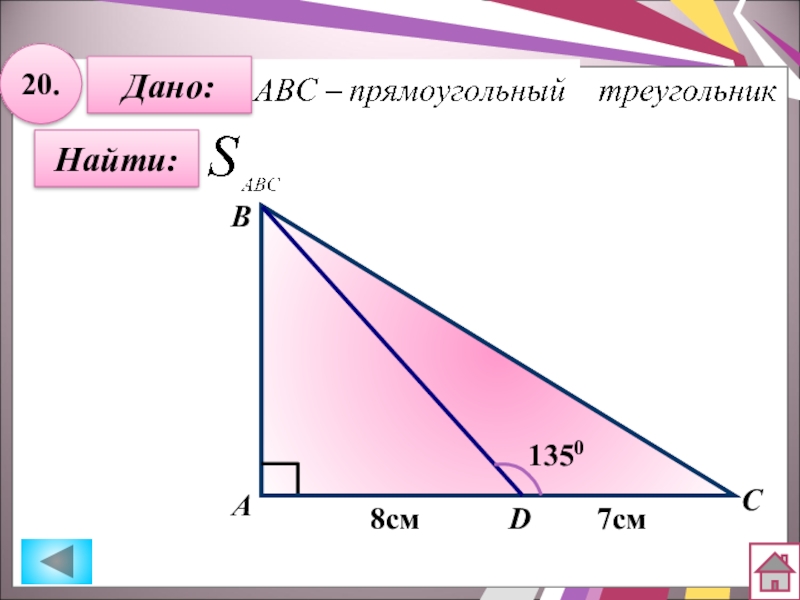
- 41. 20.Найти:Дано:АBCD13508см7см
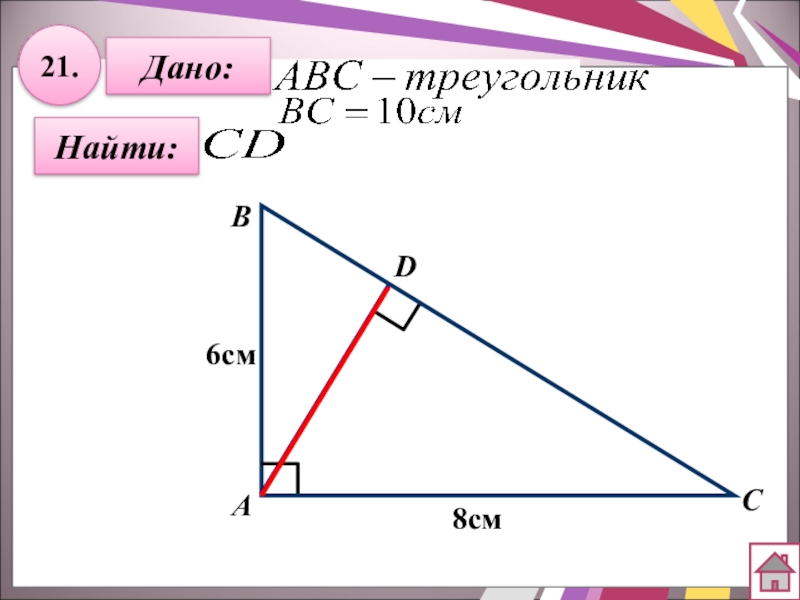
- 42. 21.Найти:Дано:АBCD8см6см
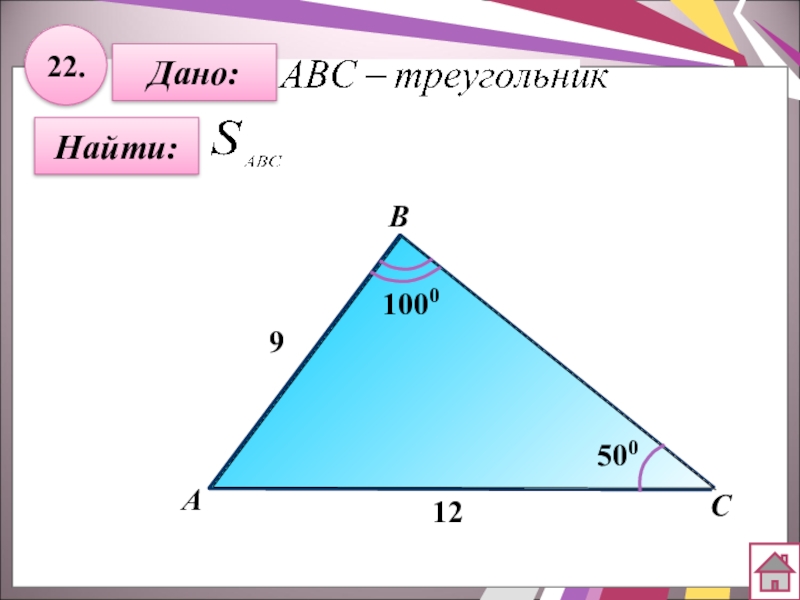
- 43. 22.Найти:Дано:BСА12 50010009
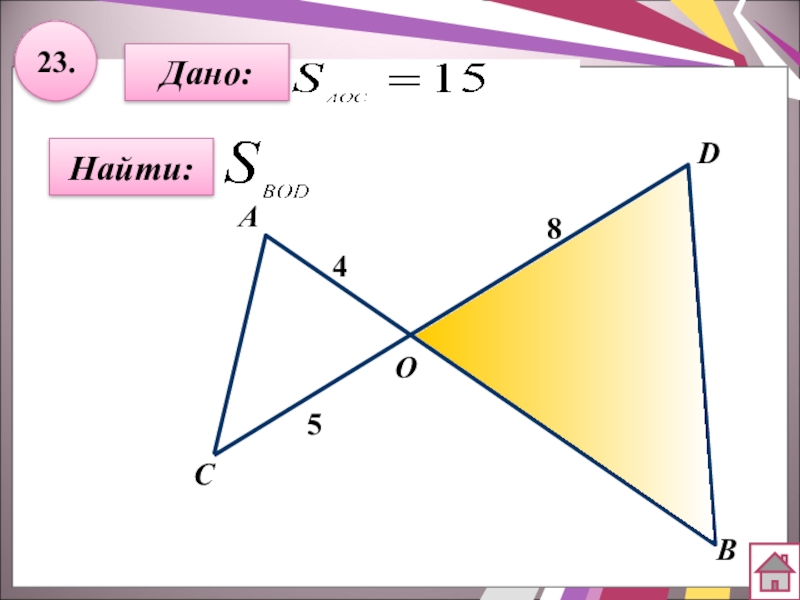
- 44. 23.Найти:АBC8DОДано:45
- 45. 24.Найти:АBCDОДано:
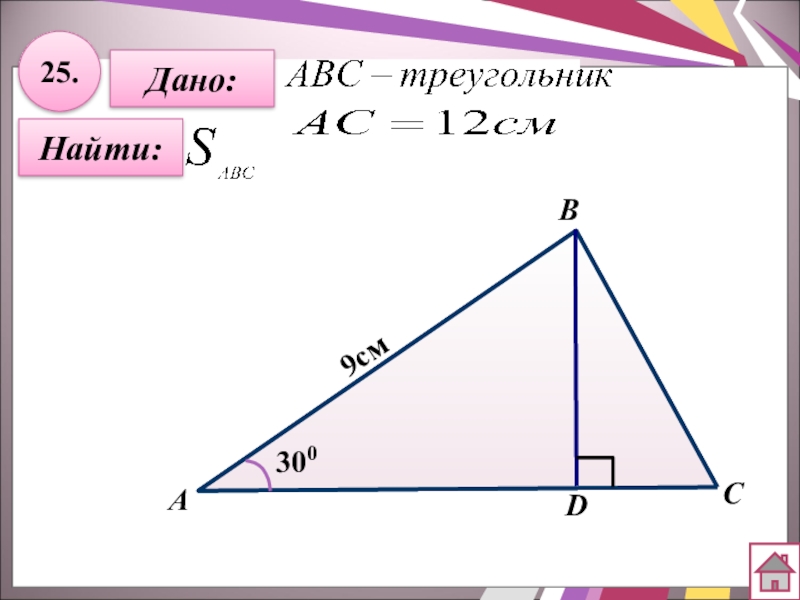
- 46. 25.Найти:АBC9смDДано:300
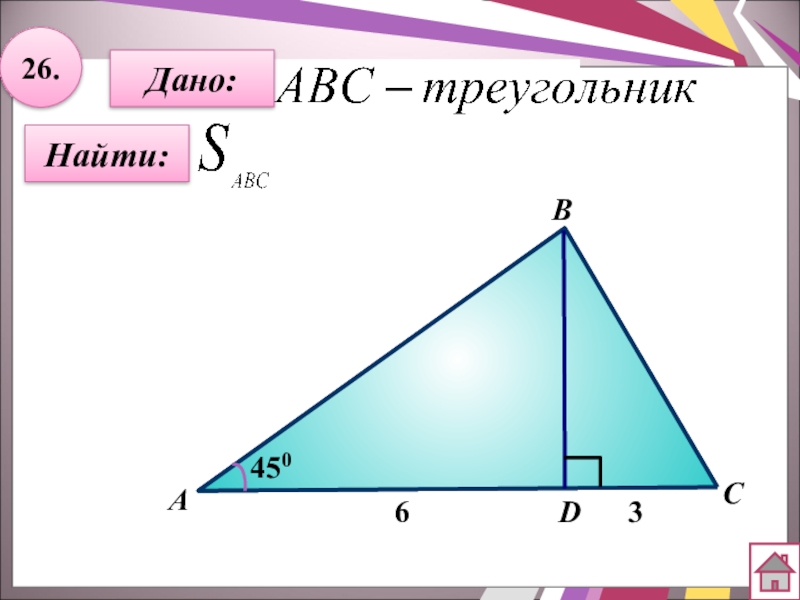
- 47. 26.Найти:Дано:АBCD45063
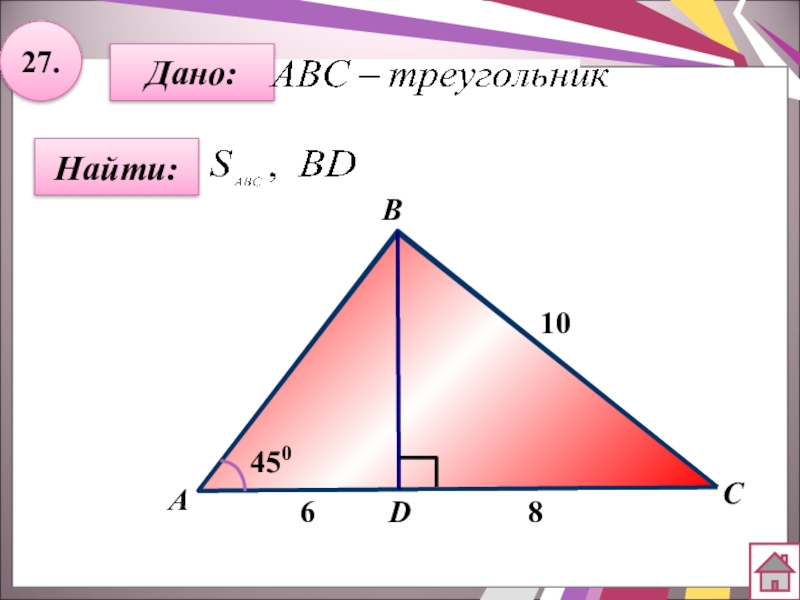
- 48. 27.Найти:Дано:АBC10D45068
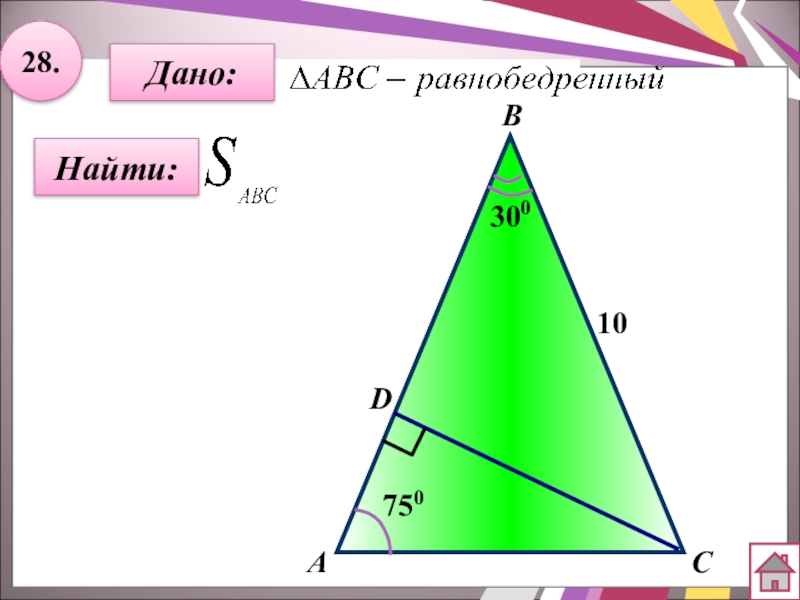
- 49. 28.Найти:Дано:АCВD75030010
- 50. 29.Найти:Дано:АCВ75012750
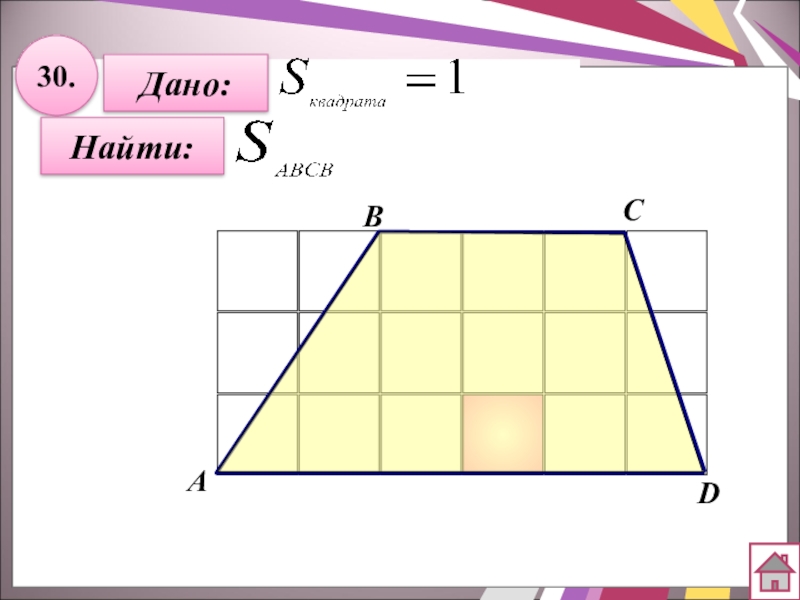
- 51. 30.Дано:Найти:АBCD
- 52. 31.Найти:АBCDДано:7610
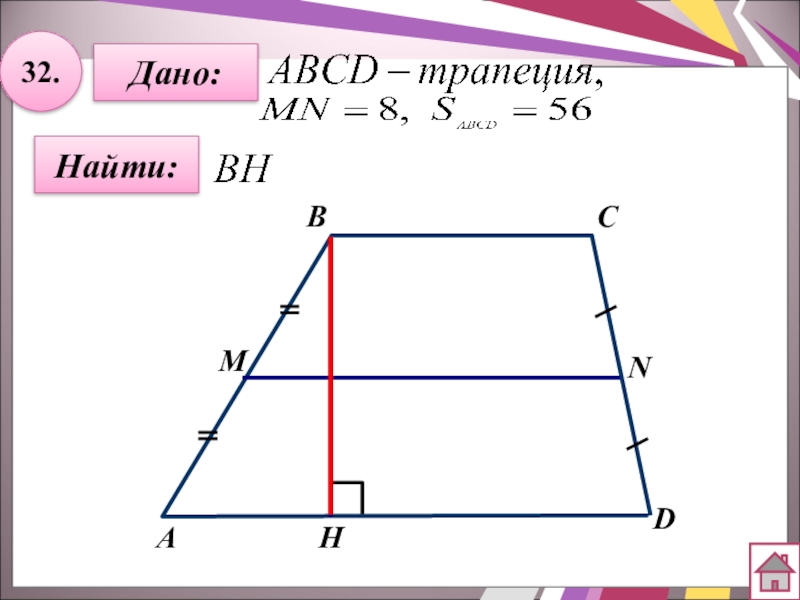
- 53. 32.Найти:Дано:АBCDHMN
- 54. 33.Найти:АBCDДано:K
- 55. Дополнительные заданияНайдите периметр прямоугольника, если его площадь
- 56. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 8 и 18Задание 212141610
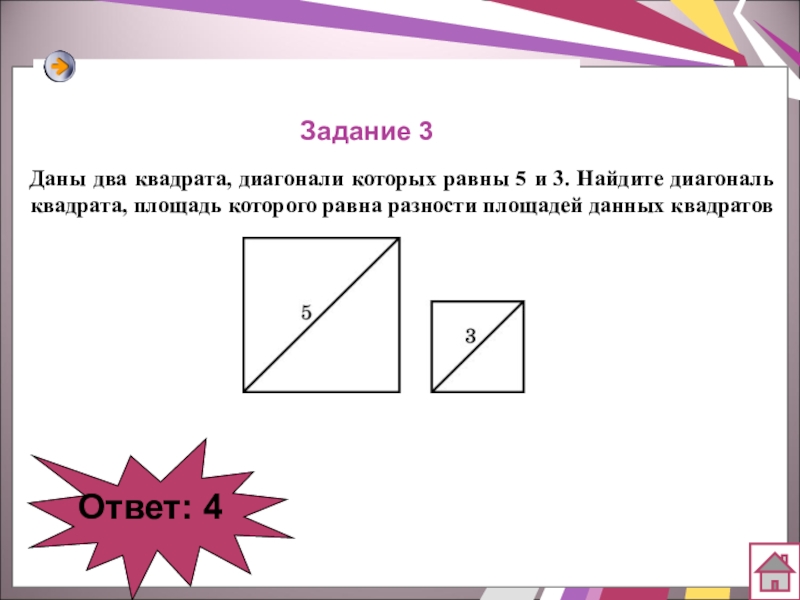
- 57. Задание 3Даны два квадрата, диагонали которых равны
- 58. Стороны параллелограмма равны 15 и 9. Высота,
- 59. Найдите площадь треугольника, две стороны которого равны
- 60. Угол при вершине, противолежащей основанию равнобедренного треугольника,
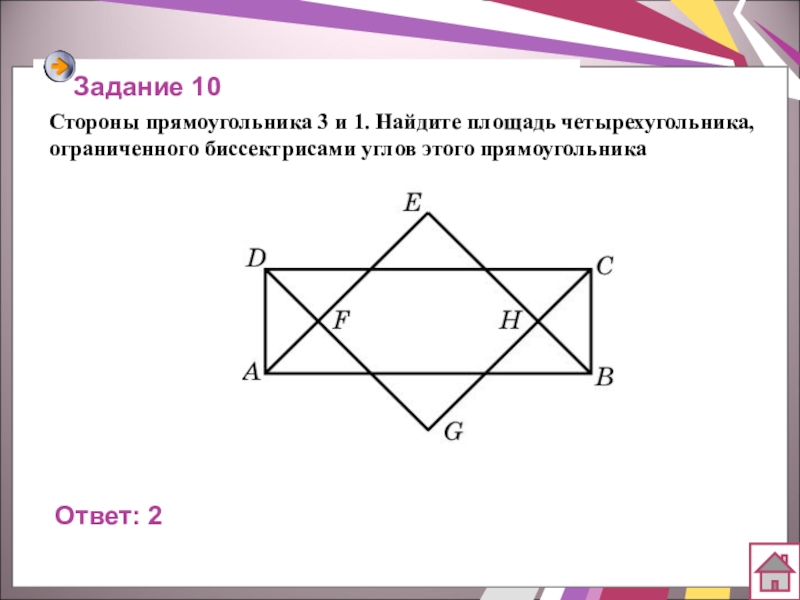
- 61. Стороны прямоугольника 3 и 1. Найдите площадь четырехугольника, ограниченного биссектрисами углов этого прямоугольникаЗадание 10Ответ: 2
- 62. Впишите формулы
- 63. Слайд 63
Площадь многоугольникаПлощадь квадратаПлощадь квадрата Площадь прямоугольникаПлощадь прямоугольника Площадь параллелограммаПлощадь параллелограмма 4123Площадь треугольника5Площадь трапецииПлощадь трапеции Площадь кругаПлощадь круга 67Понятие площади0
Слайд 2Площадь многоугольника
Площадь квадратаПлощадь квадрата
Площадь прямоугольникаПлощадь прямоугольника
Площадь параллелограммаПлощадь
параллелограмма
4
1
2
3
Площадь треугольника
5
Площадь трапецииПлощадь трапеции
Площадь кругаПлощадь круга
6
7
Понятие площади
0
Слайд 3Понятие площади
Площадь греч. слово plateia – «широкая». Происхождение неясно. Некоторые ученые
считают заимств. из ст.-сл. Другие толкуют как исконно русское.
Слайд 4
Площадь – положительное число, которое показывает сколько раз единица измерения или
ее часть укладывается в данной фигуре.
Слайд 6Площадь многоугольника
Площадь многоугольника – это величина той части плоскости, которую занимает
многоугольник.
1 см
1 см
Слайд 8
2. ЕСЛИ МНОГОУГОЛЬНИК СОСТАВЛЕН ИЗ НЕСКОЛЬКИХ МНОГОУГОЛЬНИКОВ, ТО ЕГО ПЛОЩАДЬ РАВНА
СУММЕ ПЛОЩАДЕЙ ЭТИХ МНОГОУГОЛЬНИКОВ
Слайд 11
Теорема
Площадь прямоугольника равна произведению его смежных сторон
Площадь прямоугольника
S
b
a
Слайд 12
a
a
a
a
b
b
b
b
a2
b2
S
S
Дано:
ABCD-прямоугольник, AB=b, AD=a, SABCD=S
Доказать: S=ab
А
В
С
D
Доказательство:
1) Достроим прямоугольник до квадрата со стороной (a+b)
2) По свойству 3 Sкв. = (a+b)2
3) По свойству 2 имеем
SКВ =S + S + a2 + b2
S = ab
4) По свойству 1 имеем:
(a+b)2 = S + S + a2 + b2
а2 + 2ab + b2 = 2S + a2 + b2
2S = 2ab
Задачи
Слайд 14Площадь параллелограмма
Теорема
Площадь параллелограмма равна произведению его основания на высоту
А
B
C
D
Слайд 15
А
B
C
D
1
2
K
H
Дано: ABCD-параллелограмм
Доказать: S=AD · BH
Доказательство:
1. Трапеция
ABCK составлена из параллелограмма и треугольника DCK. С другой стороны, она составлена из прямоугольника HBCK и треугольника ABH.
2. Прямоугольные треугольники DCK и ABH равны (по гипотенузе и острому углу), поэтому их площади равны =>
3.Площади ABCD и HBCK также равны,т.е. площадь прямоугольника HBCK равна S.
По теореме => S=BC·BH,а так как BC=AD,то S=AD · BH
2. Прямоугольные треугольники DCK и ABH равны (по гипотенузе и острому углу), поэтому их площади равны =>
3.Площади ABCD и HBCK также равны,т.е. площадь прямоугольника HBCK равна S.
По теореме => S=BC·BH,а так как BC=AD,то S=AD · BH
Задачи
Слайд 16Площадь треугольника
Теорема
Площадь треугольника равна половине произведения его основания на высоту
А
В
С
Н
Слайд 17
А
В
С
D
.
Дано: АВС-треугольник, S-площадь
Доказать:
Доказательство:
1. Достроим
треугольник ACB до
параллелограмма ABDC.
2. Треугольники ABC и DCB равны
по трём сторонам =>площадь
треугольника АВС равна
половине площади параллелограмма
BDC, т.е.
параллелограмма ABDC.
2. Треугольники ABC и DCB равны
по трём сторонам =>площадь
треугольника АВС равна
половине площади параллелограмма
BDC, т.е.
Н
Слайд 18
2005
2006
207
2008
Если высоты двух треугольников равны, то их площади относятся как основания
Следствие
2
Площадь прямоугольного треугольника равна половине произведения его катетов
Следствие 1
Задачи
Слайд 19Площадь трапеции
Теорема
Площадь трапеции равна произведению полусуммы ее оснований на высоту
А
B
C
D
H
H1
Задачи
Слайд 55Дополнительные задания
Найдите периметр прямоугольника, если его площадь равна 72, а отношение
соседних сторон равно 1 : 2
36
30
42
24
24
Задание 1
Слайд 56
Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 8
и 18
Задание 2
12
14
16
10
Слайд 57
Задание 3
Даны два квадрата, диагонали которых равны 5 и 3. Найдите
диагональ квадрата, площадь которого равна разности площадей данных квадратов
Ответ: 4
Слайд 58
Стороны параллелограмма равны 15 и 9. Высота, опущенная на первую сторону,
равна 6. Найдите высоту, опущенную на вторую сторону параллелограмма
Площадь параллелограмма равна 40, стороны - 5 и 10. Найдите меньшую высоту этого параллелограмма
Найдите площадь параллелограмма, если его стороны равны 4 и 5, а угол между ними равен 30°
Задание 4
Задание 5
Задание 6
Ответ: 10
Ответ: 4
Ответ: 10
Слайд 59
Найдите площадь треугольника, две стороны которого равны 4 и 6, а
угол между ними равен 30°
Задание 7
20
10
6
8
Слайд 60
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую
сторону треугольника, если его площадь равна 100
Задание 8
Основания трапеции равны 10 и 35, площадь равна 225. Найдите ее высоту
Задание 9
Ответ:20
Ответ:10
Высота трапеции равна 20, площадь - 400. Найдите среднюю линию трапеции
Задание 10
Ответ:20
Слайд 61
Стороны прямоугольника 3 и 1. Найдите площадь четырехугольника, ограниченного биссектрисами углов
этого прямоугольника
Задание 10
Ответ: 2
