- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад НОУ по геометрии Формула Герона
Содержание
- 1. Презентация НОУ по геометрии Формула Герона
- 2. Актуальность проблемы Одной из самых интересных тем
- 3. Цель работы: доказать значимость и актуальность
- 4. ИСТОРИЧЕСКИЙ ЭКСКУРСГерон жил в Египте
- 5. Знаменитая формула Геронар - полупериметраbc
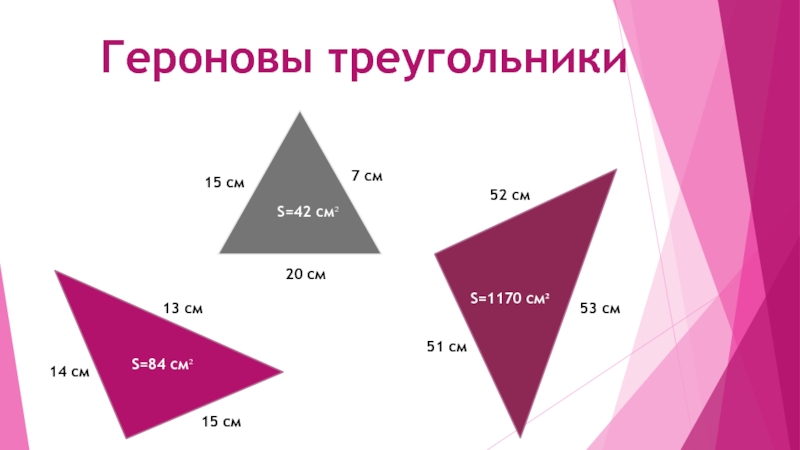
- 6. Героновы треугольники13 см15 см14 смS=84 см²7 см15 см20 см51 см52 см53 смS=42 см²S=1170 см²
- 7. Вывод формулы Герона:
- 8. Вывод формулы Герона:Следовательно,Но ,
- 9. Модифицированная формула ГеронаилиГипотеза: можно ли преобразовать формулу
- 10. ИССЛЕДОВАНИЕ ТРЕУГОЛЬНИКОВПусть треугольник прямоугольный с гипотенузой c
- 11. ПРАКТИЧЕСКАЯ ЧАСТЬ Задача 1. Стороны ∆AВC равны
- 12. Второй способ.Проведем высоту AD. Обозначим BD = x. Поскольку BC - наибольшая сторона треугольника, точка D лежит
- 13. Третий способ.Применим модифицированную формулу Герона:Ответ: 3√3..
- 14. Вывод: Наш опыт доказал, что мы можем
- 15. Задача 4. Диагонали трапеции равны 12 и
- 16. Задача 6.Стороны треугольника равны 13, 14 и
- 17. ЗАКЛЮЧЕНИЕОсновная цель данной работы - «реабилитировать»
Слайд 1Научное общество учащихся
Формула Герона
Выполнила: Кузнецова Кристина
МБОУ «Школа №66»
Руководитель: Китаева М.В.
учитель математики
Слайд 2Актуальность проблемы
Одной из самых интересных тем в курсе геометрии 8
Но, к сожалению, в школьном учебнике ей уделено недостаточно внимания.
В данной работе более подробно рассматривается формула Герона и ее применение, поскольку она значительно упрощает процесс решения задач, что важно как на контрольной работе, так и во время экзаменов.
Слайд 3Цель работы: доказать значимость и актуальность использования формулы Герона при решении
Задачи:
найти информацию о Героне Александрийском;
найти различные преобразования формулы Герона, позволяющие упростить громоздкость вычислений;
подобрать и решить задачи, применяя различные варианты формулы Герона;
сделать выводы из результатов исследования.
Слайд 4 ИСТОРИЧЕСКИЙ ЭКСКУРС
Герон жил в Египте в городе Александрия и
Наиболее известна "Метрика" Герона — научный труд, в котором приводится знаменитая формула Герона для определения площади треугольника по трем сторонам.
Герон Александрийский
Слайд 7 Вывод формулы Герона:
Пусть S — площадь
Доказать, что Доказательство:
Рассмотрим треугольник АВС, в котором АВ = с, ВС = а, АС = b.
Пусть А и В – острые углы треугольника АВС,
тогда основание Н высоты СН треугольника лежит на стороне АВ.
Введём обозначения СН= h, АН= y, HB=x.
По теореме Пифагора из ACH : h2 =b2-x2 и BCH: h 2 =a2-y2 , откуда
Так как , то
Сложив два последних равенства и разделив на 2, получим:
.
x
y
Слайд 9Модифицированная формула Герона
или
Гипотеза: можно ли преобразовать формулу Герона таким образом, чтобы
Слайд 10ИССЛЕДОВАНИЕ ТРЕУГОЛЬНИКОВ
Пусть треугольник прямоугольный с гипотенузой c и катетами a и
Тогда справедлива теорема Пифагора .
Подставляя полученное выражение в формулу ,
имеем: формула для вычисления площади прямоугольного
треугольника через длины его катетов.
Если треугольник равнобедренный с основанием a и боковой стороной b,
то
Если треугольник равносторонний со стороной a ,
то из равенства , получаем .
Если не выполнено неравенство треугольника, то и все подкоренное выражение
отрицательно. К примеру, если (не выполнено неравенство
треугольника), то и треугольник не существует.
Слайд 11ПРАКТИЧЕСКАЯ ЧАСТЬ
Задача 1.
Стороны ∆AВC равны 3, 4 и √13. Найдите
Решение: Пусть AB=3, AC= √13, BC=4
Первый способ.
По теореме косинусов АВ2 = АС2 + ВС2 – 2АС · ВС · соsC, отсюда
Т. к. sin2C + cos2C = 1, то
S∆AВC =
A
B D C
Слайд 12Второй способ.
Проведем высоту AD.
Обозначим BD = x.
Поскольку BC - наибольшая сторона треугольника,
точка D лежит на отрезке BC, поэтому CD = 4 − x.
По теореме
AD2=AB2 –BD2= 9 − x 2, AD2=AС2 –СD2= 13 − (4 − x) 2,
получим уравнение
9 − x 2 = 13 − (4 − x) 2
9 – x2 =13-16+8x- x2
x=1,5
BD = x=1,5.
Следовательно, AD 2 = AB 2 − BD 2 = 9-2,25=6,75;
A
B D C
Слайд 14Вывод: Наш опыт доказал, что мы можем обойтись в решении задачи
Итак, площадь треугольника по трем сторонам можно найти:
1)
сначала по теореме косинусов найти косинус какого – либо угла треугольника;
затем найти синус этого угла , а потом уже вычислить площадь треугольника по формуле
2)
выразить общий катет двух треугольников через одну переменную;
затем решить уравнение;
найти из прямоугольного треугольника высоту;
вычислить площадь по формуле
3) Применить формулу Герона.
Слайд 15Задача 4.
Диагонали трапеции равны 12 и 6, а сумма оснований
Решение:
Пусть
- диагонали трапеции
,
- её основания, причём
.
Через вершину C проведём прямую,
Пусть
– точка пересечения этой прямой с прямой
Тогда
- параллелограмм,
,
Если
- высота трапеции, то
.
По формуле Герона
параллельную диагонали
Ответ:
Слайд 16Задача 6.
Стороны треугольника равны 13, 14 и 15. Найдите радиус окружности,
Решение:
Пусть AC = 13, AB = 14, BC = 15, O — центр указанной окружности (O на стороне AB), R — её радиус, P и Q — точки касания окружности со сторонами AC и BC соответственно.
По формуле Герона
SABC =
=
= 84.
Поскольку OP и OQ — высоты треугольников AOC и BOC, то
SABC = SAOC + SBOC =
AC . OP +
BC . OQ =
(AC + BC)R = 14R.
Следовательно, R =
=
= 6.
Ответ: 6.
Слайд 17 ЗАКЛЮЧЕНИЕ
Основная цель данной работы - «реабилитировать» и актуализировать формулу Герона
Для этого были рассмотрены задачи разного уровня сложности, в решении которых использовалась формула Герона, и ее модификация.
Получив модифицированную формулу, я не могла не оценить её преимущества:
во-первых, она дает значительный выигрыш во времени;
во-вторых, существенно облегчает вычисления при решении задач, что особенно важно, т.к. большинство учеников отказывается от использования данной формулы, когда даны иррациональные числа;
в-третьих, я сделала для себя удивительное открытие. Оказывается, что все формулы для вычисления площади треугольника, связаны с формулой Герона.
Считаю цель достигнутой, необходимость более детального изучения данной формулы актуально, так как умение вычислять площадь геометрических фигур нужно не только в школе для решения задач, но и в повседневной жизни.