- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад материалов к уроку геометрии в 11 классе Объём шара
Содержание
- 1. Презентация материалов к уроку геометрии в 11 классе Объём шара
- 2. Объём шараОбщая формула для объёмов тел вращения:
- 3. Объём шараВывод формулы вычисления объёма шара:
- 4. ШАРОВОЙ СЕГМЕНТОпределение:Шаровой сегмент – это часть шара, отсекаемая от него плоскостью
- 5. ОБЪЁМ ШАРОВОГО СЕГМЕНТА
- 6. ШАРОВОЙ СЕКТОРОпределение:Шаровой сектор – это тело, которое
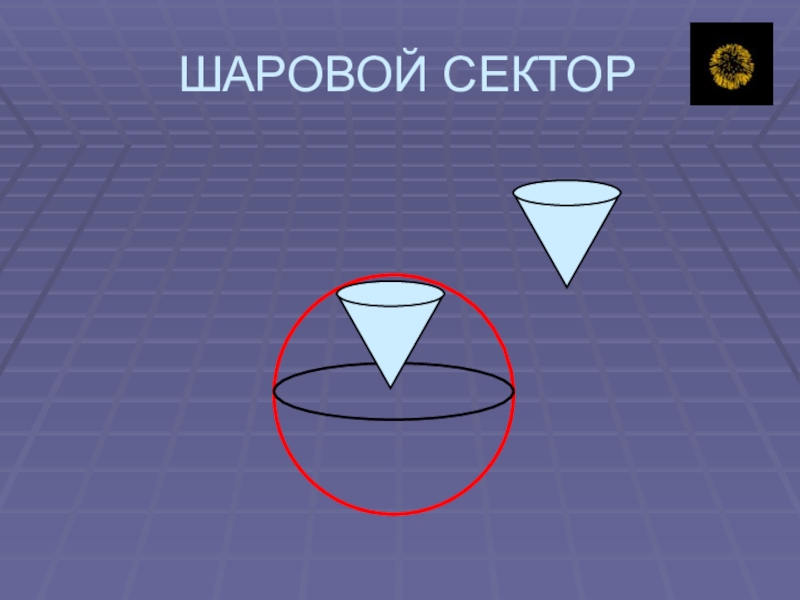
- 7. ШАРОВОЙ СЕКТОР
- 8. ОБЪЁМ ШАРОВОГО СЕКТОРАV = 2/3 π R2 H
Объём шараОбщая формула для объёмов тел вращения: aV = ∫ π f 2(x) dx
Слайд 3Объём шара
Вывод формулы вычисления объёма шара:
y A(-R; 0), B(R;0) х2 +у2 = R2
Полуокружность, расположенная над
‘ осью х задаётся уравнением
у = f(x)=√R2 - х2 , -R< x ≤R
b R R
A B V = ∫ π f 2(x) dx= ∫ π f 2(x) dx= π ∫(R2 - х2) dx=
x a -R -R
= π (R2х –x3/3) R =4/3 π R3
-R
Полуокружность, расположенная над
‘ осью х задаётся уравнением
у = f(x)=√R2 - х2 , -R< x ≤R
b R R
A B V = ∫ π f 2(x) dx= ∫ π f 2(x) dx= π ∫(R2 - х2) dx=
x a -R -R
= π (R2х –x3/3) R =4/3 π R3
-R
Слайд 5ОБЪЁМ ШАРОВОГО СЕГМЕНТА
b R R
V = ∫ π f 2(x) dx= ∫ π f 2(x) dx= π ∫(R2 – х2) dx=
a R-Н R-Н
= π (R2х –x3/3) R = πH2 (R – H/3)
R-Н
Слайд 6ШАРОВОЙ СЕКТОР
Определение:
Шаровой сектор – это тело, которое получается из шарового сегмента
и конуса.
Причём, если шаровой сегмент меньше полушара, то он дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. А если сегмент больше полушара, то указанный конус из него удаляется.
Причём, если шаровой сегмент меньше полушара, то он дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. А если сегмент больше полушара, то указанный конус из него удаляется.