- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад математика Квадрат теңдеу түбірлерінің формулалары 8 класс
Содержание
- 1. Презентация математика Квадрат теңдеу түбірлерінің формулалары 8 класс
- 2. Слайд 2
- 3. ax2 + bx + c = 0 теңдеуін коэффициенттерінің қасиеттері
- 4. «Ой қозғау»Толымды квадрат теңдеу:ах2 + bx +
- 5. - квадрат теңдеудің дискриминанты
- 6. Берілген теңдеулердің арасынан толық және толымсыз квадрат
- 7. Кестені толтыр!
- 8. Теңдеулерді шешіңдер:Теңдеулерді шешіңдер:
- 9. Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін,
- 10. Бұл мысалдардан, келтірілген квадраттық теңдеу түбірлерінің
- 11. Түбірлері
- 12. Тест тапсырмалары
- 13. Слайд 13
- 14. Жауаптарыңызды тексеріңіздер: 1-нұсқа
- 15. Слайд 15
Бар ізгілік тек білімнен алынар,
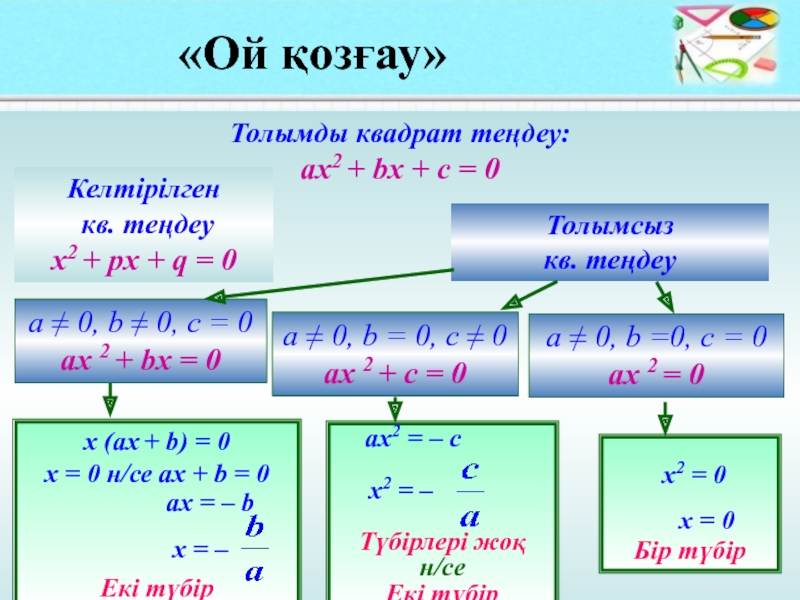
Слайд 4«Ой қозғау»
Толымды квадрат теңдеу:
ах2 + bx + c = 0
Келтірілген
кв. теңдеу
х2 + px + q = 0
Толымсыз
кв. теңдеу
a ≠ 0, b ≠ 0, c = 0
ах 2 + bx = 0
a ≠ 0, b = 0, c ≠ 0
ах 2 + c = 0
a ≠ 0, b =0, c = 0
ах 2 = 0
x (ах + b) = 0
х = 0 н/се ах + b = 0
ах = – b
x = –
Екі түбір
ах2 = – c
x2 = –
Түбірлері жоқ
н/се
Екі түбір
х2 = 0
x = 0
Бір түбір
Слайд 5- квадрат теңдеудің дискриминанты
3 жағдай болуы мүмкін:
- түбірлері жоқ
- бір түбір
- екі түбір
Слайд 6Берілген теңдеулердің арасынан толық және толымсыз квадрат теңдеулерді атаңдар
а) х2
+ 3х – 19 =0, б) х2-7х+11=0,
ә) 4х2+5х=0, д) 2х2-5х+1=0,
в) 8х2=0, г) 3х2-21х=0.
ғ) 8х2-3х=0, е) х2-25=0,
ж) х2-4х=45 з) 18-2х2=0
и) 4х2-28х+49=0 к) 2х2-5х+3=0
ә) 4х2+5х=0, д) 2х2-5х+1=0,
в) 8х2=0, г) 3х2-21х=0.
ғ) 8х2-3х=0, е) х2-25=0,
ж) х2-4х=45 з) 18-2х2=0
и) 4х2-28х+49=0 к) 2х2-5х+3=0
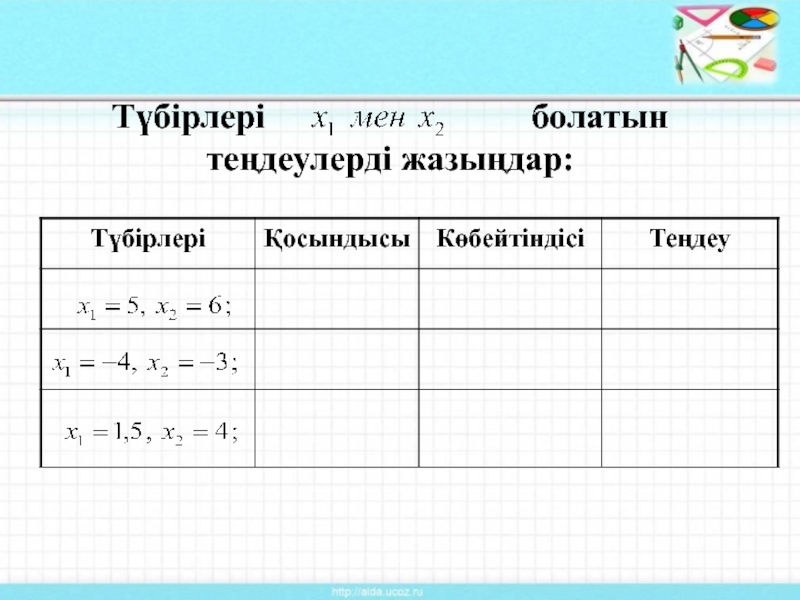
Слайд 9Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін, түбірлерінің қосындысы мен көбейтіндісінің
мәндерін табыңдар және жауаптарын кестеге толтырыңдар.
Слайд 10 Бұл мысалдардан, келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған
екінші коэффициентке, ал көбейтіндісі бос мүшеге тең екенін байқадық.
Енді бұл қасиетті теорема ретінде тұжырымдап шығайық.
Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады:
Енді бұл қасиетті теорема ретінде тұжырымдап шығайық.
Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады: