МБОУ “Сош №1 г. Калининска”
Довыденков Иван
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Квадратура круга по геометрии
Содержание
- 1. Презентация Квадратура круга по геометрии
- 2. “Квадратура круга”. Условие. Кратко говоря, квадратура –
- 3. ИсторияЗадача берёт своё начало в Древней Греции.
- 4. Попытки решитьГиппократ Хиосский в IV веке до н.
- 5. Попытки решить
- 6. Попытки решитьДальнейшие исследования индийских, исламских и европейских математиков по этой
- 7. Решение
- 8. РешениеОднако, задача имеет решение, если прибегнуть к механике. Во-первых, квадратриса, которая представляет собой кривую, вычисляемую кинематически.
- 9. Решение
- 10. РешениеТакже было выведено приближённое решение. Согласно ему,
- 11. Метафора “Квадратура круга”Математическое доказательство невозможности квадратуры круга
- 12. Конец
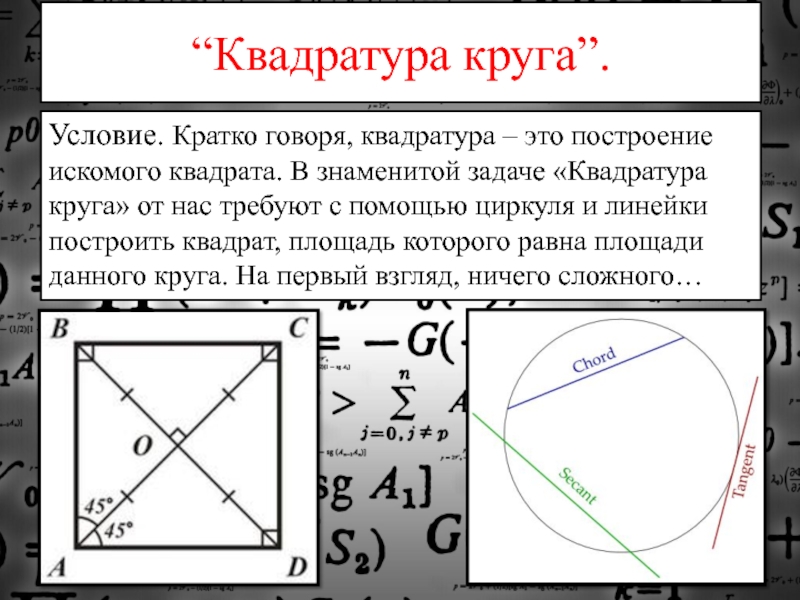
“Квадратура круга”. Условие. Кратко говоря, квадратура – это построение искомого квадрата. В знаменитой задаче «Квадратура круга» от нас требуют с помощью циркуля и линейки построить квадрат, площадь которого равна площади данного круга. На первый взгляд, ничего
Слайд 1“Квадратура круга”
Презентация на конкурс: “Красивая задача”
Презентацию подготовил ученик 10 б класса
Слайд 2“Квадратура круга”.
Условие. Кратко говоря, квадратура – это построение искомого квадрата.
В знаменитой задаче «Квадратура круга» от нас требуют с помощью циркуля и линейки построить квадрат, площадь которого равна площади данного круга. На первый взгляд, ничего сложного…
Слайд 3История
Задача берёт своё начало в Древней Греции. Древнегреческие математики считали своей
задачей не вычисление, а точное построение искомого квадрата причём, в соответствии с тогдашними принципами, только с помощью циркуля и линейки. Проблемой занимались крупнейшие античные учёные — Анаксагор, Антифон, Архимед и другие.
Слайд 4Попытки решить
Гиппократ Хиосский в IV веке до н. э. первым обнаружил, что
некоторые криволинейные фигуры (гиппократовы луночки) допускают точную квадратуру. Расширить класс таких фигур античным математикам не удалось. По другому пути пошёл его современник Динострат, показавший, что квадратуру круга можно строго выполнить с помощью особой кривой — квадратрисы. Но, этот метод относится к области механики, а условие требует применения лишь циркуля и линейки.
Слайд 6Попытки решить
Дальнейшие исследования индийских, исламских и европейских математиков по этой теме долгое время касались
в основном уточнения значения числа π и подбора приближённых формул для квадратуры круга. В средневековой Европе задачей занимались Фибоначчи, Николай Кузанский и Леонардо да Винчи. Позднее обширные исследования опубликовали Кеплер и Гюйгенс.
Слайд 8Решение
Однако, задача имеет решение, если прибегнуть к механике. Во-первых, квадратриса, которая
представляет собой кривую, вычисляемую кинематически.
Слайд 10Решение
Также было выведено приближённое решение. Согласно ему, диагональ искомого квадрата примерно
равна 2,5 радиусам круга. После этого допущения задача становится вполне выполнимой.
Слайд 11Метафора “Квадратура круга”
Математическое доказательство невозможности квадратуры круга не мешало многим энтузиастам
тратить годы на решение этой проблемы. Тщетность исследований по решению задачи перенесла этот оборот во многие другие области, где он попросту обозначает безнадежное или бессмысленное предприятие.