- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Кривые второго порядка
Содержание
- 1. Презентация Кривые второго порядка
- 2. Кривые второго порядкаЭллипсГиперболаПараболаВыход
- 3. ЭллипсОсновные понятияПримерГрафикГлавное меню
- 4. ЭллипсЭллипсом называется множество всех точек плоскости, сумма
- 5. Далее, обозначим через r1 и r2 расстояния
- 6. Если оси координат расположены по отношению к
- 7. НазадИ находится по формуле: Форма эллипса
- 8. Пример 1. Составить каноническое уравнение эллипса, проходящего
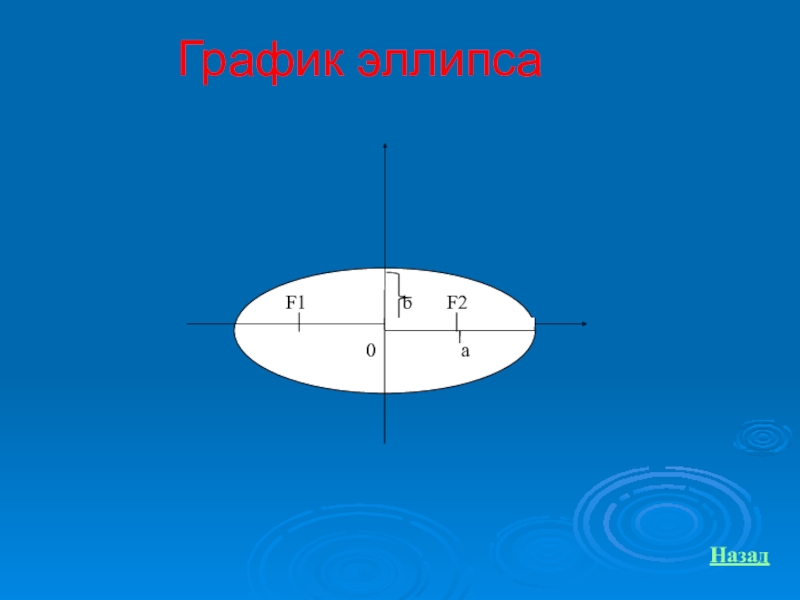
- 9. График эллипсаНазад
- 10. ПараболаОсновные понятияПримерГрафикГлавное меню
- 11. ПараболаПараболой называется множество всех точек плоскости, каждая
- 12. Точка O называется вершиной параболы, ось
- 13. Пример 1:Дано уравнение параболы Решение:Сравнивая данное уравнение
- 14. Слайд 14
- 15. ГиперболаОсновные понятияПримерГрафикГлавное меню
- 16. ГиперболаГиперболой называется множество всех точек плоскости, для
- 17. Оси симметрии называются осями гиперболы, а центр
- 18. НазадЕсли за оси координат принять асимптоты
- 19. Пример:Дано уравнение гиперболы полуоси, координаты фокусов, эксцентриситет;
- 20. График гиперболыYXB’BbC’CF1F2A’Aa0Назад
Слайд 4Эллипс
Эллипсом называется множество всех точек плоскости, сумма расстояний от которых до
Обозначим фокусы эллипса через F1 и F2. Пусть M – произвольная точка эллипса. Расстояние |F1 F2| между фокусами обозначим 2c, сумму расстояний от точки M до фокусов – через 2a. Так как по определению эллипса |F1M| +|F2M|> |F1 F2|, то 2a>2с или a>c.
Далее
Слайд 5Далее, обозначим через r1 и r2 расстояния от точки М
до
Числа r 1 и r2 называются фокальными радиусами точки М.
Следовательно точка М(x; y) принадлежит данному эллипсу
тогда и только тогда, когда r1+r2=2a.
Далее
Слайд 6Если оси координат расположены по отношению к эллипсу таким образом, что
Таким образом, эллипс – линия второго порядка. Оси
симметрии эллипса называются его осями, а центр симметрии
(точка пересечения осей) – центром эллипса. Точки,
в которых эллипс пересекает оси, называются его вершинами.
Так как на а>=b, то 2а – длина большой оси
симметрии эллипса, 2b – малой оси.
.
.
Далее
Где a – длина большой полуоси, b – длина малой полуоси и они
связаны соотношением
Слайд 7
Назад
И находится по формуле:
Форма эллипса (степень его сжатия) зависит
соотношения между а и с (половина расстояния между
фокусами) называется эксцентриситет.
Слайд 8
Пример 1. Составить каноническое уравнение эллипса, проходящего
через точки М1(2; 3)
Решение: Пусть искомое уравнение эллипса имеет вид
точек удовлетворяют этому уравнению. Подставив вместо x и y сначала координаты
точки М1, а затем координаты точки М2, получим систему уравнений
Пусть
получаем
решив которую находим
откуда а2=16, b2=12. Следовательно, искомое уравнение имеет вид:
).
. Координаты данных
Назад
Составить каноническое уравнение эллипса, проходящего через точки М
и N
Решение:
Пример 2.
Пусть
Искомое уравнение эллипса. Этому уравнению должны
удовлетворять координаты данных точек.
Следовательно,
Отсюда находим
Уравнение эллипса имеет вид
Слайд 11Парабола
Параболой называется множество всех точек плоскости, каждая из которых находиться на
Далее
Если директриса параболы оси y и находится на равном
расстоянии от начала координат с фокусом, то уравнение
Параболы имеет вид:
-симметрична оси Y .
Слайд 12
Точка O называется вершиной параболы, ось симметрии (ось Оx) –
Число p, т. е. параметр параболы выражает расстояние от фокуса до директрисы.
Параметр параболы влияет на её форму.
Назад
Слайд 13Пример 1:
Дано уравнение параболы
Решение:
Сравнивая данное уравнение с каноническим уравнением параболы
получаем, что 2p=6, откуда p=3. Так как фокус параболы имеет координаты
а директриса – уравнение
, то для данной параболы получаем:
и уравнение директрисы
.
. Составить уравнение её директрисы и найти
координаты её фокуса.
,
,
координаты фокуса
Назад
Пример 2.
Составить уравнение параболы с вершиной в начале координат, симметричной
относительно оси Oy и отсекающей на биссектрисе 1 и 3 координатных углов хорду
длиной
Искомое уравнение параболы
уравнение биссектрисы y=x.
Получаем точки пересечения параболы с биссектрисой: О(0;0) и М(2p; 2p).
Решение:
Длина хорды
, откуда 2p=8. Искомое уравнение
Слайд 16Гипербола
Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний
.
.
Далее
Если гипербола расположена таким образом, что её фокусы
Находятся на оси x на равном расстоянии от начала
Координат , то она задаётся каноническим уравнением
Слайд 17
Оси симметрии называются осями гиперболы, а центр симметрии(точка пересечения осей) –
которые называются её вершинами. Одна ось называется действительной осью,
а другая ось не имеет общих точек с гиперболой и называется мнимой осью
гиперболы. Прямоугольник BB’C’C со сторонами 2а и 2b называется основным прямоугольником гиперболы. Величины a и b называются соответственно
действительной и мнимой полуосями гиперболы
.
Гипербола с равными полуосями (а=b) называется
равносторонней,
,
фокусами, а – большая полуось гиперболы.
Далее
Слайд 18
Назад
Если за оси координат принять асимптоты равносторонней
гиперболы, то её
пропорциональности.
Две гиперболы:
имеют одни и те же асимптоты, но действительная
называются сопряженными.
ось одной служит мнимой осью
другой такие гиперболы
Слайд 19Пример:
Дано уравнение гиперболы
полуоси, координаты фокусов, эксцентриситет; составить уравнение её асимптот.
Решение:
Приведём
что действительная полуось а=2, а мнимая полуось
гиперболы имеют уравнения
эксцентриситет ε=
, а
координаты фокусов
и
; эксцентриситет ε=
и уравнение асимптот
. Найти её действительную и мнимую
, находим,
. Так как асимптоты
, фокусы – координаты (-с; 0) и (с; 0)
, то для данной гиперболы получаем:
Назад