Презентация, доклад Конус и его элементы.

Содержание

1. Презентация Конус и его элементы.
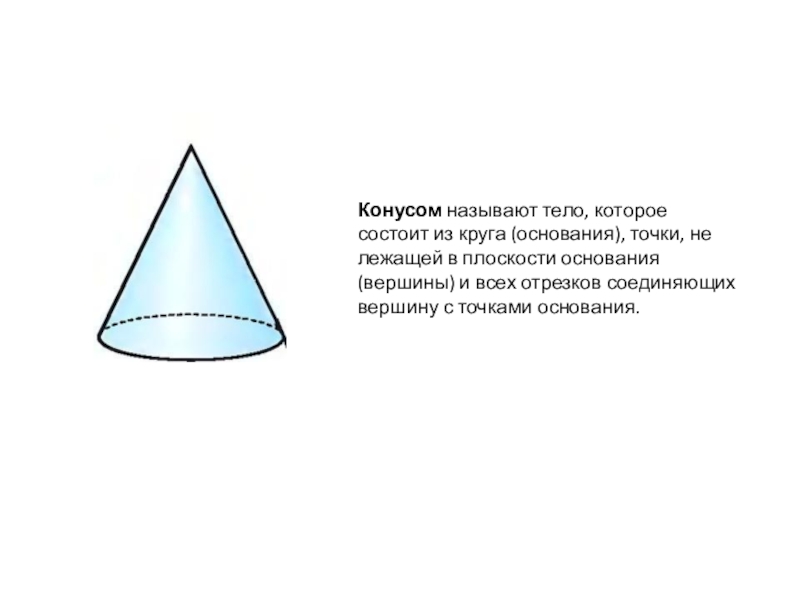
2. Конусом называют тело, которое состоит из круга
3. Слайд 3
4. Отрезки, соединяющие вершину конуса с точками окружности
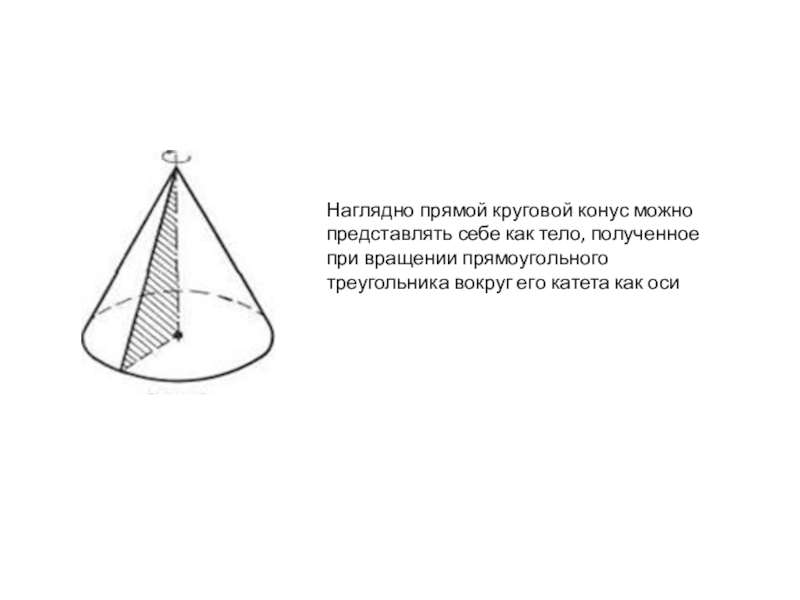
5. Наглядно прямой круговой конус можно представлять себе
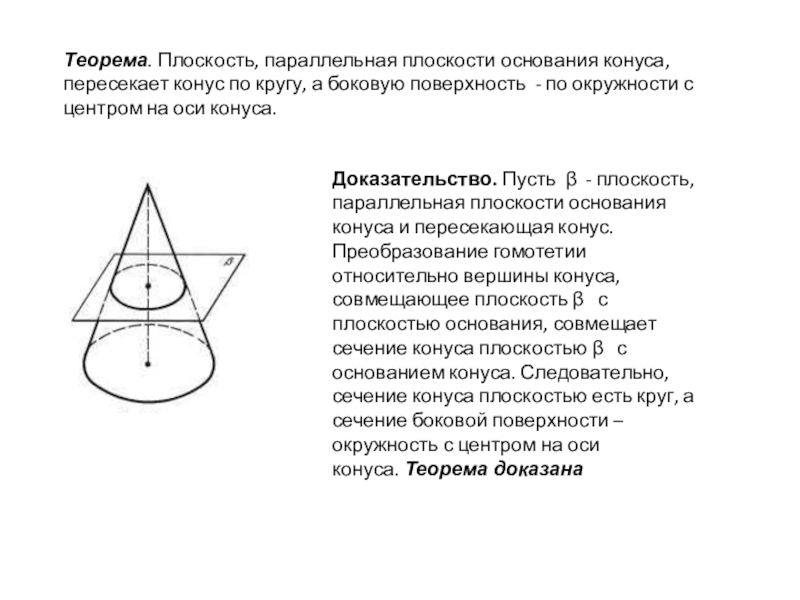
6. Теорема. Плоскость, параллельная плоскости основания конуса, пересекает
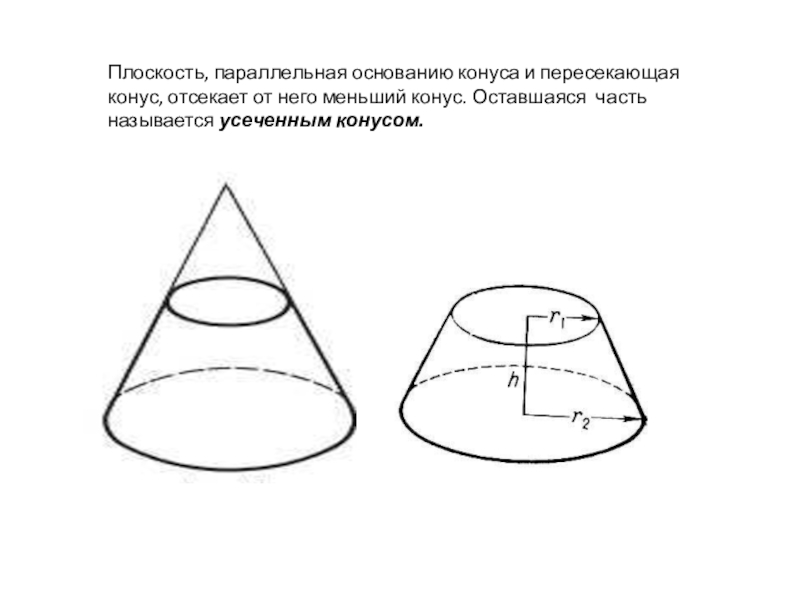
7. Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.
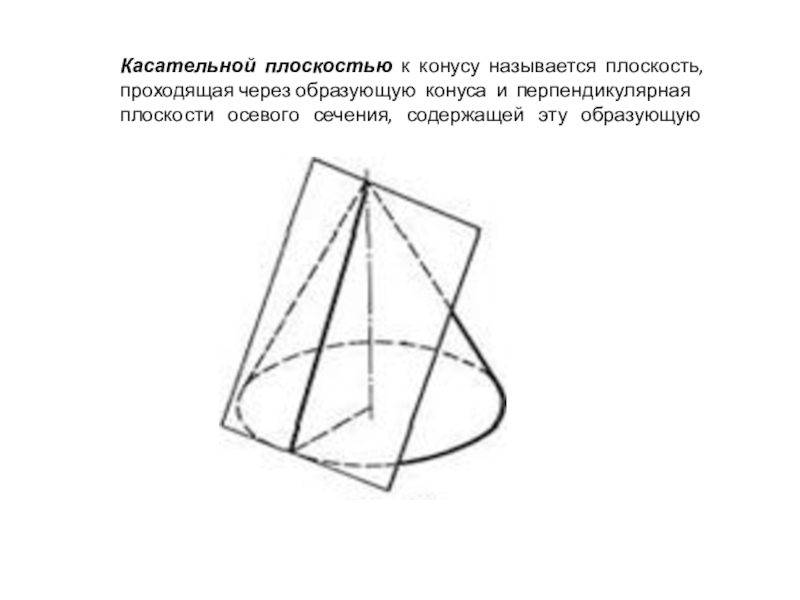
8. Касательной плоскостью к конусу называется плоскость, проходящая через
9. Площадь боковой поверхности конуса:S=π⋅R⋅l, где R — радиус основания
10. Конусы вокруг нас.

Конусом называют тело, которое состоит из круга (основания), точки, не лежащей в плоскости основания (вершины) и всех отрезков соединяющих вершину с точками основания.

Главная
Геометрия
Презентация Конус и его элементы.

Слайд 1Конус и его элементы

Слайд 2Конусом называют тело, которое состоит из круга (основания), точки, не лежащей

в плоскости основания (вершины) и всех отрезков соединяющих вершину с точками основания.

Конусом называют тело, которое состоит из круга (основания), точки, не лежащей в плоскости основания (вершины) и всех

Слайд 3

Слайд 4Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса.
Конус называется прямым,

если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания.

Осью прямого кругового конуса называется прямая, содержащая его высоту.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса.Конус называется прямым, если прямая, соединяющая вершину конуса с

Слайд 5Наглядно прямой круговой конус можно представлять себе как тело, полученное при

вращении прямоугольного треугольника вокруг его катета как оси

Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета

Слайд 6Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а

боковую поверхность - по окружности с центром на оси конуса.

Доказательство. Пусть β - плоскость, параллельная плоскости основания конуса и пересекающая конус. Преобразование гомотетии относительно вершины конуса, совмещающее плоскость β с плоскостью основания, совмещает сечение конуса плоскостью β с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности – окружность с центром на оси конуса. Теорема доказана

Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность - по окружности с

Слайд 7Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший

конус. Оставшаяся часть называется усеченным конусом.

Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.

Слайд 8Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная

плоскости осевого сечения, содержащей эту образующую

Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую

Слайд 9Площадь боковой поверхности конуса:

S=π⋅R⋅l,

где R — радиус основания конуса, l — длина образующей.
Площадь

боковой поверхности усеченного конуса:

S=π(r1+r2)⋅l

где r1, r2 — радиусы оснований конуса,
l — длина образующей

Площадь боковой поверхности конуса:S=π⋅R⋅l, где R — радиус основания конуса, l — длина образующей.Площадь боковой поверхности усеченного конуса:S=π(r1+r2)⋅l где r1,

Слайд 10Конусы вокруг нас.

Скачать презентацию

Презентация, доклад Конус и его элементы.

Содержание

Слайд 1Конус и его элементы

Слайд 2Конусом называют тело, которое состоит из круга (основания), точки, не лежащей

Слайд 3

Слайд 4Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса.
Конус называется прямым,

Слайд 5Наглядно прямой круговой конус можно представлять себе как тело, полученное при

Слайд 6Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а

Слайд 7Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший

Слайд 8Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная

Слайд 9Площадь боковой поверхности конуса:

S=π⋅R⋅l,

где R — радиус основания конуса, l — длина образующей.
Площадь

Слайд 10Конусы вокруг нас.

Что такое shareslide.ru?

Обратная связь

Презентация, доклад Конус и его элементы.

Содержание

Слайд 1Конус и его элементы

Слайд 2Конусом называют тело, которое состоит из круга (основания), точки, не лежащей

Слайд 3

Слайд 4Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса.Конус называется прямым,

Слайд 5Наглядно прямой круговой конус можно представлять себе как тело, полученное при

Слайд 6Теорема. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а

Слайд 7Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший

Слайд 8Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная

Слайд 9Площадь боковой поверхности конуса:S=π⋅R⋅l, где R — радиус основания конуса, l — длина образующей.Площадь

Слайд 10Конусы вокруг нас.

Похожие презентации

Что такое shareslide.ru?

Обратная связь

Слайд 4Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса.
Конус называется прямым,

Слайд 9Площадь боковой поверхности конуса:

S=π⋅R⋅l,

где R — радиус основания конуса, l — длина образующей.
Площадь