- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к выступлению на НПК Две теоремы косинусов для четырёхугольников
Содержание
- 1. Презентация к выступлению на НПК Две теоремы косинусов для четырёхугольников
- 2. » Муниципальное бюджетное общеобразовательное учреждение
- 3. Объект исследования: две теоремы косинусов для четырехугольника.
- 4. Теорема косинусов для четырехугольника №1 Квадрат стороны
- 5.
- 6. Слайд 6
- 7. Теорема косинусов для четырехугольника №2
- 8. Некоторые следствия из теоремы №2l2 f2 =
- 9. 3. Во всяком выпуклом четырехугольнике, вписанном
- 10. Спасибо за внимание!
Слайд 2» Муниципальное бюджетное общеобразовательное учреждение «Копьёвская средняя общеобразовательная школа с углублённым
Автор:
Давыдович Антон Юрьевич,
учащийся 10Б класса
Руководитель:
Загородних Ольга Иосифовна,
учитель математики
п. Копьёво, 2014 г.
Слайд 3
Объект исследования: две теоремы косинусов для четырехугольника.
Предмет исследования: метрические
Гипотеза: для четырехугольника существуют теоремы, которые по аналогии с соответствующими теоремами для треугольника, называются теоремами косинусов.
Цели исследования: изучение теорем о метрических соотношениях в четырехугольнике.
Задачи исследования: изучить два доказательства первой теоремы косинусов для четырёхугольника, формулировку второй и доказательства некоторых следствий из второй теоремы.
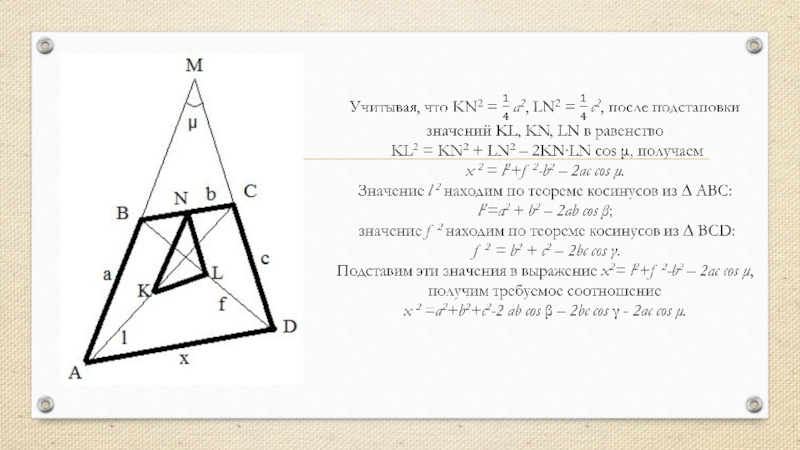
Слайд 4Теорема косинусов для четырехугольника №1 Квадрат стороны выпуклого четырехугольника равен сумме квадратов
Доказательство 1.
Слайд 7Теорема косинусов для четырехугольника №2
Квадрат произведения диагоналей простого четырехугольника равен сумме
l2 f2 = a2 c2 +b2 d2 - 2 abcd cos φ, где φ- угол, равный сумме углов A и C или B и D.
Вторая теорема косинусов (теорема Бретшнейдера, 1843 г.), редко встречается в русской и иностранной учебной литературе по элементарной геометрии.
Слайд 8Некоторые следствия из теоремы №2
l2 f2 = a2 c2 +b2 d2
1. Если сумма какой- либо пары противолежащих углов равна 90˚, то квадрат произведения диагоналей равен сумме квадратов произведений противолежащих сторон четырехугольника.
l2 f2 = a2 c2 +b2 d2.
2. В параллелограмме с острым углом, равным 45˚, квадрат произведения диагоналей равен сумме четверых степеней неравных сторон.
l2 f2 = a2 c2 +b2 d2,
при а = с и b = d l2 f2 = a4 + b4.
Слайд 9 3. Во всяком выпуклом четырехугольнике, вписанном в окружность, произведение диагоналей равно
Во вписанном четырехугольнике
сумма углов А и С равна 180˚,
значит, (l f)2 = (ac)2 + (bd)2 + 2abcd,
или (l f)2= (ac + bd)2,
то есть l f = ac + bd.
l2 f2 = a2 c2 +b2 d2 - 2 abcd cos φ.