- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к выступлению на конференцию по математике: Практическое применение подобия треугольников.
Содержание
- 1. Презентация к выступлению на конференцию по математике: Практическое применение подобия треугольников.
- 2. Цель работы: узнать больше о подобии треугольников, и
- 3. Треугольники знакомы нам с детства. Более
- 4. “Определение высоты предмета” С помощью тени (способ
- 5. За шесть веков до нашей эры греческий
- 6. В один прекрасный день Фалес нашёл длинную
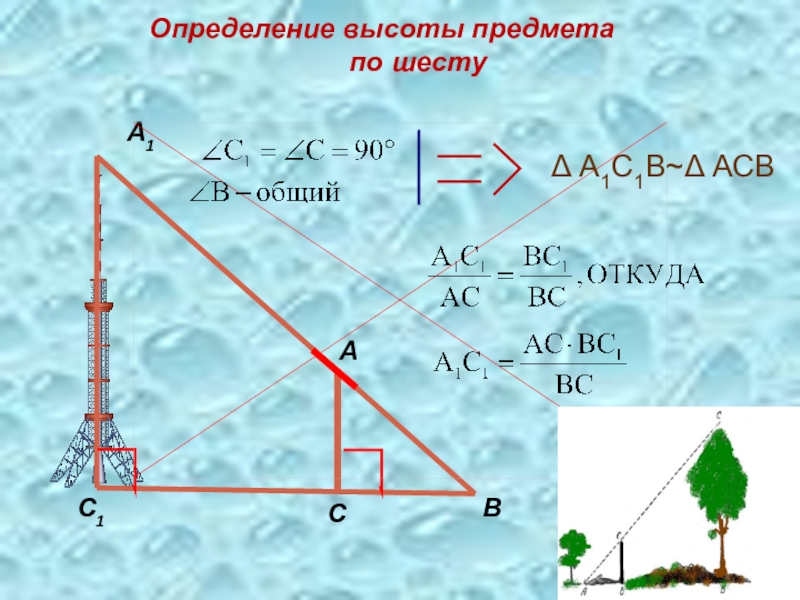
- 7. Определение высоты предмета
- 8. Способ Жюль Верна
- 9. Способ Жюль Верна
- 10. Слайд 10
- 11. Определение высоты предмета по лужеЭтот способ можно
- 12. Определение высоты предмета
- 13. Слайд 13
- 14. Слайд 14
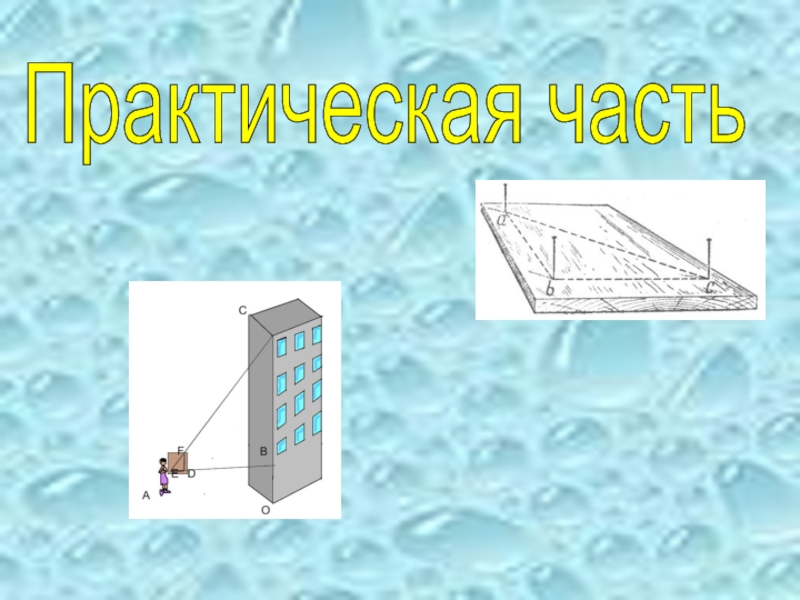
- 15. Практическая часть
- 16. Измерения с помощью булавочного прибора Мы взяли
- 17. Способ с монетойЧитая литературу, я познакомилась
- 18. Вывод: Подобие треугольников в жизни незаменимо. Подобие
- 19. Спасибо за внимание!
Слайд 1
Практическое
применение
подобия
треугольников
Выполнила: Кузнецова Татьяна, 8 класс
Муниципальное бюджетное
Слайд 2Цель работы:
узнать больше о подобии треугольников, и каким образом оно применяется
Применить на практике полученные знания.
Задачи:
Познакомиться с литературой по данному вопросу.
Изготовить необходимое оборудования для измерения на местности..
Показать умение проводить измерительные работы на местности
Слайд 3 Треугольники знакомы нам с детства. Более подробно мы узнали о
С помощью треугольника можно решать много практических задач. В жизни весьма важное значение имеют измерительные работы на местности, где применяется подобие треугольников.
Подобие треугольников можно применять для разных целей. Например, для измерения предмета.
Слайд 4“Определение высоты предмета”
С помощью тени (способ Фалеса);
При помощи шеста с вращающейся
С помощью зеркала;
С помощью равнобедренного прямоугольного треугольника;
При помощи монеты
При помощи записной книжки
Слайд 5За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил
Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час,
когда длина собственной его тени
равнялась его росту. В этот момент высота пирамиды
должна также равняться
длине отбрасываемой
его тени.
Вот, пожалуй, единственный
случай, когда человек
извлёк пользу из своей тени.
Способ Фалеса
Слайд 6В один прекрасный день Фалес нашёл длинную палку, воткнул её в
Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида.
СЕ=ED, т.е. H=b
Преимущества:
не требуются вычисления.
Недостатки:
нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.
D
C
E
H
b
Слайд 8Способ Жюль Верна
романе «Таинственный остров».
Там инженер и Герберт измеряют
высоту площадки дальнего вида.
Я же расскажу этот способ на
Примере измерения дерева.
Здесь нужен шест, который
придется воткнуть в землю
отвесно так, чтобы выступающая
часть как раз ровнялась
росту человека. Место
для шеста надо выбирать так,
чтобы лежа было видно
верхушку дерева на одной прямой
линии с верхней точкой шеста. Получим два прямоугольных треугольника. Катетами первого будет являться шест и расстояние от шеста до головы человека лежащего на земле. Катетами второго треугольника будут являться: расстояние от головы человека до дерева и та высота дерева, которую нам нужно определить. Мы можем определить расстояние от головы до шеста и от головы до дерева, так же нам известна высота шеста, следовательно, мы можем составить пропорцию и найти искомую высоту.
Слайд 10
можно производить измерения в любую
погоду;
простота формулы.
Недостатки:
нельзя
измерить высоту
предмета не испачкавшись, так как приходится
ложиться на землю.
Способ Жюль Верна
Слайд 11Определение высоты предмета по луже
Этот способ можно удачно применять после дождя,
Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас
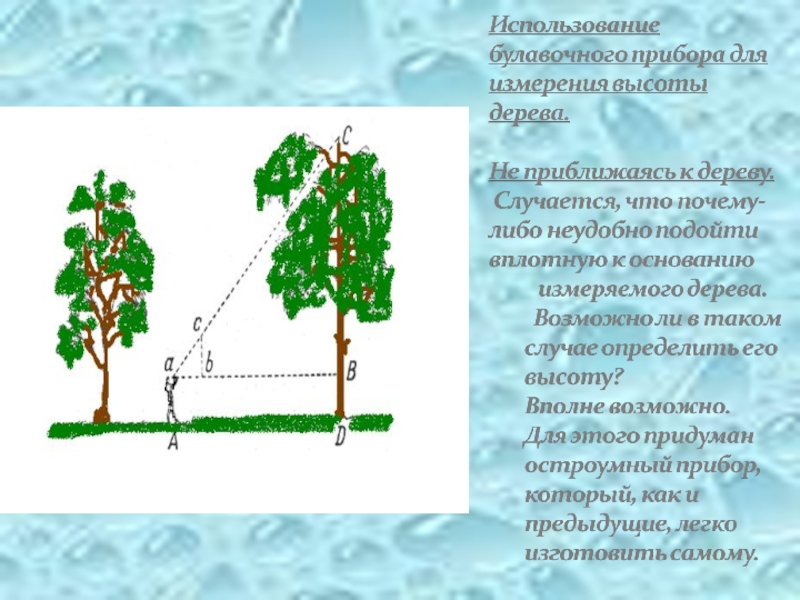
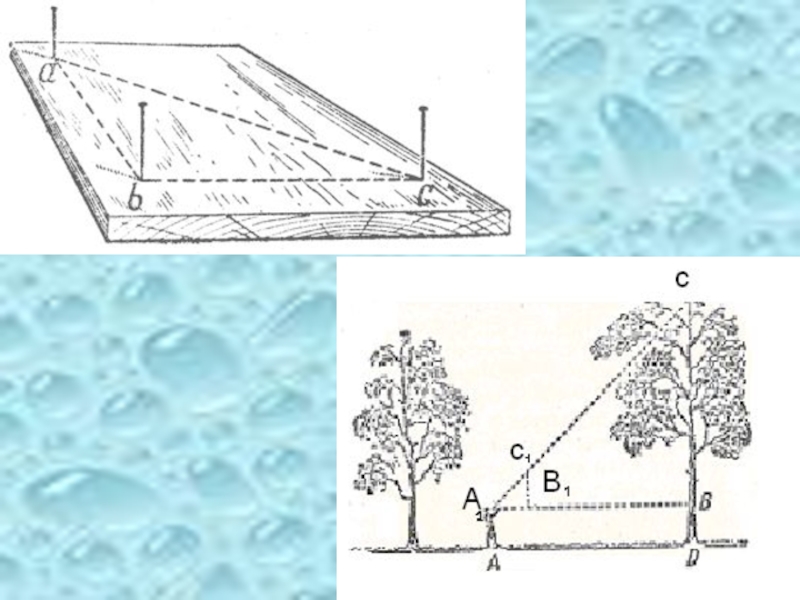
Слайд 16Измерения с помощью булавочного прибора
Мы взяли прибор, который сами изготовили
продолжением гипотенузы ЕF треугольника EFD.
Так как угол Е = 45 градусов,
то EFD равнобедренный,
а значит ЕСВ тоже равнобедренный.
Мы измерили расстояние ВЕ, оно получилось
равно 23 шага,
это 1150 см и прибавили к нему ОВ=160 см.
Высота школы
получилась равна 1310 см=13,1 м
Слайд 17 Способ с монетой
Читая литературу, я познакомилась вот с такой задачей:
Дерево
Решить ее довольно просто.
=> ﮮ НРК = ﮮ НАВ
=> ﮮ НМК = ﮮ НОВ
∆НАВ и ∆НРК
ﮮ НРК = ﮮ НАВ
=>
ﮮ НМК = ﮮ НОВ
∆НАВ подобен ∆НРК
КР : АВ = НМ : НО
2см : 1500см = 70см : НО
НО== 52500см = 525м
Ответ: 525м.
Слайд 18Вывод:
Подобие треугольников в жизни незаменимо. Подобие применяется от школьной тетради вплоть
Я узнала много нового о подобии и его применении. Знания, полученные в ходе исследовательской работы, останутся в моей памяти надолго.
Я исследовала различные способы измерения на местности и применила их на практике. Также изготовила прибор для этих измерений.