- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку:Правильные многогранники
Содержание
- 1. Презентация к уроку:Правильные многогранники
- 2. СодержаниеВведениеИстория появления многогранниковПравильный многогранник и его видыПравильные многогранники в природеПолуправильные многогранникиЗвездчатые многогранникиЗаключениеЛитература
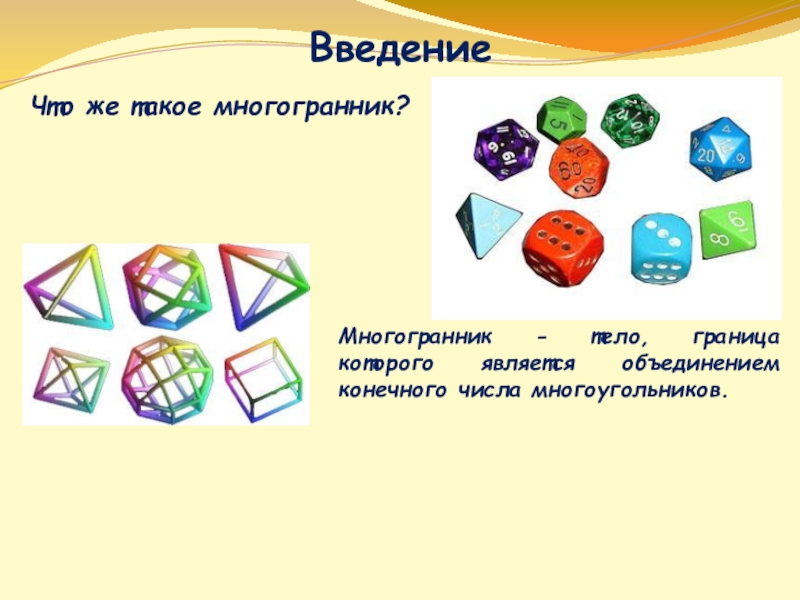
- 3. ВведениеЧто же такое многогранник?Многогранник - тело, граница которого является объединением конечного числа многоугольников.
- 4. История появления многогранников
- 5. Многогранники обладают богатой историей,
- 6. Первые упоминания о многогранниках известны еще
- 7. Одной из первых и самых
- 8. Правильные многогранники (Платоновы тела)
- 9. Правильный многогранник — выпуклый многогранник с
- 10. Существует всего 5 видов правильных многогранников:Леонардом Эйлером
- 11. Правильные многогранники встречаются так же
- 12. Полуправильные многогранники (архимедовы тела)
- 13. Слайд 13
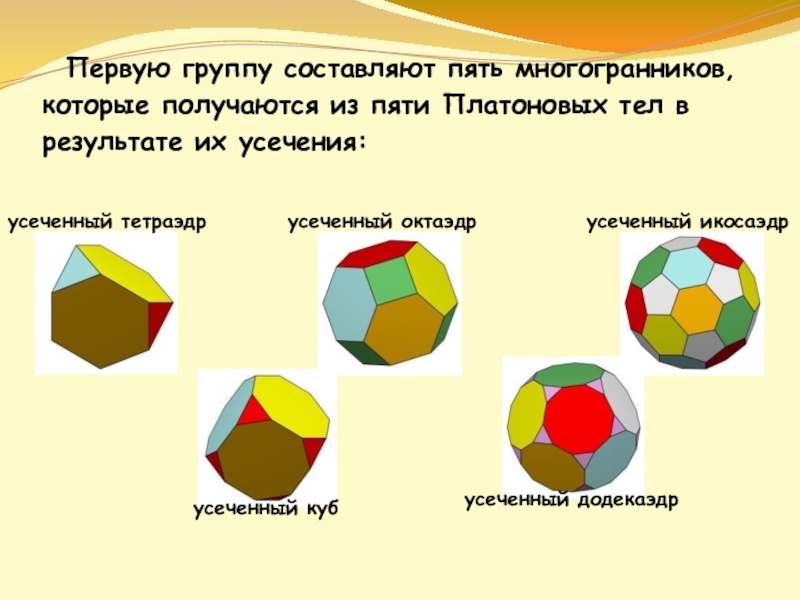
- 14. Первую группу составляют пять многогранников, которые
- 15. В четвертую группу входят две
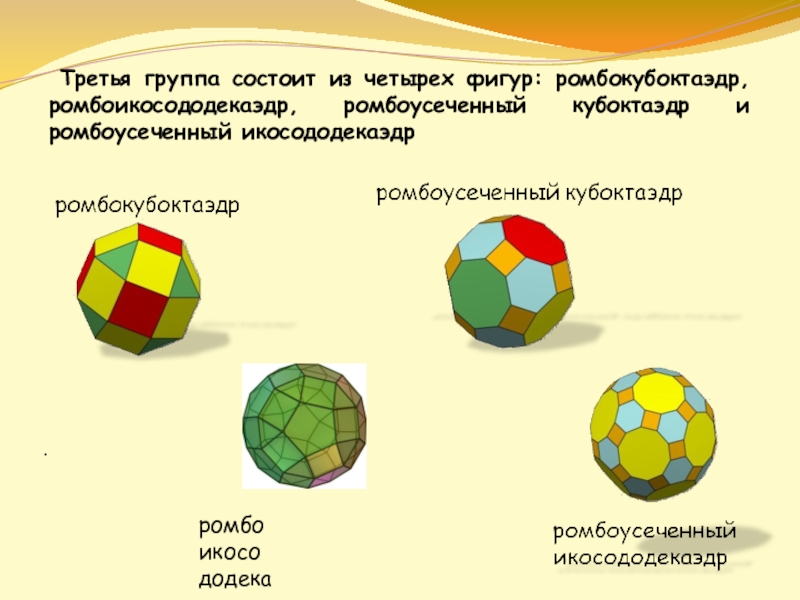
- 16. . Третья группа состоит из четырех фигур: ромбокубоктаэдр, ромбоикосододекаэдр, ромбоусеченный кубоктаэдр и ромбоусеченный икосододекаэдрромбоикосододекаэдр
- 17. Звездчатые многогранники
- 18. Звёздчатый многогранник — это выпуклый многогранник,
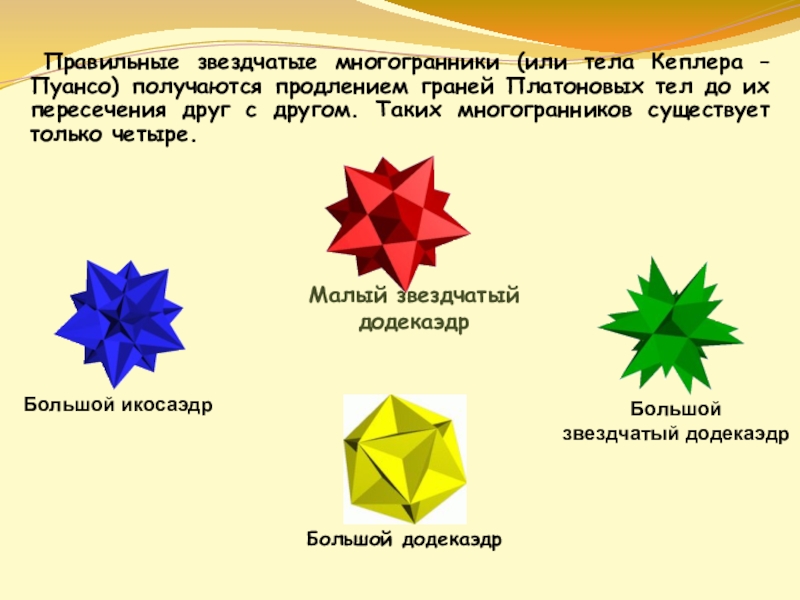
- 19. Правильные звездчатые многогранники (или тела Кеплера
- 20. Заключение Тема о многогранниках до сих пор
Слайд 2Содержание
Введение
История появления многогранников
Правильный многогранник и его виды
Правильные многогранники в природе
Полуправильные многогранники
Звездчатые
Заключение
Литература
Слайд 3Введение
Что же такое многогранник?
Многогранник - тело, граница которого является объединением конечного
Слайд 5 Многогранники обладают богатой историей, которая связана с именами
Слайд 6 Первые упоминания о многогранниках известны еще за три тысячи лет
Статистические данные
пирамиды Хеопса
Пирамида Хеопса в XIX веке
Высота (сегодня): ≈ 138,75 м
Длина боковой грани : ≈ 225 м
Длина сторон основания пирамиды:
юг — 230,454 м; север — 230,253 м;
запад — 230,357 м; восток — 230,394 м.
Площадь основания: ≈ 53 000 м² (5,3 га)
Площадь пирамиды: ≈ 85 500 m²
Периметр: 922 м.
Слайд 7 Одной из первых и самых известных школ была Пифагорейская,
Вселенная - додекаэдр
Земля - куб
Огонь - тетраэдр
Вода - икосаэдр
Воздух - октаэдр
Слайд 9 Правильный многогранник — выпуклый многогранник с максимально возможной симметрией, все
Каждый из правильных многоранников может быть охарактеризован следующими параметрами:
1) число граней.
2) число рёбер.
3) число вершин.
Слайд 10Существует всего 5 видов правильных многогранников:
Леонардом Эйлером была выведена формула, связывающая
В + Г = Р + 2
Слайд 11 Правильные многогранники встречаются так же и в живой природе.
Правильные многогранники – одни из самых распространённых фигур в природе. Подтверждением тому служит форма некоторых кристаллов.
Слайд 13 Полуправильные многогранники
1) Все грани являются правильными многоугольниками двух или более типов.
2) Для любой пары вершин существует симметрия многогранника переводящая одну вершину в другую.
3) В каждой вершине полуправильного многогранника сходится не более 5 рёбер.
Все полуправильные многогранники можно разделить на четыре группы.
Слайд 14 Первую группу составляют пять многогранников, которые получаются из пяти Платоновых
Слайд 15 В четвертую группу входят две курносые модификации - курносый
Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии.
Слайд 16.
Третья группа состоит из четырех фигур: ромбокубоктаэдр, ромбоикосододекаэдр, ромбоусеченный
ромбоикосододекаэдр
Слайд 18 Звёздчатый многогранник — это выпуклый многогранник, обладающий пирамидальными формами. Звёздчатые
1)неправильные многогранники (подавляющее большинство) 2)полуправильные, именуемые в дань исследовавшим их математикам «телами Кеплера -Пуансо».
Слайд 19 Правильные звездчатые многогранники (или тела Кеплера – Пуансо) получаются продлением
Малый звездчатый
додекаэдр