- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку:Аксиомы стереометрии .
Содержание
- 1. Презентация к уроку:Аксиомы стереометрии .
- 2. ГеометрияПланиметрияСтереометрия stereos Телесний, твердый, объемний, пространственный.
- 3. Стереометрия.Раздел геометрии, в котором изучаются свойства фигур в пространстве.Основные фигуры в пространстве:АТочка.аПрямая.Плоскость.
- 4. ТочкаПрямаяПлоскость A, B, C, …a, b, c, …абоAВ, BС, CD, …Стереометрия.
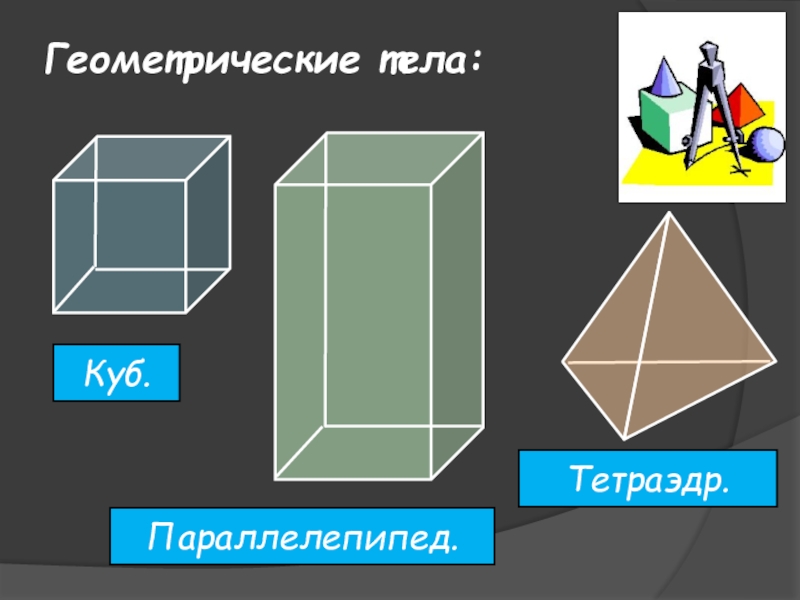
- 5. Геометрические тела:Куб.Параллелепипед.Тетраэдр.
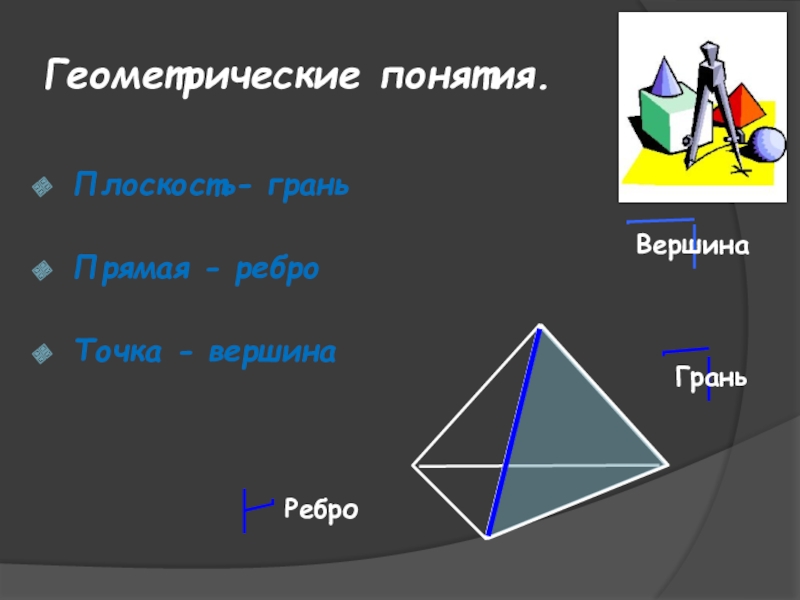
- 6. Геометрические понятия.Плоскость- грань Прямая - ребро Точка - вершинаВершинаГраньРебро
- 7. Аксиома( с греческого axíõma - принятие положения)Утверждение, которое принимается без доказательства.
- 8. АксиомыПланиметрияСтереометрия1. Каждой прямой принадлежат хотя бы две
- 9. А3. Если две плоскости имеют общую точку,
- 10. Аксиомы стереометрии описывают:А1.А2. А3. АВСβСпособ определения плоскости.βАВВзаимное размещение прямой и плоскостиαβВзаимное размещение плоскостей.
- 11. Способы определения плоскости1. Плоскость можно провести через
- 12. Взаимное расположение прямой и плоскости.Пряма я лежит
- 13. Следствия из аксиом стереометрииЧерез прямую и точку,которая
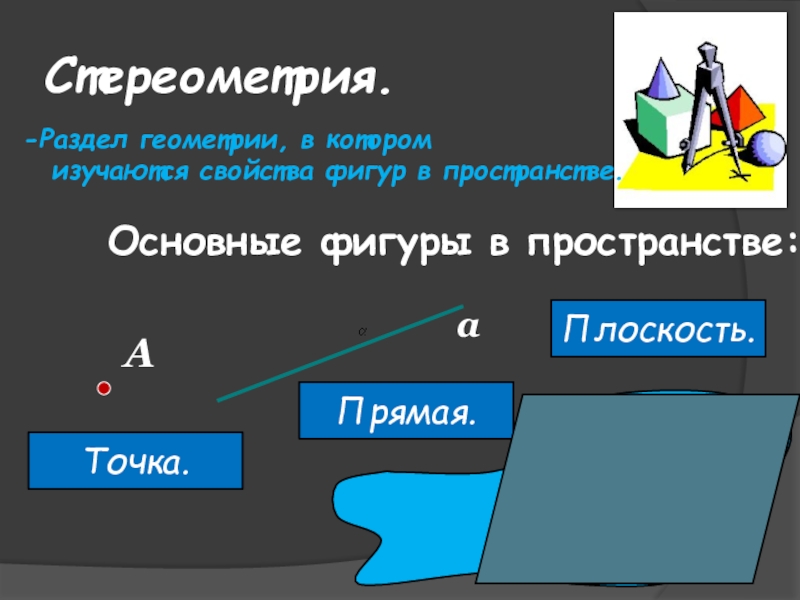
Слайд 3Стереометрия.
Раздел геометрии, в котором
изучаются свойства фигур в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Прямая.
Плоскость.
Слайд 7Аксиома
( с греческого axíõma - принятие положения)
Утверждение, которое принимается без доказательства.
Слайд 8Аксиомы
Планиметрия
Стереометрия
1. Каждой прямой принадлежат хотя бы две точки
2. Есть хотя бы
3. Через две точки проходит прямая и при том только одна.
Характеризует взаимное расположение точек и прямых.
Основное понятие геометрии
4. Из трех точек одна и только одна лежит между двумя другими.
А1. Через три точки,что не лежат на одной прямой проходит плоскость и при том только одна.
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
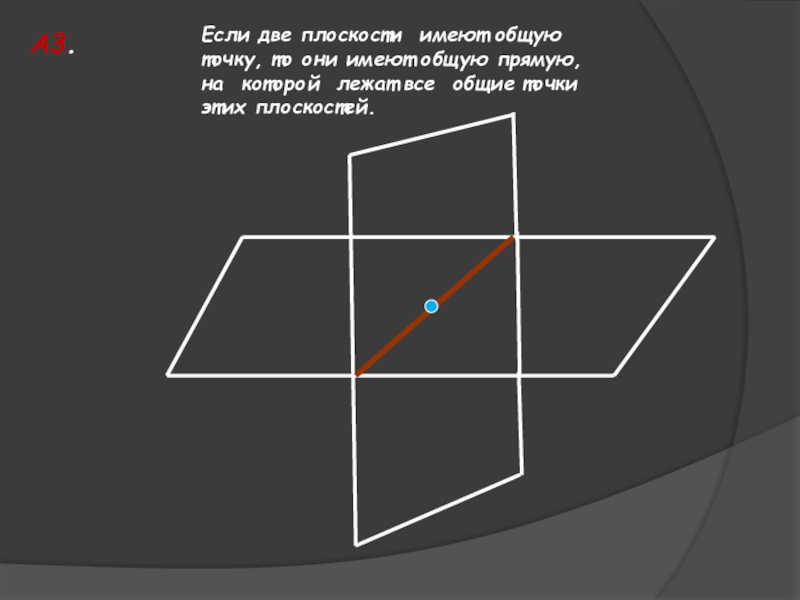
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Слайд 9
А3.
Если две плоскости имеют общую точку, то они имеют общую
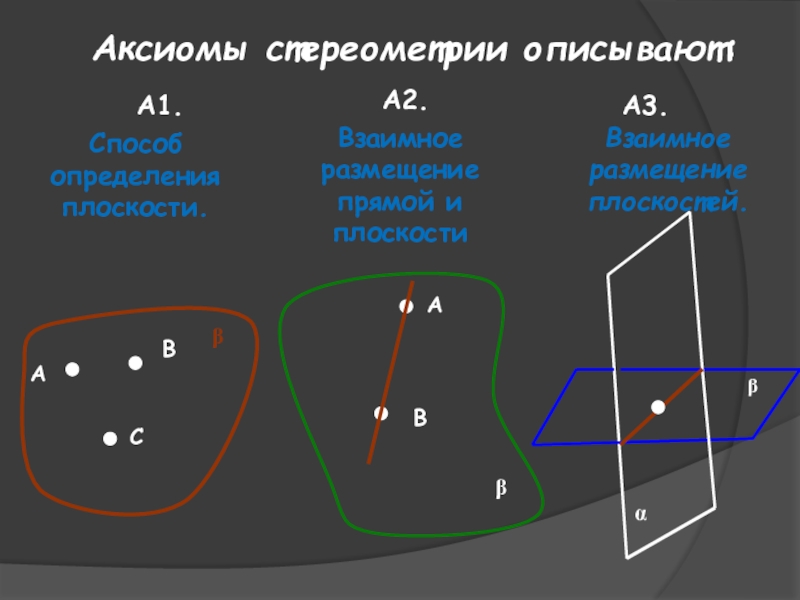
Слайд 10Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
β
Способ определения плоскости.
β
А
В
Взаимное размещение прямой и плоскости
α
β
Взаимное
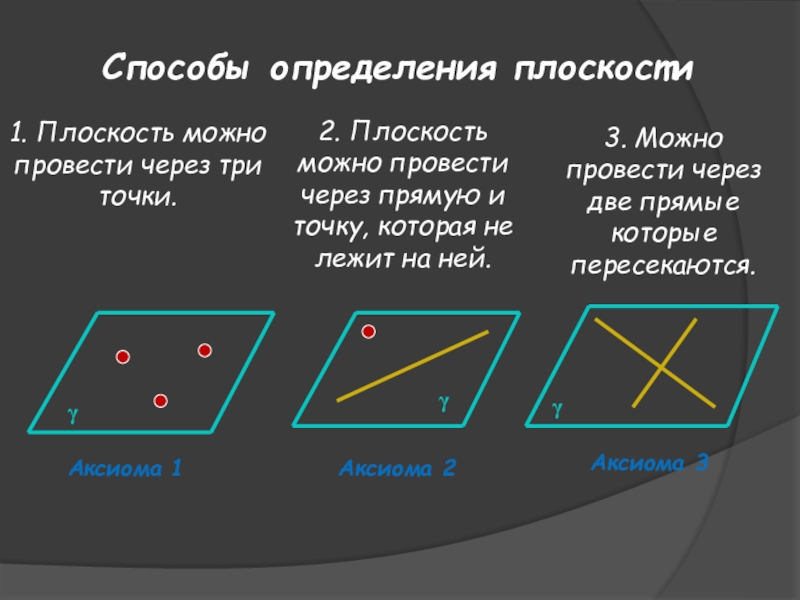
Слайд 11Способы определения плоскости
1. Плоскость можно провести через три точки.
2. Плоскость можно
Аксиома 1
Аксиома 2
Аксиома 3
3. Можно провести через две прямые которые пересекаются.
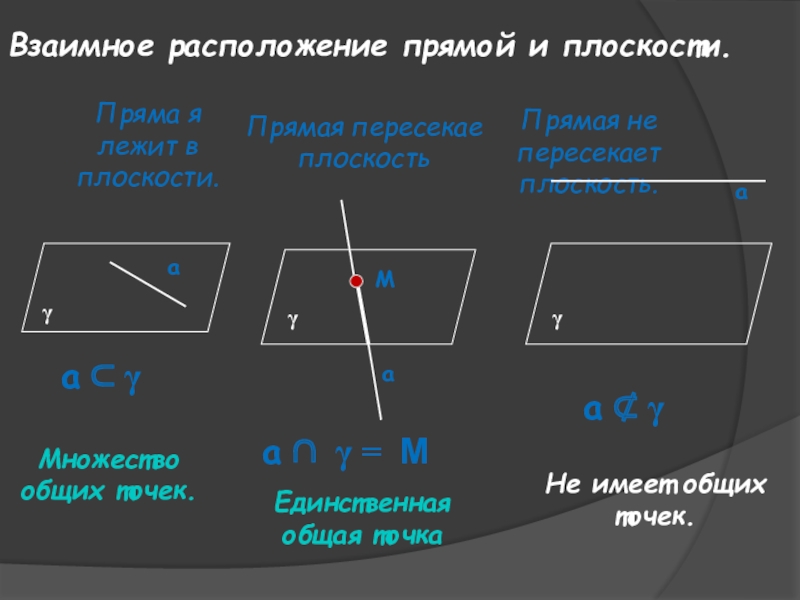
Слайд 12Взаимное расположение прямой и плоскости.
Пряма я лежит в плоскости.
Прямая пересекае плоскость
Прямая
Множество общих точек.
Единственная общая точка
Не имеет общих точек.
γ
а
γ
а
М
γ
а
а ⊂ γ
а ∩ γ = М
а ⊄ γ
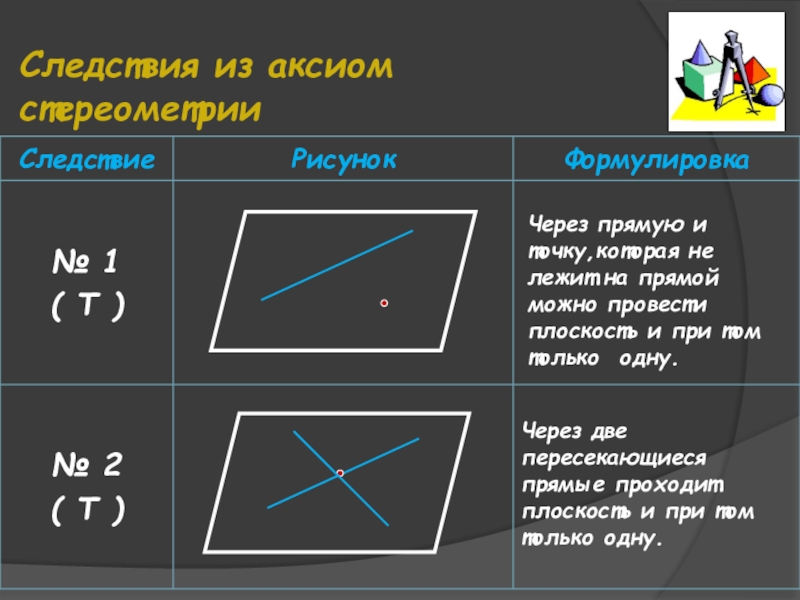
Слайд 13Следствия из аксиом стереометрии
Через прямую и точку,которая не лежит на прямой
Через две пересекающиеся прямые проходит плоскость и при том только одну.