- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку в 11 классе по теме Площадь криволинейной трапеции
Содержание
- 1. Презентация к уроку в 11 классе по теме Площадь криволинейной трапеции
- 2. Криволине́йная трапе́ция — плоская фигура, ограниченная графиком
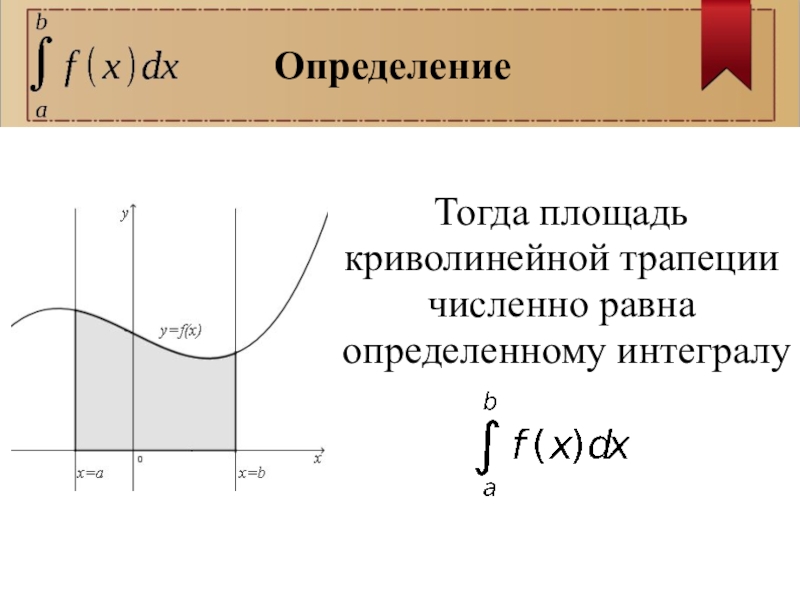
- 3. Тогда площадь криволинейной трапеции численно равна определенному интегралу Определение
- 4. Определенный интеграл вычисляется по формуле Ньютона-Лейбница
- 5. Вычислим площадь фигуры, ограниченной линиями: y =
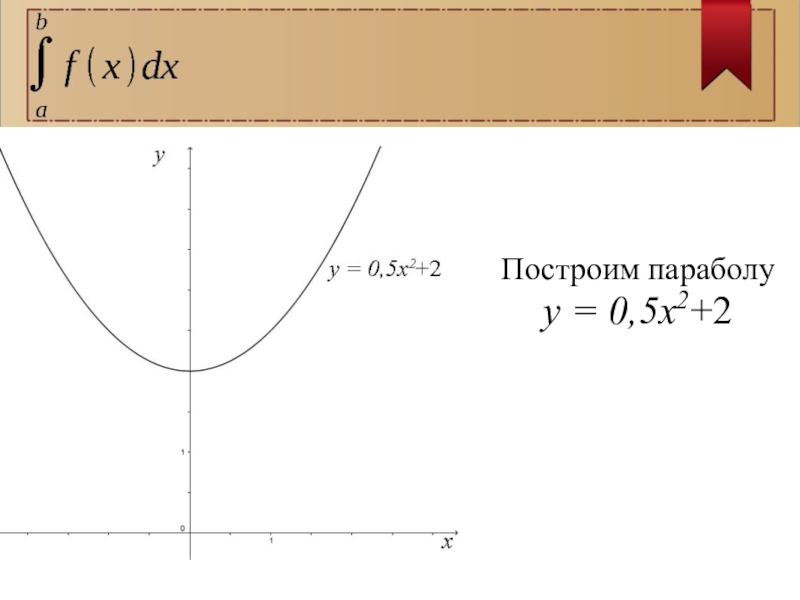
- 6. Построим параболуy = 0,5x2+2
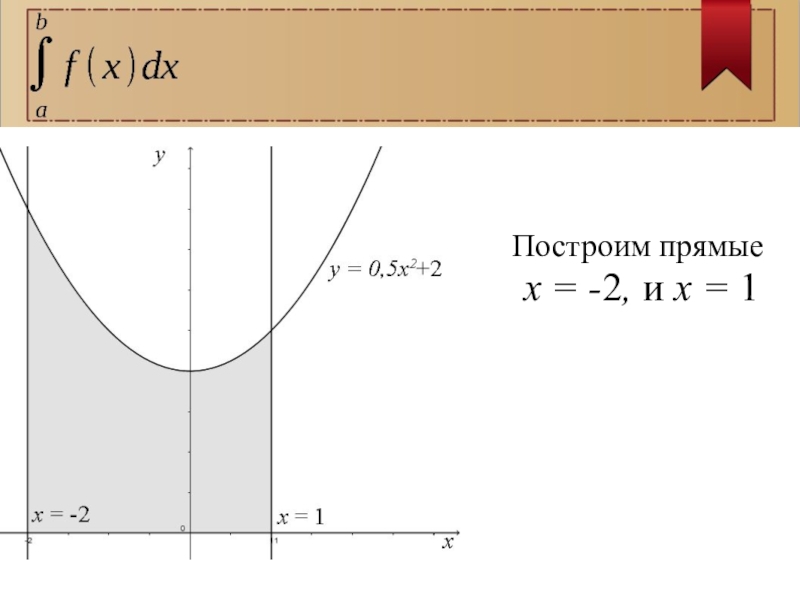
- 7. Построим прямые x = -2, и x = 1
- 8. С помощью формулы Ньютона-Лейбница вычислим площадь данной криволинейной трапеции
- 9. С помощью формулы Ньютона-Лейбница вычислим площадь данной криволинейной трапеции
- 10. С помощью формулы Ньютона-Лейбница вычислим площадь данной криволинейной трапеции
- 11. С помощью формулы Ньютона-Лейбница вычислим площадь данной
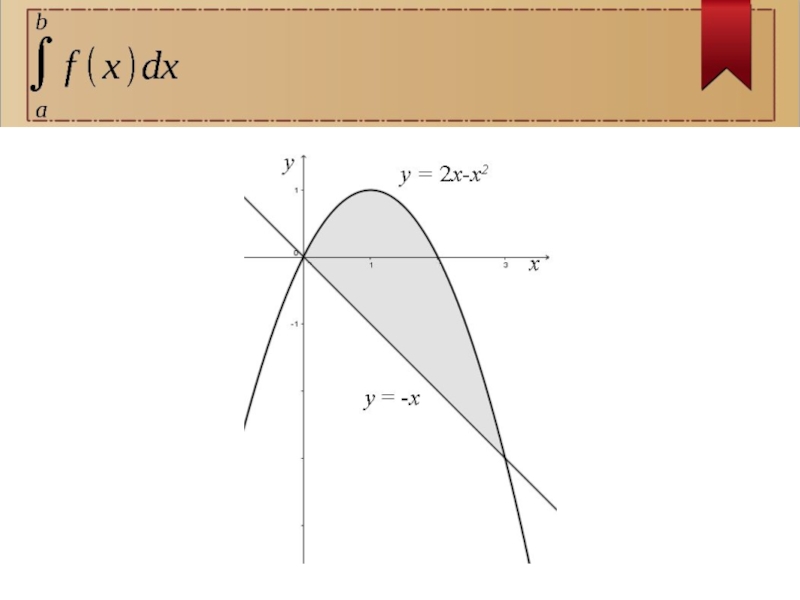
- 12. Вычислим площадь фигуры, ограниченной линиями: y = 2х-x2, y = -x .Пример 2
- 13. Найдем точки пересечения параболыy = 2х-x2 и
- 14. Если на отрезке [a;b] некоторая непрерывная функция
- 15. Слайд 15
- 16. Искомая фигура ограничена параболой y = 2х-x2
- 17. 1) Если необходимо найти определенный интеграл, то
Криволине́йная трапе́ция — плоская фигура, ограниченная графиком непрерывной функции y = f(x), определенной на отрезке [a; b], осью абсцисс и прямыми x = a и x = b.Определение
Слайд 2Криволине́йная трапе́ция — плоская фигура, ограниченная графиком непрерывной функции y =
f(x), определенной на отрезке [a; b], осью абсцисс и прямыми x = a и x = b.
Определение
![Криволине́йная трапе́ция — плоская фигура, ограниченная графиком непрерывной функции y = f(x), определенной на отрезке [a; b],](/img/thumbs/2e0867085ab4b6b7e7404666cc5d251f-800x.jpg "Презентация к уроку в 11 классе по теме Площадь криволинейной трапеции Криволине́йная трапе́ция — плоская фигура, ограниченная графиком непрерывной функции y =")
Слайд 5Вычислим площадь фигуры, ограниченной линиями:
y = 0,5x2+2, y = 0,
x = -2, x = 1.
Обратитим внимание, что
уравнение y = 0 задает ось ОХ
Обратитим внимание, что
уравнение y = 0 задает ось ОХ
Пример 1
Слайд 11С помощью формулы Ньютона-Лейбница вычислим площадь данной криволинейной трапеции
Ответ:
кв.ед.
Слайд 13Найдем точки пересечения параболы
y = 2х-x2 и прямой y = -x
Для
этого решим уравнение
2х-x2 = -x
3х-x2 = 0
х(3-х)=0
х1=0 и х2=3
Значит, нижний предел интегрирования а=0, верхний предел интегрирования b=3.
2х-x2 = -x
3х-x2 = 0
х(3-х)=0
х1=0 и х2=3
Значит, нижний предел интегрирования а=0, верхний предел интегрирования b=3.
Слайд 14Если на отрезке [a;b] некоторая непрерывная функция f(x) больше либо равна
некоторой непрерывной функции g(x), то площадь фигуры, ограниченной графиками данных функций и прямыми x=a, x=b, можно найти по формуле:
![Если на отрезке [a;b] некоторая непрерывная функция f(x) больше либо равна некоторой непрерывной функции g(x), то площадь](/img/thumbs/3cd51f5a644bdb6419b14b185220c369-800x.jpg "Презентация к уроку в 11 классе по теме Площадь криволинейной трапеции Если на отрезке [a;b] некоторая непрерывная функция f(x) больше либо равна")
Слайд 16Искомая фигура ограничена параболой y = 2х-x2 сверху и прямой y
= снизу.
На отрезке [0;3] 2х-x2 ≥ -x, по соответствующей формуле:
На отрезке [0;3] 2х-x2 ≥ -x, по соответствующей формуле:
Ответ: кв.ед.
![Искомая фигура ограничена параболой y = 2х-x2 сверху и прямой y = снизу.На отрезке [0;3] 2х-x2 ≥](/img/thumbs/4246da090c5617b175b201fd7f3bc754-800x.jpg "Презентация к уроку в 11 классе по теме Площадь криволинейной трапеции Искомая фигура ограничена параболой y = 2х-x2 сверху и прямой y")
Слайд 171) Если необходимо найти определенный интеграл, то он может быть отрицательным.
2)
Если необходимо найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна!
Важно!
