- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку: Цилиндр, 11 класс.
Содержание
- 1. Презентация к уроку: Цилиндр, 11 класс.
- 2. Подготовила: Учитель математики : Куракина Н. Н.МОУ «СОШ №7»На тему:Тела вращения, цилиндр его понятие и свойства.
- 3. Понятие цилиндра
- 4. О1ОАА1М1Мαβ Ось цилиндраL1L1. Цилиндрическая
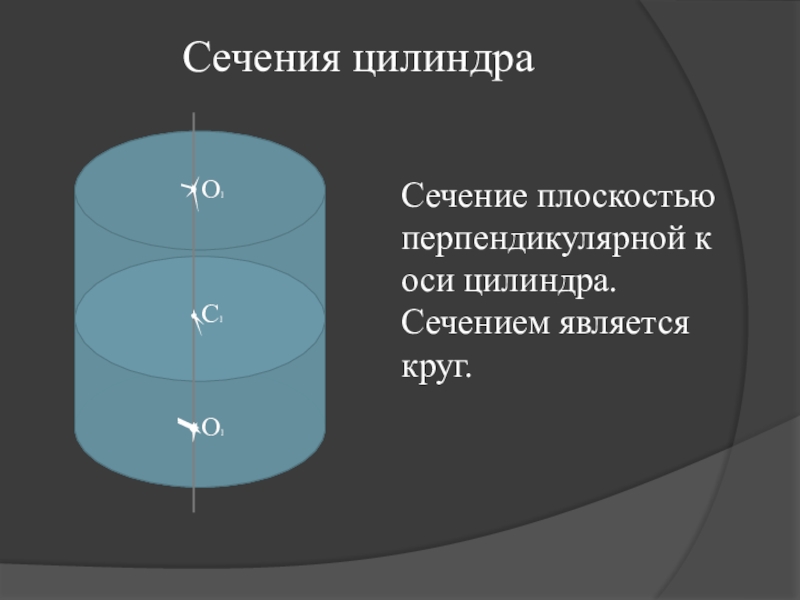
- 5. О1С1О1Сечение плоскостью перпендикулярной к оси цилиндра. Сечением является круг.Сечения цилиндра
- 6. СDВАОО1Осевое сечение – сечение плоскостью, проходящей через
- 7. СDВАПрямым круговым цилиндром называется фигура, полученная при
- 8. αАВВ1А1О1ОКасательная плоскость цилиндра Касательная плоскость цилиндра –
- 9. 2πrАА1ВВ1НРАЗВЕРТКАРазвертка цилиндра -
- 10. Решение задач с участием ЦИЛИНДРА.Задача №1.
- 11. Задача №2АВСDО1ОRНДано: АВСD – осевое сечение; SАВСD
- 12. Задача №3ОО1АВСDНДано: АВСD ос. сечение, квадрат
- 13. Конец
Слайд 2Подготовила:
Учитель математики : Куракина Н. Н.
МОУ «СОШ №7»
На тему:
Тела вращения,
Слайд 4
О1
О
А
А1
М1
М
α
β
Ось цилиндра
L1
L
1. Цилиндрическая поверхность:
Отрезки
2. Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется цилиндром.
Цилиндрическая поверхность – поверхность цилиндра, круги – основания цилиндра, прямая ОО1 – ось цилиндра.
Все образующие цилиндра параллельны и равны друг другу как отрезки параллельных прямых, заключенные между параллельными плоскостями α и β: АА1II ММ1 и АА1 = ММ1
Длина образующей – высота цилиндра, радиус АА1 = Н и ОМ = r.
Основание Y
Основание Y
Слайд 5
О1
С1
О1
Сечение плоскостью перпендикулярной к оси цилиндра. Сечением является круг.
Сечения цилиндра
Слайд 6
С
D
В
А
О
О1
Осевое сечение – сечение плоскостью, проходящей через ось цилиндра.
Сечением является прямоугольник,
АВСD – сечение осевое
АВ = СD = L (образующие)
ВС = АD = d (диаметр)
Слайд 7
С
D
В
А
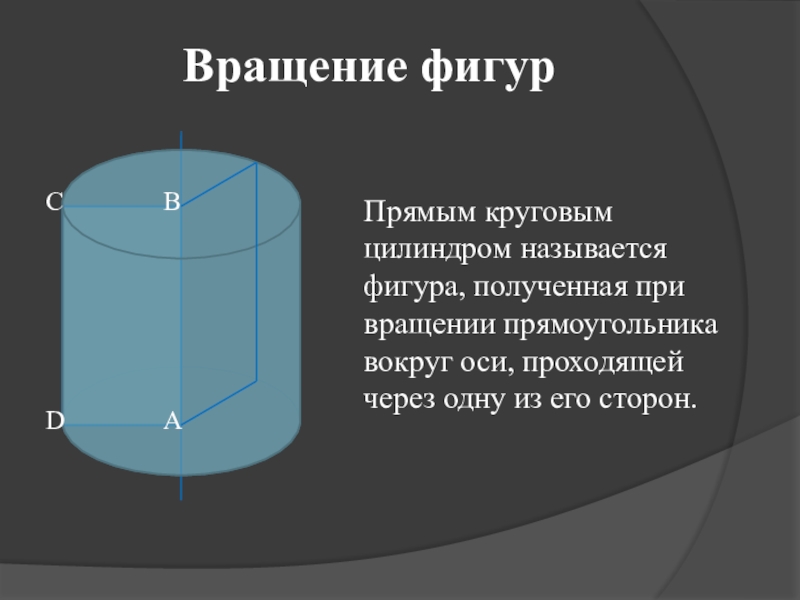
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси,
Вращение фигур
Слайд 8
α
А
В
В1
А1
О1
О
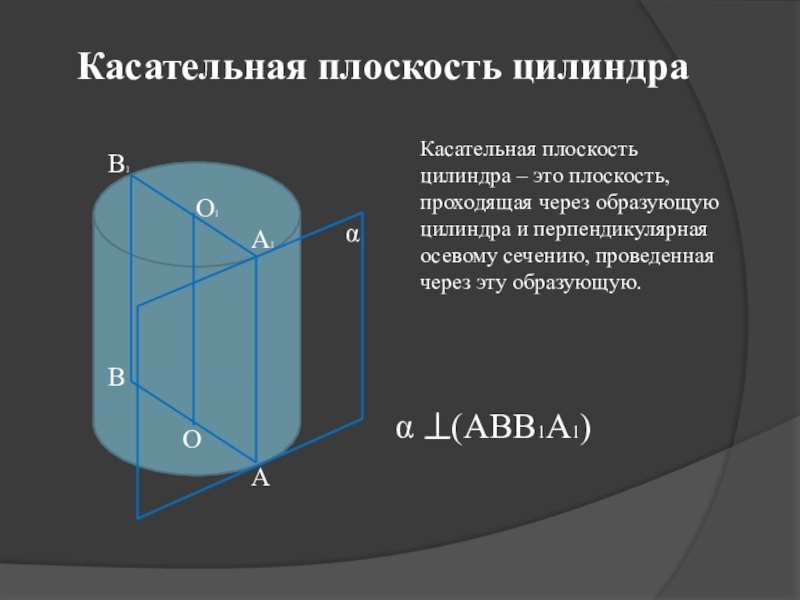
Касательная плоскость цилиндра
Касательная плоскость цилиндра – это плоскость, проходящая через
α
(АВВ1А1)
Слайд 9
2πr
А
А1
В
В1
Н
РАЗВЕРТКА
Развертка цилиндра - прямоугольник и является боковой
Площадь боковой поверхности цилиндра есть площадь её поверхности.
Sпр АВВ1А1 = АА1 * АВ
Sбок = 2πr * Н
Произведение длины окружности на высоту.
Sпол – сумма площадей боковой поверхности и двух оснований
Sцил = 2πr2 + 2πr * H = 2πr( r + H)
Sосн = πr2 =>
Слайд 10Решение задач с участием
ЦИЛИНДРА.
Задача №1.
Дано: АС = d
<
Найти: Sцил.
Решение:
45о
А
В
С
О
Δ АВС – прямоугольный
ВАС = 45о => ΔАВС – равнобедренный, значит АВ = ВС = 5, Н = 5
т.к. АС = d, => АС = 2R , R = 2,5
Sпол = 2πR (R + Н)
Sпол = 2πR * 2,5 (2,5 + 5) = 5π * 7,5 = 37,5π
<
Ответ: 37,5см
Слайд 11Задача №2
А
В
С
D
О1
О
R
Н
Дано: АВСD – осевое сечение; SАВСD = 10 м2;
Найти: Н - ?
Решение:
S осн = πr2 = 5
S сеч = 2R * H = 10 => R = 10 : (2 * Н) = 5 : Н
πR2 = 5
π * (5 : Н)2 = 5
Н2 = 5π
Н = 5π см
Ответ:
5π см.
Слайд 12Задача №3
О
О1
А
В
С
D
Н
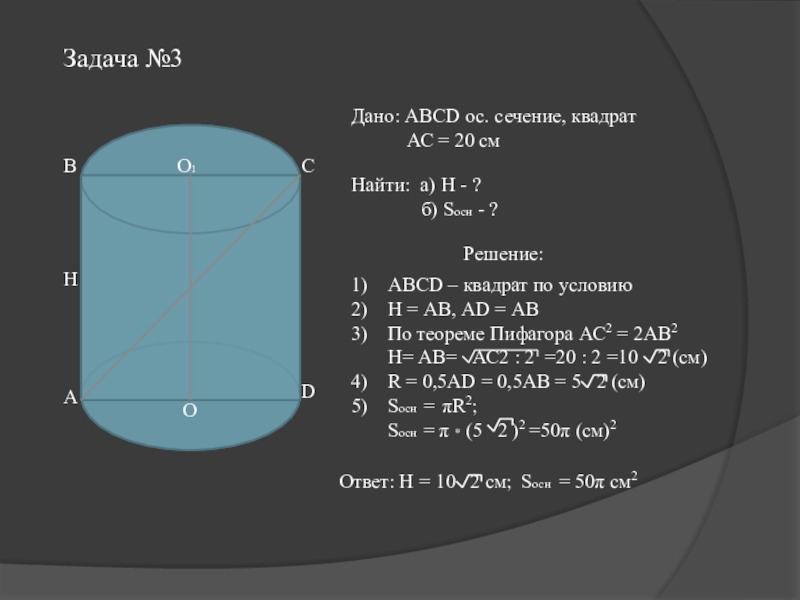
Дано: АВСD ос. сечение, квадрат
Найти: а) Н - ?
б) Sосн - ?
Решение:
АВСD – квадрат по условию
Н = АВ, АD = АВ
По теореме Пифагора АС2 = 2АВ2 Н= АВ= АС2 : 2 =20 : 2 =10 2 (см)
R = 0,5АD = 0,5АВ = 5 2 (см)
Sосн = πR2;
Sосн = π * (5 2 )2 =50π (см)2
Ответ: Н = 10 2 см; Sосн = 50π см2