Юлия
Учитель математики: Ахметов Ф.Г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Треугольники. Первый признак равенства треугольников
Содержание
- 1. Презентация к уроку Треугольники. Первый признак равенства треугольников
- 2. Треугольник — это геометрическая фигура, Образованная тремя отрезками,
- 3. Если два треугольника можно совместить наложением, их
- 4. Первый признак равенства треугольниковЕсли две стороны и
- 5. Решение задач Задача №11) Дано: AB=AD, ∠BAC=∠DAC Доказать:
- 6. Задача №2Дано:AO=BO, CO=DOДоказать: ∆AOC=∆BOD.Доказательство:Определяем те элементы, о
- 7. Использованная литература и программы1. Геометрия. 7—9
- 8. СПАСИБО ЗА ВНИМАНИЕ
Треугольник — это геометрическая фигура, Образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника.Обозначение треугольника:Δ ABC или Δ BCA или буквы вершин в любом другом
Слайд 1Треугольник.
Первый признак равенства треугольников.
Выполнила ученица 7«а» класс
МБОУ СОШ №24 г.Йошкар-Ола
Соколова
Слайд 2 Треугольник — это геометрическая фигура,
Образованная тремя отрезками, которые соединяют три
не
лежащие на одной прямой точки.
Три точки, образующие треугольник, называются вершинами треугольника, а отрезки —
сторонами треугольника.
Обозначение треугольника:
Δ ABC или Δ BCA или буквы вершин в любом другом порядке.
Обозначение угла:
∠ A, ∠BAC или ∠ CAB.
Обозначение стороны: AB или BA.
Сторону, которая лежит напротив угла, называют противолежащей углу и угол называют противолежащим стороне.
Углы, которые имеет одну общую сторону, называют прилежащими этой стороне.
Сумма сторон треугольника называется периметром.
Три точки, образующие треугольник, называются вершинами треугольника, а отрезки —
сторонами треугольника.
Обозначение треугольника:
Δ ABC или Δ BCA или буквы вершин в любом другом порядке.
Обозначение угла:
∠ A, ∠BAC или ∠ CAB.
Обозначение стороны: AB или BA.
Сторону, которая лежит напротив угла, называют противолежащей углу и угол называют противолежащим стороне.
Углы, которые имеет одну общую сторону, называют прилежащими этой стороне.
Сумма сторон треугольника называется периметром.
Слайд 3
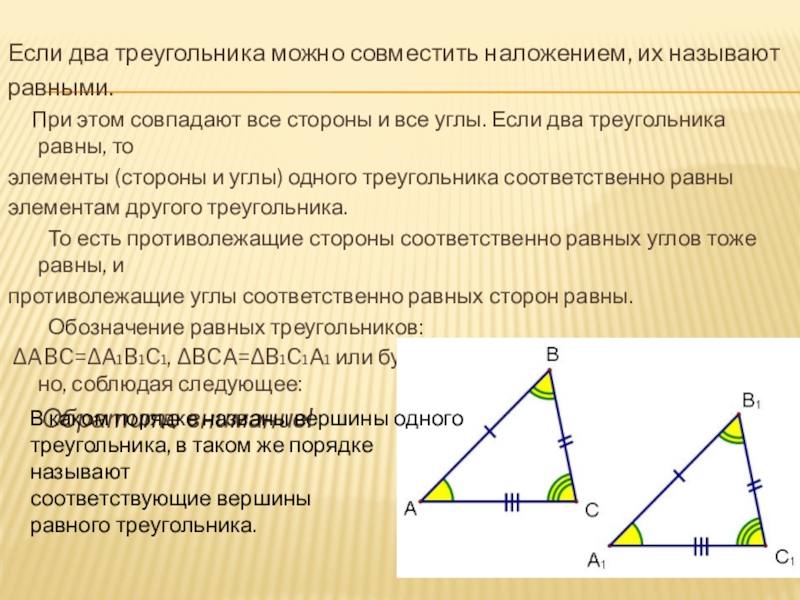
Если два треугольника можно совместить наложением, их называют
равными.
При этом совпадают все стороны и все углы. Если два треугольника равны, то
элементы (стороны и углы) одного треугольника соответственно равны
элементам другого треугольника.
То есть противолежащие стороны соответственно равных углов тоже равны, и
противолежащие углы соответственно равных сторон равны.
Обозначение равных треугольников:
ΔABC=ΔA1B1C1, ΔBCA=ΔB1C1A1 или буквы вершин в любом другом порядке, но, соблюдая следующее:
Обратите внимание!
элементы (стороны и углы) одного треугольника соответственно равны
элементам другого треугольника.
То есть противолежащие стороны соответственно равных углов тоже равны, и
противолежащие углы соответственно равных сторон равны.
Обозначение равных треугольников:
ΔABC=ΔA1B1C1, ΔBCA=ΔB1C1A1 или буквы вершин в любом другом порядке, но, соблюдая следующее:
Обратите внимание!
В каком порядке названы вершины одного
треугольника, в таком же порядке называют
соответствующие вершины
равного треугольника.
Слайд 4Первый признак равенства треугольников
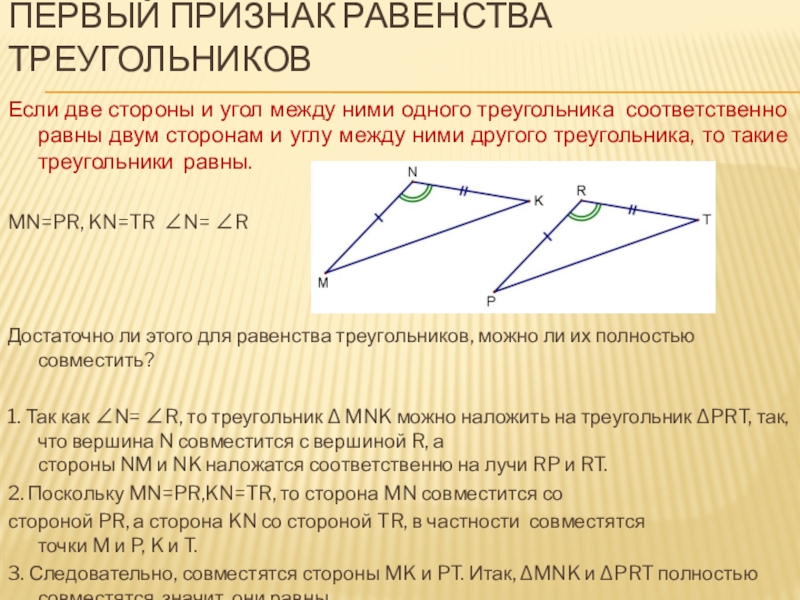
Если две стороны и угол между ними одного
треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
MN=PR, KN=TR ∠N= ∠R
Достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
1. Так как ∠N= ∠R, то треугольник Δ MNK можно наложить на треугольник ΔPRT, так, что вершина N совместится с вершиной R, а стороны NM и NK наложатся соответственно на лучи RP и RT.
2. Поскольку MN=PR,KN=TR, то сторона MN совместится со
стороной PR, а сторона KN со стороной TR, в частности совместятся точки M и P, K и T.
3. Следовательно, совместятся стороны MK и PT. Итак, ΔMNK и ΔPRT полностью совместятся, значит, они равны.
MN=PR, KN=TR ∠N= ∠R
Достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
1. Так как ∠N= ∠R, то треугольник Δ MNK можно наложить на треугольник ΔPRT, так, что вершина N совместится с вершиной R, а стороны NM и NK наложатся соответственно на лучи RP и RT.
2. Поскольку MN=PR,KN=TR, то сторона MN совместится со
стороной PR, а сторона KN со стороной TR, в частности совместятся точки M и P, K и T.
3. Следовательно, совместятся стороны MK и PT. Итак, ΔMNK и ΔPRT полностью совместятся, значит, они равны.
Слайд 5Решение задач
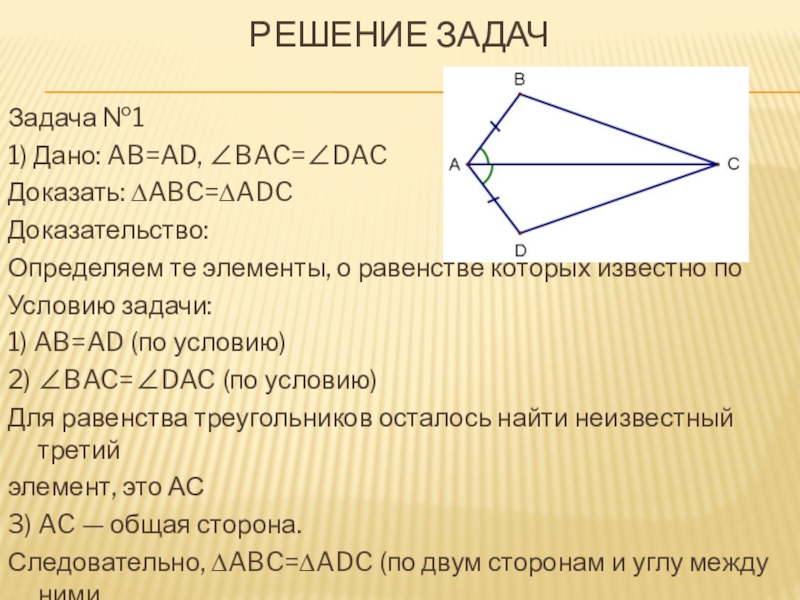
Задача №1
1) Дано: AB=AD, ∠BAC=∠DAC
Доказать: ∆ABC=∆ADC
Доказательство:
Определяем те элементы, о
равенстве которых известно по
Условию задачи:
1) AB=AD (по условию)
2) ∠BAC=∠DAC (по условию)
Для равенства треугольников осталось найти неизвестный третий
элемент, это АС
3) AC — общая сторона.
Следовательно, ∆ABC=∆ADC (по двум сторонам и углу между ними,
то есть по первому признаку равенства треугольников).
Условию задачи:
1) AB=AD (по условию)
2) ∠BAC=∠DAC (по условию)
Для равенства треугольников осталось найти неизвестный третий
элемент, это АС
3) AC — общая сторона.
Следовательно, ∆ABC=∆ADC (по двум сторонам и углу между ними,
то есть по первому признаку равенства треугольников).
Слайд 6
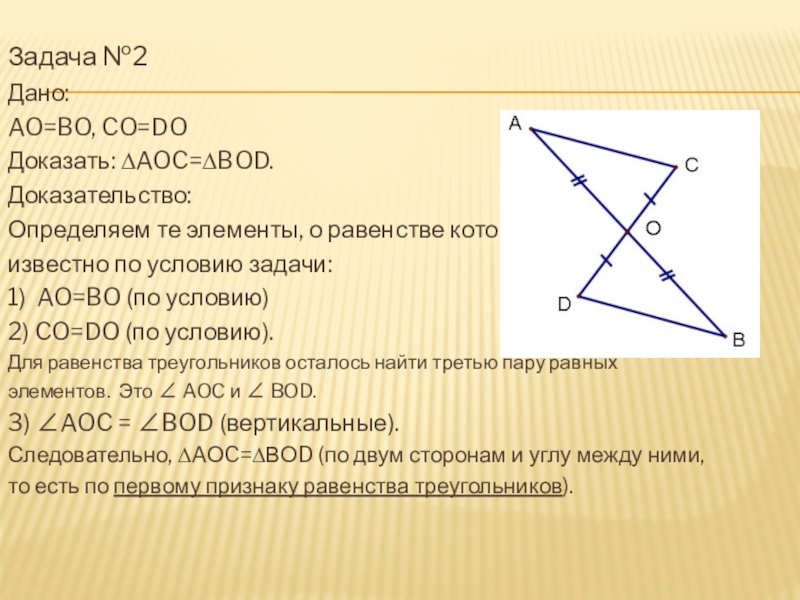
Задача №2
Дано:
AO=BO, CO=DO
Доказать: ∆AOC=∆BOD.
Доказательство:
Определяем те элементы, о равенстве которых
известно по
условию задачи:
1) AO=BO (по условию)
2) CO=DO (по условию).
Для равенства треугольников осталось найти третью пару равных
элементов. Это ∠ AOC и ∠ BOD.
3) ∠AOC = ∠BOD (вертикальные).
Следовательно, ∆AОC=∆ВОD (по двум сторонам и углу между ними,
то есть по первому признаку равенства треугольников).
1) AO=BO (по условию)
2) CO=DO (по условию).
Для равенства треугольников осталось найти третью пару равных
элементов. Это ∠ AOC и ∠ BOD.
3) ∠AOC = ∠BOD (вертикальные).
Следовательно, ∆AОC=∆ВОD (по двум сторонам и углу между ними,
то есть по первому признаку равенства треугольников).
Слайд 7Использованная литература
и программы
1. Геометрия. 7—9 классы : учеб, для общеобразовательных
организаций Л. С. Атанасян и др.,
2 Программа «Живая математика»
2 Программа «Живая математика»