- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Теорема Пифагора
Содержание
- 1. Презентация к уроку по теме Теорема Пифагора
- 2. «Геометрия владеет многими сокровищами: одно из них – это теорема Пифагора»
- 3. Сообщение об историитеоремы Пифагора
- 4. Сделайте измерения, заполните таблицу:Вывод?
- 5. Теорема Пифагора современная формулировка: В прямоугольном
- 6. Начертим прямоугольный треугольник
- 7. С другой стороныSABCD=4Sтр +SквSтр= ав; Sкв=c2SABCD=4* ав+с2=2ав+с2(а+в)2=2ав+с2а2+2ав+в2=2ав+с2а2+в2=с2ч.т.д.авсАВСDааавввсссcccc
- 8. Решение задач Составьте по рисунку, используя теорему
- 9. Подумайте! Можно ли применять теорему Пифагора
- 10. Итак, вопрос: На что надо обратить
- 11. Задача индийского математика XII века БхаскарыНа
- 12. «Случися некому человеку к стене лестницу прибрати,
- 13. Задача из китайской «Математики в девяти
- 14. Задача. Высота, опущенная из вершины В АВС,
- 15. Домашнее задание1. № 490, 491(а) 2. Найти другой способ доказательства теоремы Пифагора
- 16. Причина популярности теоремы Пифагора триедина – это красота, простота и значимость!
- 17. Пребудет Вечной истина, как скороЕё познает слабый
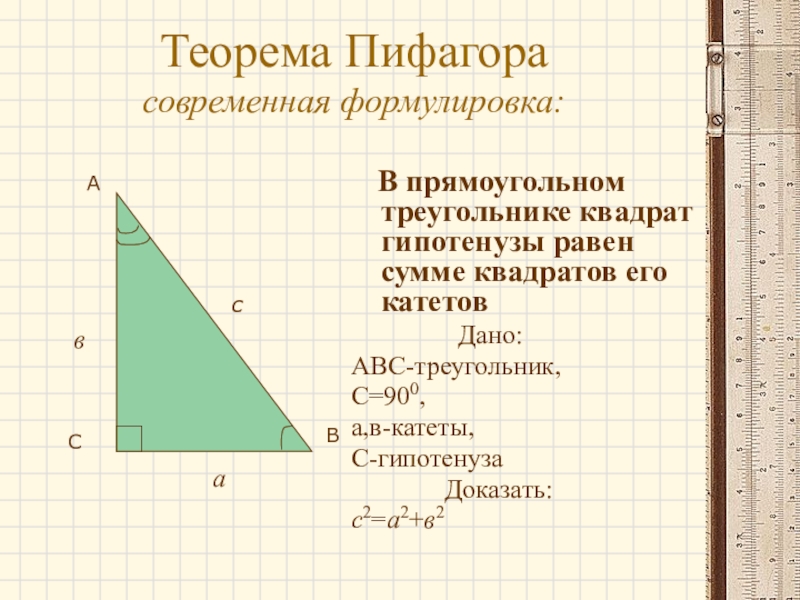
Слайд 5Теорема Пифагора
современная формулировка:
В прямоугольном треугольнике квадрат гипотенузы равен сумме
Дано:
АВС-треугольник,
С=900,
а,в-катеты,
С-гипотенуза
Доказать:
с2=а2+в2
А
В
С
с
а
в
Слайд 6 Начертим прямоугольный треугольник со сторонами а, в,
Достроим треугольник до квадрата со сторонами а+в.
Найдем площадь этого квадрата
S=(а + в)2
а
с
в
в
в
в
а
а
а
Доказательство:
Слайд 7С другой стороны
SABCD=4Sтр +Sкв
Sтр= ав;
Sкв=c2
SABCD=4* ав+с2=2ав+с2
(а+в)2=2ав+с2
а2+2ав+в2=2ав+с2
а2+в2=с2
ч.т.д.
а
в
с
А
В
С
D
а
а
а
в
в
в
с
с
с
c
c
c
c
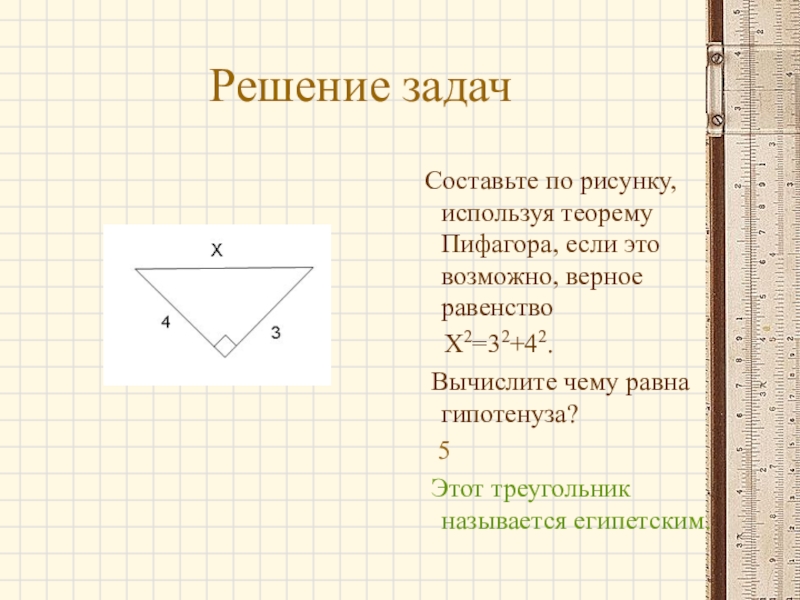
Слайд 8Решение задач
Составьте по рисунку, используя теорему Пифагора, если это возможно,
Х2=32+42.
Вычислите чему равна гипотенуза?
5
Этот треугольник называется египетским.
Слайд 9Подумайте!
Можно ли применять теорему Пифагора к этому треугольнику?
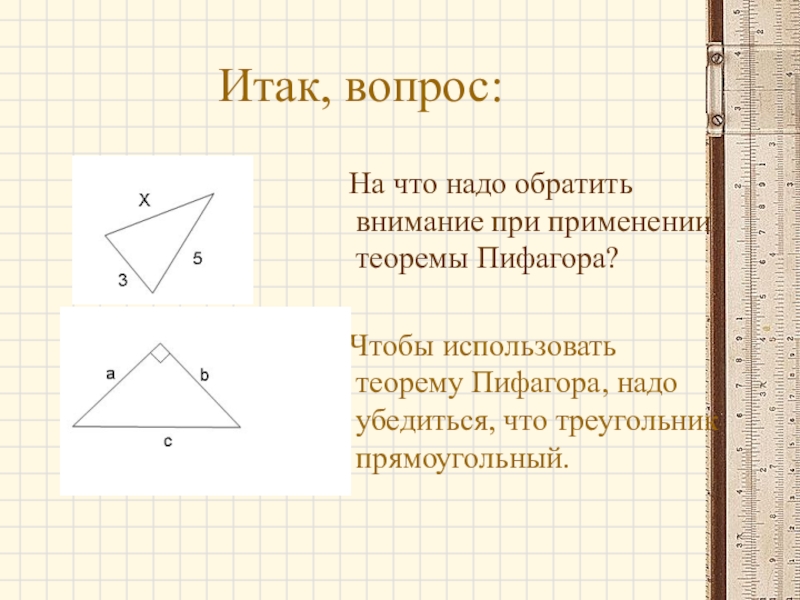
Слайд 10Итак, вопрос:
На что надо обратить внимание при применении теоремы
Чтобы использовать теорему Пифагора, надо убедиться, что треугольник прямоугольный.
Слайд 11Задача индийского математика
XII века Бхаскары
На берегу реки рос тополь одинокий.
Вдруг
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
?
5
Слайд 12«Случися некому человеку
к стене лестницу прибрати, стены же тоя высота
117 стоп. И обреете
лестницу долготью
125 стоп.
И ведати хочет,
колико стоп сея лестницы нижний конец от стены отстояти имать."
?
Задача из учебника "Арифметика"
Леонтия Магницкого
44
Слайд 13Задача из китайской
«Математики в девяти книгах»
Имеется водоем со стороной в
О
С
А
Ответ: 12 чи- глубина, 13 чи - длина камыша.
х
Х+1
5
В
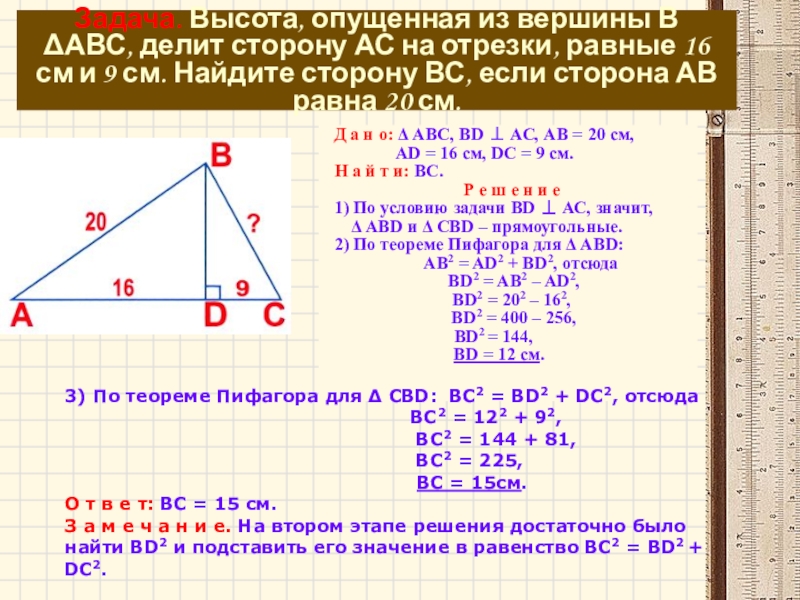
Слайд 14Задача. Высота, опущенная из вершины В АВС, делит сторону АС на
Д а н о: АВС, BD АС, АВ = 20 см,
AD = 16 см, DC = 9 см.
Н а й т и: ВС.
Р е ш е н и е
1) По условию задачи BD АС, значит,
ABD и CBD – прямоугольные.
2) По теореме Пифагора для ABD:
АВ2 = AD2 + BD2, отсюда
BD2 = AB2 – AD2,
BD2 = 202 – 162,
BD2 = 400 – 256,
BD2 = 144,
BD = 12 см.
3) По теореме Пифагора для СBD: ВС2 = ВD2 + DС2, отсюда
BC2 = 122 + 92,
BC2 = 144 + 81,
BC2 = 225,
BC = 15см.
О т в е т: ВС = 15 см.
З а м е ч а н и е. На втором этапе решения достаточно было найти BD2 и подставить его значение в равенство ВС2 = ВD2 + DС2.
Слайд 17Пребудет Вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора
Верна,
Обильно было жертвоприношение
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За свет луча, пришедший с облаков.
Поэтому всегда с тех самых пор
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Применеие теоремы Пифагора
в литературе