- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по теме Объем прямоугольной призмы.
Содержание
- 1. Презентация к уроку по теме Объем прямоугольной призмы.
- 2. Цели урока:Вспомнить понятие призмы.Изучить теорему об объеме призмы.Провести доказательство.Применить полученные знания на практике.Давайте уже начинать!
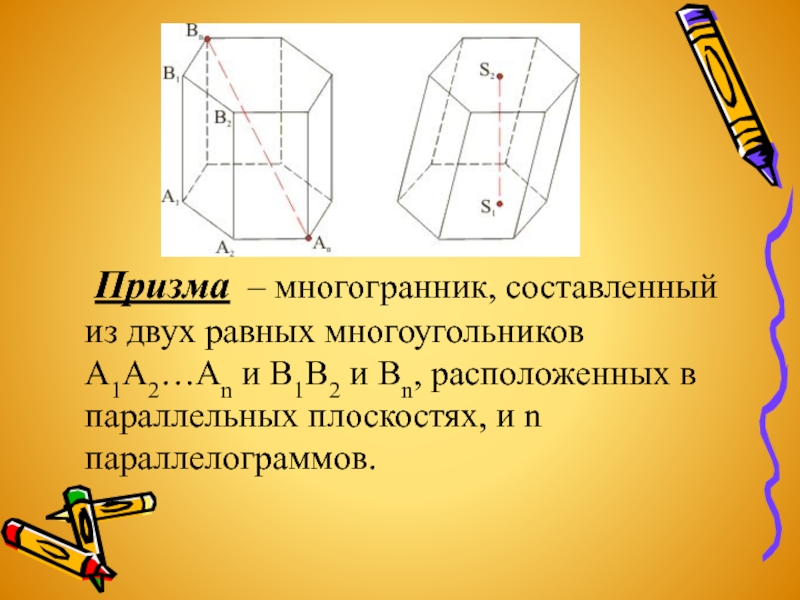
- 3. Призма – многогранник, составленный из двух равных
- 4. Если боковые ребра призмы перпендикулярны к основаниям,
- 5. Теорема: Объем прямой призмы равен произведению площади
- 6. Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом
- 7. Плоскость BB1D разделяет данную призму на 2
- 8. Теорема для произвольной прямой призмы с высотой
- 9. Задача № 1 Два ребра прямой четырехугольной
- 10. Слайд 10
- 11. РешениеПусть длина третьего ребра, исходящего из той
- 12. Задача №2 (Задание №11 ЕГЭ) Два
- 13. Решение: Длина диагонали параллелепипеда равна d =
- 14. Задача №3 ( Задание №11 ЕГЭ) Два
- 15. Задача №4 Дано: ABCA1B1C1- прямая призма.AB=BC=m; ABC= φ,BD- высота в ∆ ABC;BB1=BD.Найти: VABCA1B1C1-?
- 16. Решение:S ABC ·h, h=BB1.Рассмотрим ∆ ABC; ∆
- 17. Вопросы:Как найти объем прямой призмы?Основные шаги при доказательстве теоремы прямой призмы?
- 18. СПАСИБО ЗА ВНИМАНИЕ =)
Слайд 1Объем прямой призмы
МБОУ «Советская школа №2»
Презентацию подготовила
учитель 1 категории
Коржова
Слайд 2Цели урока:
Вспомнить понятие призмы.
Изучить теорему об объеме призмы.
Провести доказательство.
Применить полученные знания
Давайте уже начинать!
Слайд 3 Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2
Слайд 4Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой.
Прямая
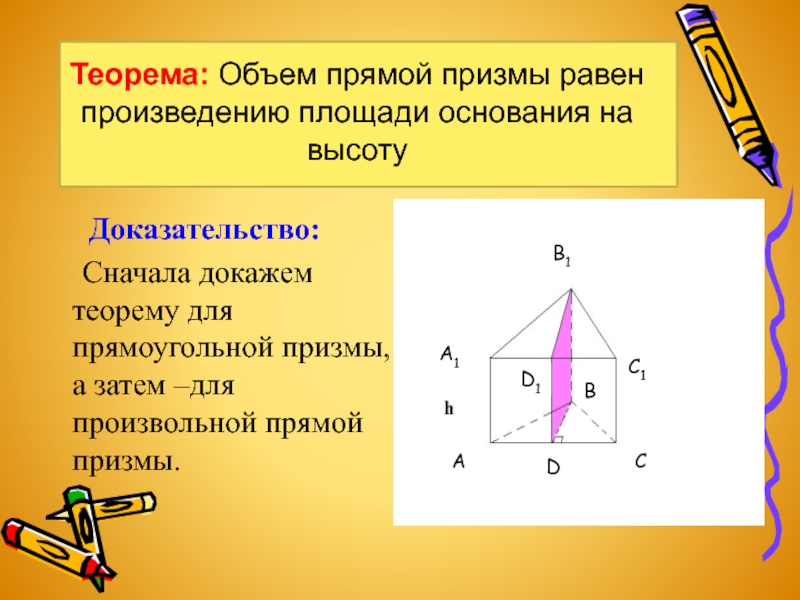
Слайд 5Теорема: Объем прямой призмы равен произведению площади основания на высоту
Сначала докажем теорему для прямоугольной призмы, а затем –для произвольной прямой призмы.
В
D1
А1
В1
С1
А
C
D
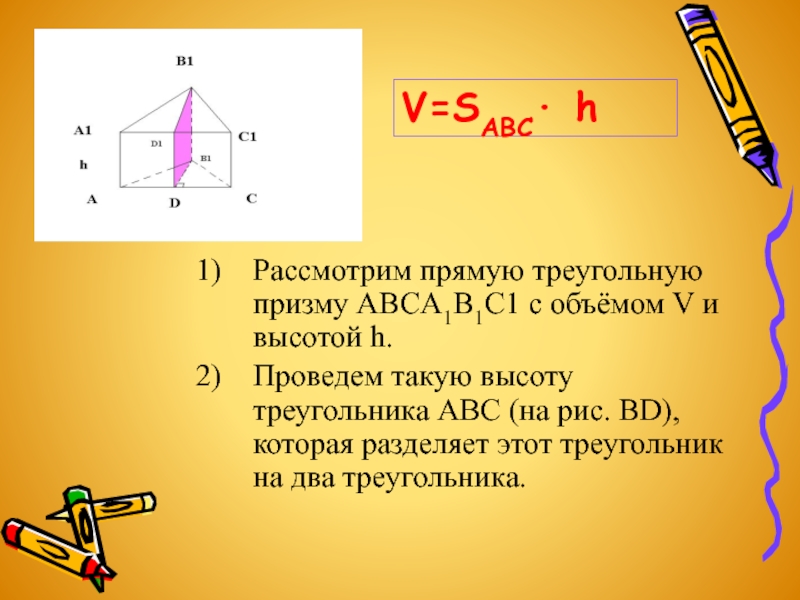
Слайд 6Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h.
Проведем
V=SABC∙ h
Слайд 7Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются
Поэтому объемы V1 и V2 этих призм соответственно равны
S ABD ·h и S BDC ·h.
По свойству 2 объемов
V=V1 +V2, т.е
V=SABD ·h=(SABD+SBDC) · h.
Таким образом, V= SABC ·h.
Слайд 8Теорема для произвольной прямой призмы с высотой h и площадью основания
Такую призму можно разбить на прямые треугольные призмы с высотой h. На рисунке изображена пятиугольная призма, которая разбита на три прямоугольные призмы.
Выразим объем каждой прямоугольной призмы по формуле V= SABC ·h и сложим эти объемы, вынесем за скобки общий множитель h, потом получим в скобках сумму площадей оснований треугольных призм, т.е. площадь S основания исходной призмы. Таким образом, объем исходной призмы равен произведению S · h.
Слайд 9Задача № 1
Два ребра прямой четырехугольной призмы , в основании
Слайд 11Решение
Пусть длина третьего ребра, исходящего из той же вершины, равна х, тогда
Длина диагонали прямоугольного параллелепипеда равна квадратному корню из суммы квадратов его измерений, поэтому d = = .
Находим объём по формуле V = a·b·c, следовательно V =
Ответ: ; куб. ед.
Слайд 12 Задача №2 (Задание №11 ЕГЭ) Два ребра правильной четырехугольной призмы, выходящие
Слайд 13Решение: Длина диагонали параллелепипеда равна d = Длина третьего ребра тогда х
Слайд 14Задача №3 ( Задание №11 ЕГЭ) Два ребра прямоугольного параллелепипеда, выходящие из
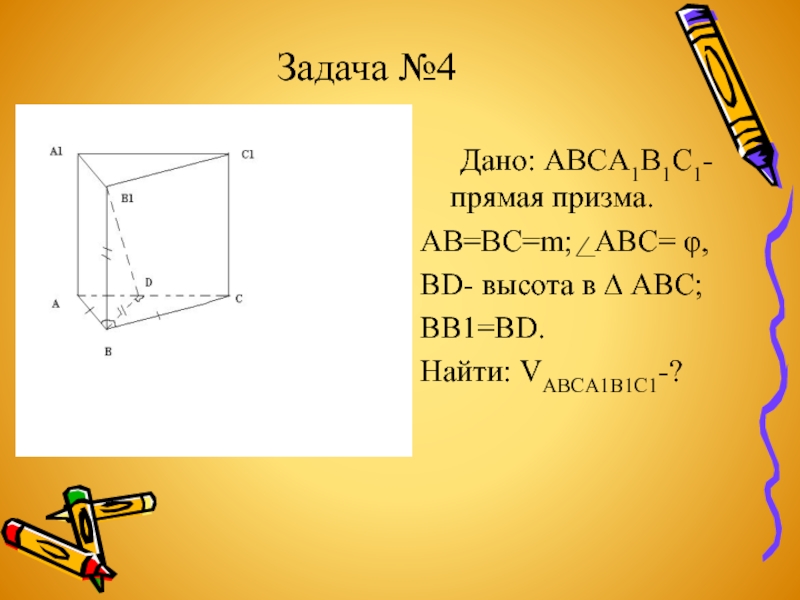
Слайд 15Задача №4
Дано: ABCA1B1C1- прямая призма.
AB=BC=m; ABC= φ,
BD- высота в ∆
BB1=BD.
Найти: VABCA1B1C1-?
Слайд 16Решение:
S ABC ·h, h=BB1.
Рассмотрим ∆ ABC; ∆ ABC- р/б. BD- высота
ABD= DBC= φ/2
3) Рассмотрим ∆ ABD; ∆ ABD- прямоугольный. Из соотношения в ∆: cosφ/2 = BD/AB BD= cosφ/2 AB, BD=m cosφ/2 (AB=m)
4) Т.к. BD=BB1 BB1=m · cos φ /2
5) S ABC= ½ AB·BC· sinφ; S ABC= ½ m2 · sinφ
6) V= ½ m2 · sinφ· mcosφ/2=½ m3 · sinφ · cosφ/2
Ответ: ½ m3 · sinφ · cosφ/2