- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по математикеТеорема Пифагора
Содержание
- 1. Презентация к уроку по математикеТеорема Пифагора
- 2. «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора…»
- 3. «Почему теорему Пифагора называют сокровищем геометрии?»Первая
- 4. Пифагорейцы занимались математикой, философией, естественными науками. Ими
- 5. Слайд 5
- 6. Слайд 6
- 7. Представление группы «Теоретики», их задачи:отыскать несколько способов
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
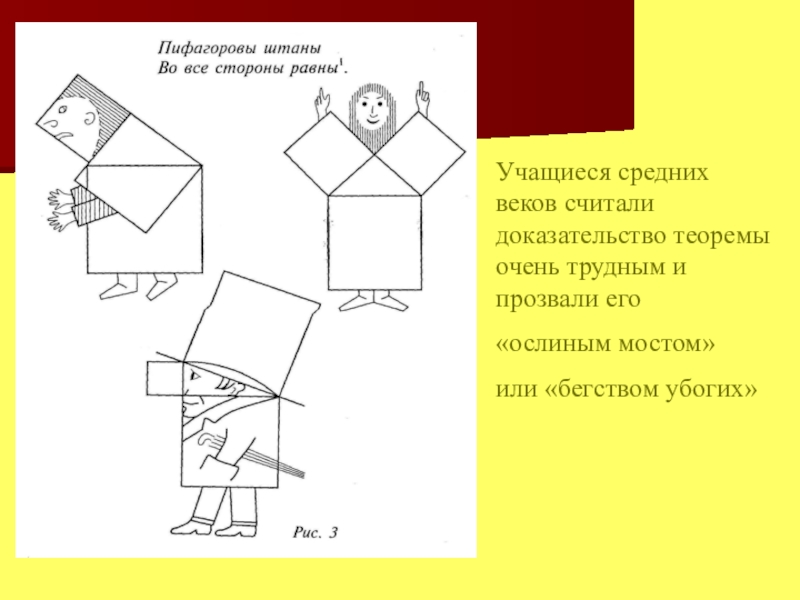
- 14. Учащиеся средних веков считали доказательство теоремы очень трудным и прозвали его «ослиным мостом» или «бегством убогих»
- 15. Если дан нам треугольник,И при том с
- 16. aсbТеорема Пифагора занимает в геометрии особое место.
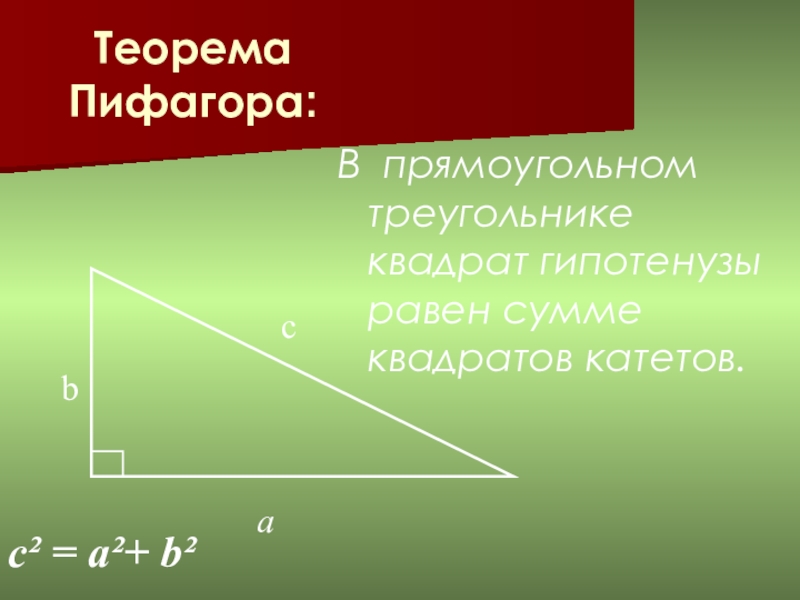
- 17. Теорема Пифагора:В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.bсаc² = a²+ b²
- 18. Задача из учебника «Арифметика» Леонтия Магницкого «Случися
- 19. Решение старинных задачЗадача индийского математика XII в.
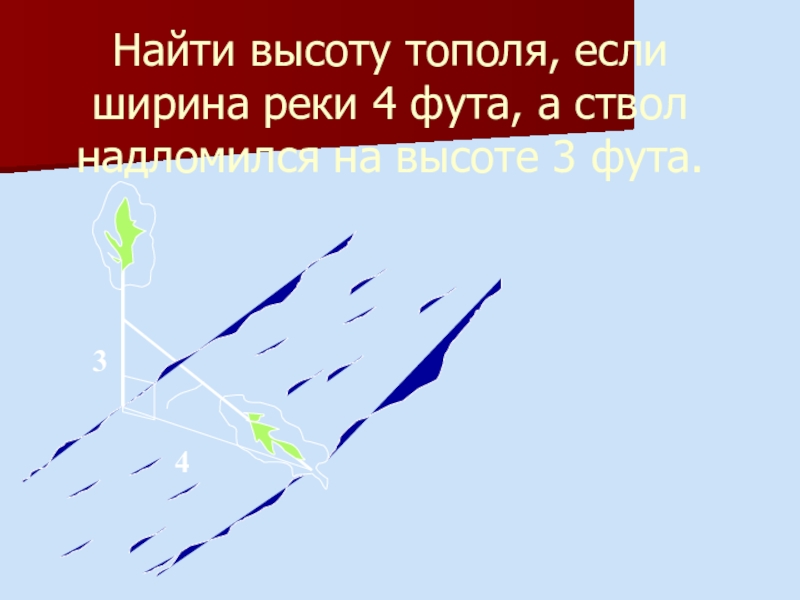
- 20. Найти высоту тополя, если ширина реки 4 фута, а ствол надломился на высоте 3 фута.34
- 21. Суть истины вся в том, что нам
- 22. Жил-был мудрец. К нему все шли
«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора…»
Слайд 3«Почему теорему Пифагора
называют сокровищем геометрии?»
Первая группа «Историки» ставит задачи:
изучить биографию
Пифагора;
изучить историю открытия теоремы;
установить какое значение имеет открытие теоремы Пифагора в геометрии;
сформулировать в чем заключается гениальность теоремы Пифагора.
изучить историю открытия теоремы;
установить какое значение имеет открытие теоремы Пифагора в геометрии;
сформулировать в чем заключается гениальность теоремы Пифагора.
Слайд 4
Пифагорейцы занимались математикой, философией, естественными науками. Ими были сделаны важные открытия
в арифметике и геометрии. В школе существовало правило, по которому авторство всех работ приписывалось Пифагору. Так что достоверно неизвестно, какие открытия принадлежат самому ученому.
Слайд 7Представление группы «Теоретики», их задачи:
отыскать несколько способов доказательства теоремы Пифагора;
провести классификацию
методов доказательства;
привести примеры;
произвести синтез материалов и создать презентацию.
привести примеры;
произвести синтез материалов и создать презентацию.
Слайд 14
Учащиеся средних веков считали доказательство теоремы очень трудным и прозвали его
«ослиным мостом»
или «бегством убогих»
Слайд 15
Если дан нам треугольник,
И при том с прямым углом,
То квадрат гипотенузы
Мы
всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путем
К результату мы придем.
Слайд 16
a
с
b
Теорема Пифагора занимает в геометрии особое место. На основе теоремы можно
вывести или доказать большинство теорем. А еще она замечательна тем, что сама по себе вовсе не очевидна. Сколько ни смотри на прямоугольный треугольник, никак не увидишь, что его стороны а, b и с связывает простое соотношение:
c² = a²+ b²
c² = a²+ b²
Слайд 17Теорема
Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
b
с
а
c² =
a²+ b²
Слайд 18
Задача из учебника «Арифметика» Леонтия Магницкого
«Случися некому человеку к стене
лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».
Слайд 19Решение старинных задач
Задача индийского математика XII в. Бхаскары.
На берегу реки рос
тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута всего широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута всего широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Слайд 21
Суть истины вся в том,
что нам она – навечно,
Когда хоть
раз в прозрении её увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна …
(А. Шамиссо)
(А. Шамиссо)
Слайд 22
Жил-был мудрец. К нему все шли за советами, его все
уважали. Но среди всех был один завистник. Он сказал, что мудрец не такой уж умный, и он может это доказать. «Я задам вопрос, на который он не сможет ответить. Я поймаю бабочку, зажму ее в руках и спрошу – какая бабочка у меня в руках: живая или неживая. Если он скажет «неживая», я выпущу её. Если он скажет «живая», я ее задавлю, и он будет неправ». Завистник на глазах у толпы подошел к мудрецу с зажатой в руках бабочкой и спросил: «Отгадай, что у меня здесь: живое или неживое?» И мудрец ответил:
«Все в твоих руках!»