- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по математике Теорема Пифагора
Содержание
- 1. Презентация к уроку по математике Теорема Пифагора
- 2. Теорема Пифагора "Пифагоровы штаны Во все стороны равны" (Исторический экскурс)
- 3. «Теорема Пифагора» «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом».Анатоль Франс.
- 4. Цели урока: познакомиться с теоремой Пифагора; научиться применять эту теорему при решении задач.
- 5. Лаборатория – специальное помещение для научных исследований.
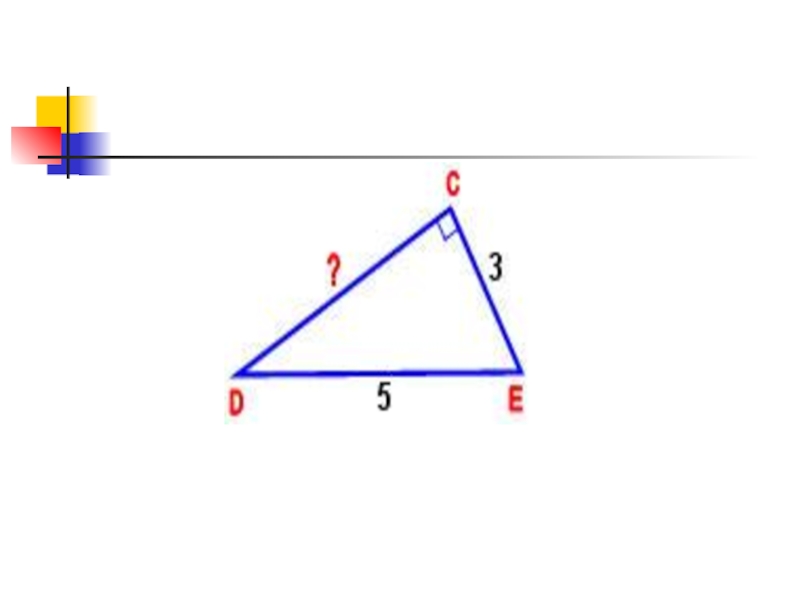
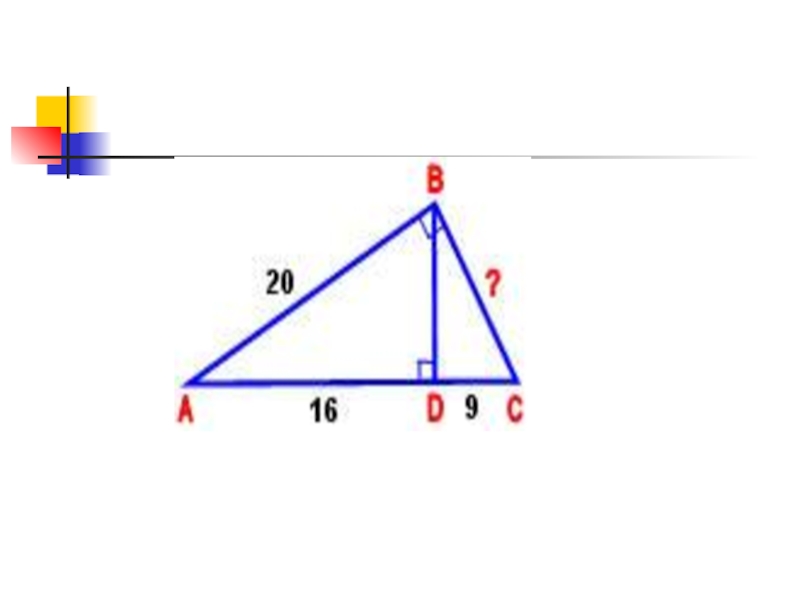
- 6. «Испытания».Устная работа.1 – испытание:Перед вами треугольники:
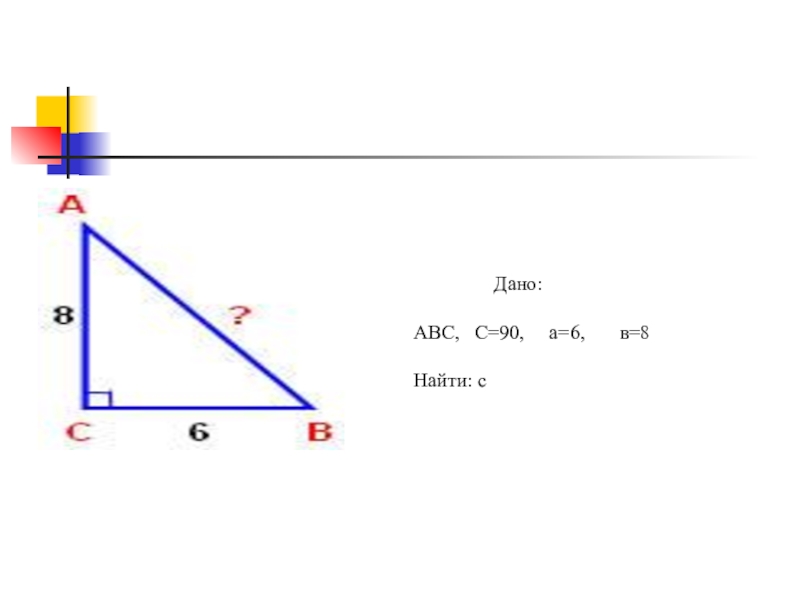
- 7. 2 – испытание:Чему равно 5^2; 7^2;
- 8. Лаборатория науки.
- 9. Слайд 9
- 10. Без преувеличения можно сказать, что это самая
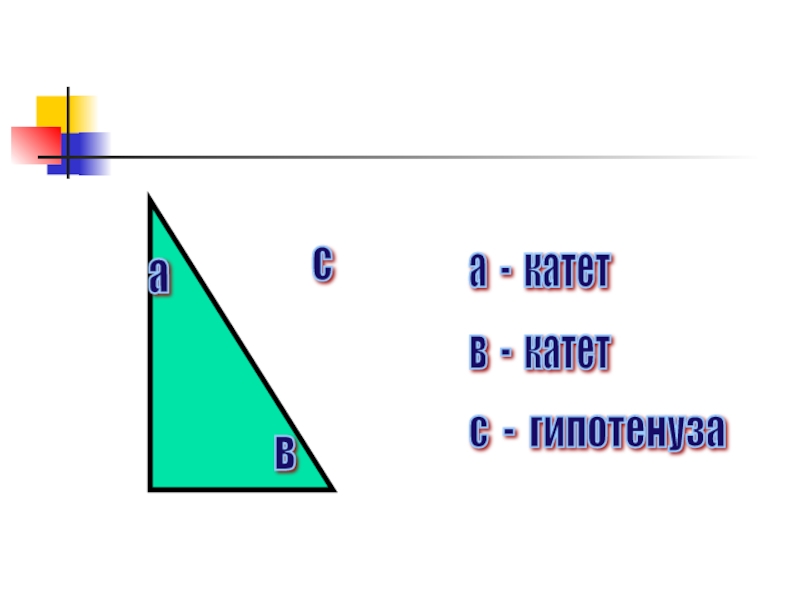
- 11. а в с
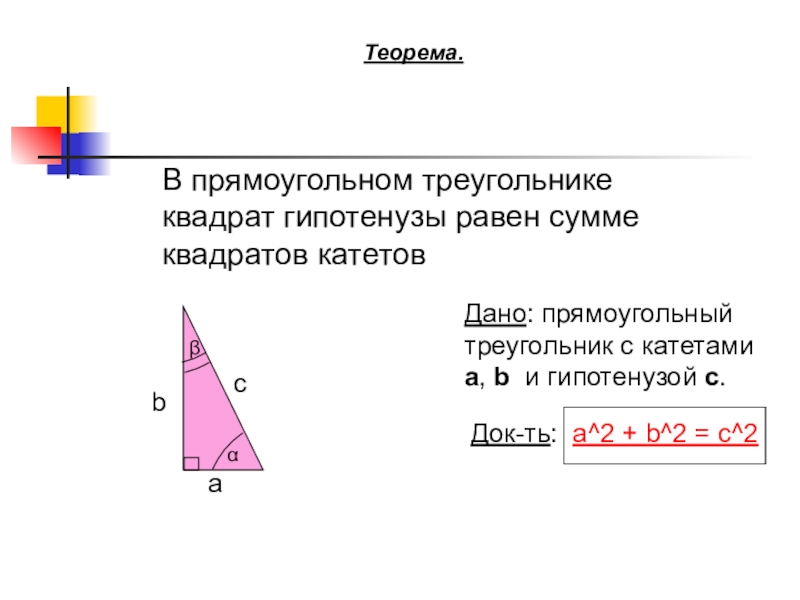
- 12. Теорема.В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 13. Доказательство:Достроим данный треугольник до квадрата со стороной
- 14. И. ДырченкоЕсли дан нам треугольникИ притом с
- 15. «В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 16. Доказательство теоремы считалось в кругах учащихся средних
- 17. Лаборатория интересных фактов.
- 18. Пифагор – древнегреческийПифагор – древнегреческий ученый (VIVI
- 19. Великий ученый Пифагор Родился около
- 20. Пифагорейское братствоВ возрасте 40 лет Пифагор покидает
- 21. Симметрия жизни
- 22. Пифагореизм у истоков научного знания.Школа Пифагора состояла
- 23. Теорема ПифагораУ Пифагора много открытий, но наиболее
- 24. К теореме Пифагора его ученики составляли
- 25. Теорему называли «мостом ослов», так как слабые
- 26. Лаборатория знаний.
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Домашнее задание: п.п.14,15, доказательство теоремы, №92, 97.
- 31. Притча – малый литературный жанр,
- 32. Шёл мудрец, а навстречу ему
- 33. «Геометрия является самым могущественным средством для
- 34. Источники информации:www.1september.ru/ruhttp://root/И. Глейзер. История математики в школе.//images.yandex.ru/yandsearch?А.Д.Александров
Слайд 1Урок - презентация
«Теорема Пифагора»
8 класс
МКОУ СОШ с. Црау
Царукаева
учитель математики
Слайд 3
«Теорема Пифагора»
«Учиться можно только весело… Чтобы переваривать знания, надо поглощать их
Анатоль Франс.
Слайд 4Цели урока:
познакомиться с теоремой Пифагора;
научиться применять эту теорему при
Слайд 10Без преувеличения можно сказать, что это самая известная теорема геометрии, ибо
Теорема Пифагора!
Слайд 12
Теорема.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Дано: прямоугольный
треугольник с
Док-ть: a^2 + b^2 = c^2
Слайд 13Доказательство:
Достроим данный треугольник до квадрата со стороной (a + b) так,
Sкв. = (a + b)^2 или Sкв. = 4Sтр. + S`кв.
Sтр. = 1/2ab; S`кв. = c^2, тогда
Sкв. = 4 *1/2ab + c^2
Т.о., (a + b)^2 = 4 *1/2ab + c^2
a^2 + 2ab + b^2 = 2ab + c^2
a^2 + b^2 = c^2
Слайд 14И. Дырченко
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы
Катеты в квадрат возводим,
Сумму степеней находим —
И таким простым путем
К результату мы придем.
Слайд 15
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетовкатетов».
Формулировки
Во времена Пифагора формулировка теоремы звучала так:
Слайд 16
Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и
Сейчас известно около 150 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.)
“Dons asinorum” -
«ослиный мост»
или
“elefuga” -
«бегство убогих»
«ветряной мельницей»,
«теоремой – бабочкой»
или
«теоремой невесты»
а сама теорема –
Слайд 18Пифагор – древнегреческийПифагор – древнегреческий ученый (VIVI в. до н.э.)
Слайд 19Великий ученый Пифагор
Родился около 570 г. до н.э.
Отцом Пифагора был Мнесарх, резчик по драго-ценным камням.
Имя же матери не сохранилось. Некоторые называли ее Пифайдой, дочерью основателя Самоса .
Учителями были: Гермодамант и Ферекид Сиросский
В Милете встречается с Фалесом.
В 548 г. до н.э. он отправился в Египет.(ему20 лет)
Через 11 лет , возвращаясь домой попал в плен к царю Вавилона.
В 530 г. до н.э он вернулся на родину.
В 40 лет переезжает в Кротон .
Жена Милона Мия, сын и дочь.
...Прошло 20 лет, 510 г. умирает
Слайд 20Пифагорейское братство
В возрасте 40 лет Пифагор покидает Самос и переезжает в
В Кротоне он учредил братство или союз. Он был и политическим клубом, и научным обществом – центром духовной и общественной жизни полиса.
Кодекс пифагорейцев – «Золотые стихи»
Сыщи себе верного друга; имея его, ты можешь обойтись без богов.
Юноша! Если ты желаешь себе жизни долгоденственной, то воздержи себя от пресыщения и всякого излишества.
Юные девицы! Помятуйте, что лицо лишь тогда бывает прекрасным, когда оно изображает изящную душу.
Не гоняйтесь за счастьем: оно всегда находится в тебе самом.
Не пекись о снискании великого знания: из всех знаний нравственная наука, быть может, есть самая нужнейшая, но ей не обучаются.
Символом или опознавательным знаком пифагорейцев была пентаграмма или пифагорейская звезда.
Слайд 22Пифагореизм у истоков научного знания.
Школа Пифагора состояла из двух ступеней: одних
Пифагорейская система знаний ( математе) состояла из четырех разделов: арифметики (наука о числе), геометрии (учение о фигурах и их измерении), музыки (учение о гармонии или теории музыки), астрономии (учение о строении Вселенной).
Арифметика: натуральные числа, фигурные, простые, четные и нечетные числа. Учение о правилах действий над числами – логистика. ( действия с натуральными числами, извлечение корня квадратного, кубического, действия с дробями, вычисления на счетной доске). Нумерация с помощью 27 букв гр. Алфавита. Таблица Пифагора. Учение о пропорциях. Пифагорейцы знали три вида пропорций: арифметическую, геометрическую, гармоническую. Несоизмеримость чисел. «Все есть число»
Музыка. Сам Пифагор обнаружил, что приятные слуху созвучия – консанансы получаются в том случае, когда длина струн относятся как целые числа первой четверки, т.е. 1:2, 2:3, 3:4. Это открытие потрясло его. Ведь столь эфемерное явление, как звук . Поддавалось числовой характеристике.
Астрономия. Звездное небо всегда будоражило умы человечества и разум пифагорейцев в том числе. Они верили в гармоническое устройство мироздания , впервые назвали вселенную космосом (строй, порядок). Пифагорейцы утверждали, что траектории планет – окружности, а их форма шарообразна. Модель устройства вселенной. Утренняя и вечерняя звезда – это одна звезда: Венера.
Геометрия. Впервые геометрию стали изучать как науку о свойствах абстрактных фигур. «Предания Пифагора»- первый учебник по геометрии. Пифагорейцы проявляли повышенный интерес к правильным фигурам и телам. Систематическое введение доказательств. Основные истины (основные фигуры и положения – аксиомы) Теорема о сумме углов треугольника. Теорема Пифагора
Слайд 23Теорема Пифагора
У Пифагора много открытий, но наиболее популярна теорема, которая носит
Эта теорема была известна еще в 2000г.до н.э.
- В египетском папирусе :египетский треугольник (правило веревки)
- в Вавилонских клинописях
- В китайском трактате
- В древнеиндийском (правило веревки)
Пифагор дал первое доказательство этой теоремы.
С ней связано много легенд.
Слайд 24 К теореме Пифагора его ученики составляли стишки, вроде:
«Пифагоровы штаны
во все
А также рисовали такие карикатуры:
Шарж из учебника XVI века.
Слайд 25Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть,
Или «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.
"asses bridge"
"squalid"
Слайд 32 Шёл мудрец, а навстречу ему три человека, которые везли
Ребята! Давайте и мы попробуем с вами оценить каждый свою работу за урок.
Кто работал так, как первый человек? Поднимите синие треугольники.
Кто работал добросовестно? Поднимите зеленые треугольники.
Кто принимал участие в строительстве храма? Поднимите красные треугольники.
Слайд 33
«Геометрия является самым могущественным средством для изощрения наших умственных способностей
Галилео Галилей
Спасибо за урок!
Слайд 34Источники информации:
www.1september.ru/ru
http://root/
И. Глейзер. История математики в школе.
//images.yandex.ru/yandsearch?
А.Д.Александров и др. Геометрия 7-9
Атанасян
В.Н.Руденко, Г.А.Бахурин Геометрия 7-9
В.Д.Чистяков. Старинные задачи по элементарной математике