вписанный угол»
Учитель математики
МКОУ «Колпаковская СОШ» Ежова Л.М.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по математике 8 класс по теме: Окружность вписанная и описанная п
Содержание
- 1. Презентация к уроку по математике 8 класс по теме: Окружность вписанная и описанная п
- 2. Слайд 2
- 3. Окружность
- 4. Содержание :Взаимное расположение прямой и окружностиУглы, связанные
- 5. Углы, связанные с окружностью. оАВАВСУгол АОВ –…...
- 6. Свойства вписанных углов.Вписанные углы, опирающиеся на одну
- 7. Свойство отрезков касательных.АВОКасательная к окружности ….. к
- 8. Свойства отрезков хорд, секущих и касательных.Отрезки пересекающихся
- 9. Вписанная окружность. В…….. треугольник можно вписать окружность.
- 10. Вписанная окружность8В любом описанном четырехугольнике суммы противоположных
- 11. Слайд 11
- 12. Это забавноМаленькие и плотно прилегающие ушки вписываются в окружность головы!
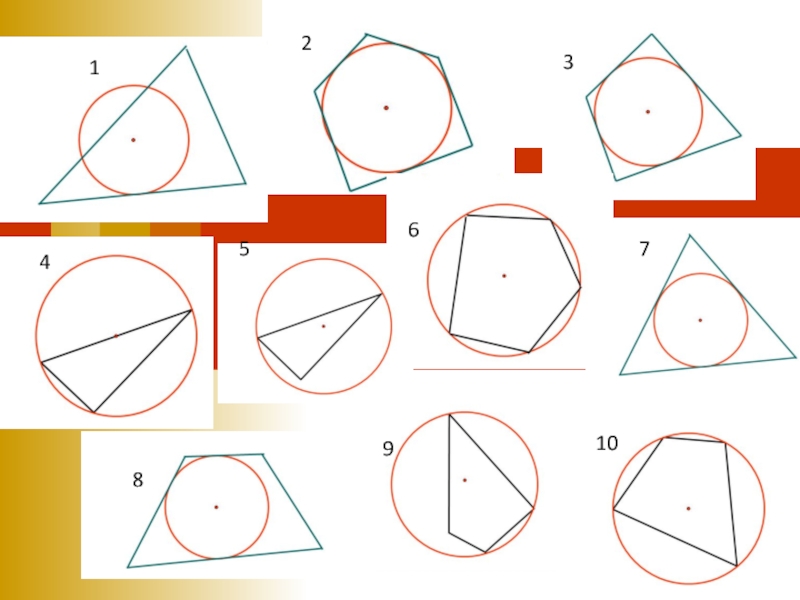
- 13. 12345678910
- 14. Вид текста, вписанного в окружность!Можно ли Описать окружность около треугольника?
- 15. Решить задачу.Три соседа мужика (Фёдор, Яков и
- 16. Задачи:1.Найти точку, равноудалённую от вершин треугольника2.Выяснить, какой
- 17. Около ……треугольника можно….
- 18. Задание 1.- кроссворд по теме «Окружность»( заполнить)-
- 19. Около любого ли треугольника можно описать окружность?Задание
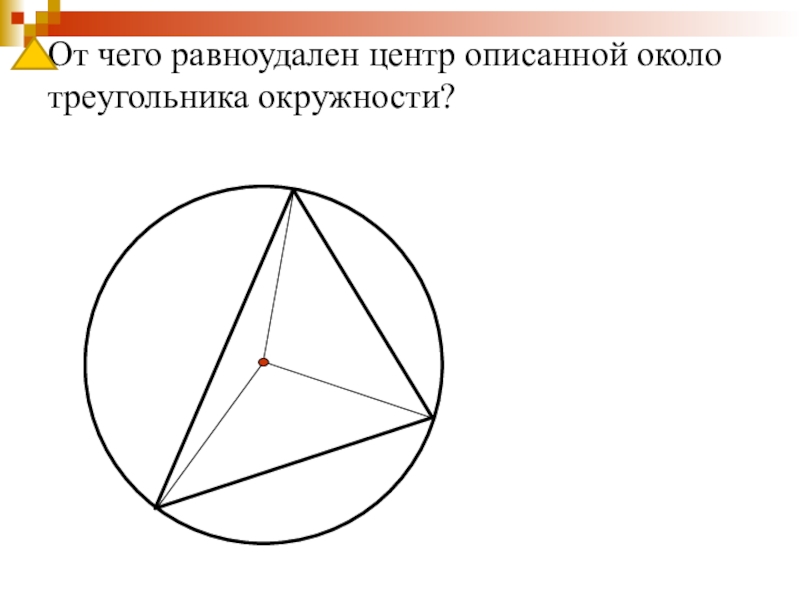
- 20. От чего равноудален центр описанной около треугольника окружности?
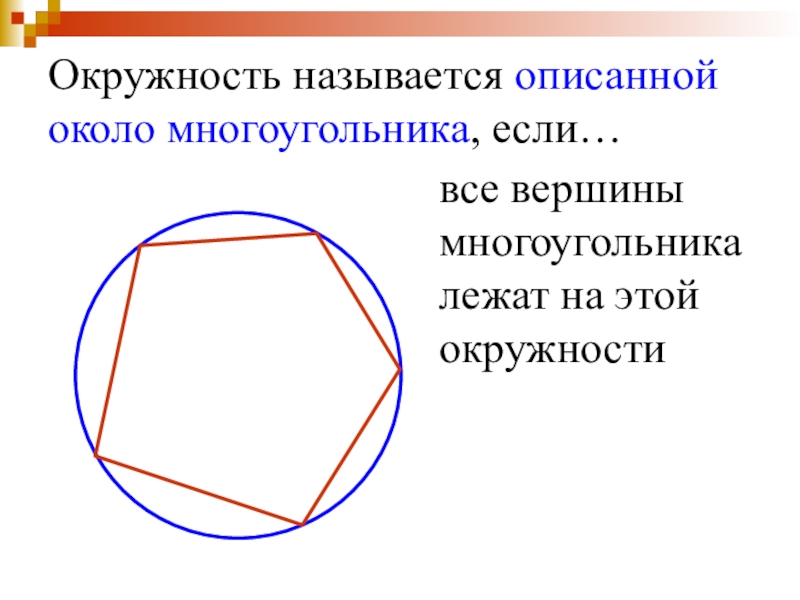
- 21. Окружность называется описанной около многоугольника, если…все вершины многоугольника лежат на этой окружности
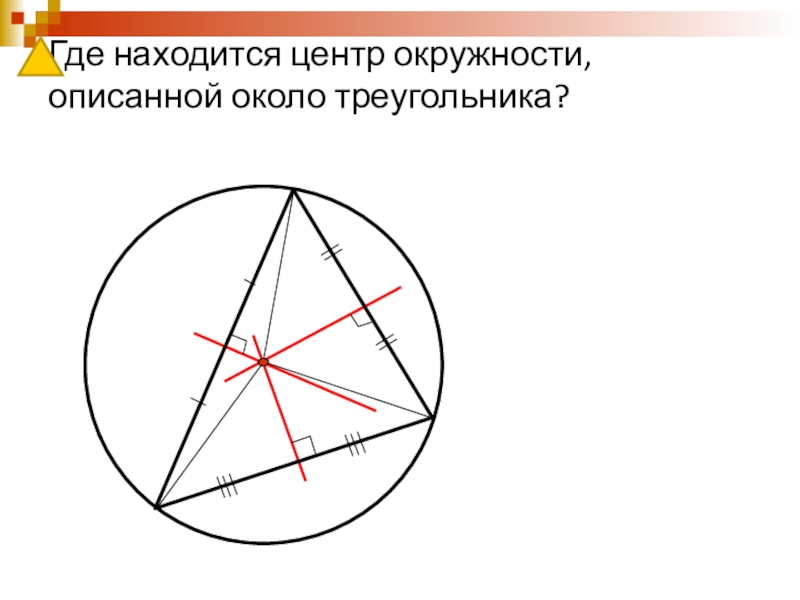
- 22. Где находится центр окружности, описанной около треугольника?
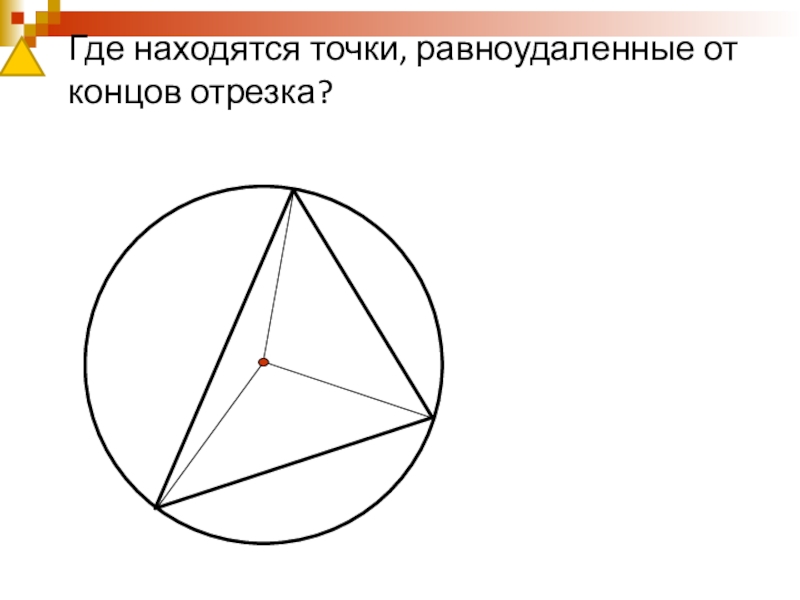
- 23. Где находятся точки, равноудаленные от концов отрезка?
- 24. Окружность называется описанной около многоугольника, если…все вершины многоугольника лежат на этой окружности
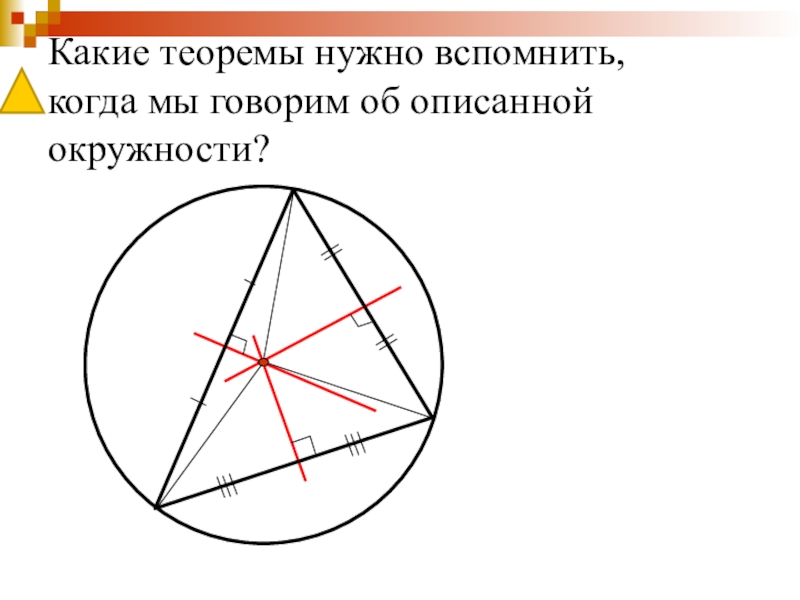
- 25. Какие теоремы нужно вспомнить, когда мы говорим об описанной окружности?
- 26. Теорема об окружности описанной около треугольникаТеорема: Около любого треугольника можно описать окружность
- 27. Около любого ли четырёхугольника можно описать окружность?Задание
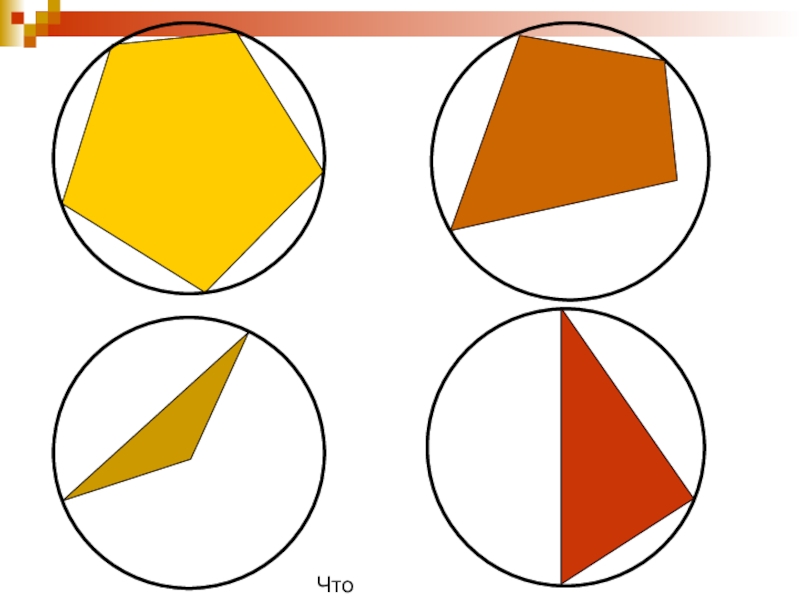
- 28. Что лишнее?
- 29. Успехов в изучении данной темы ! Задача
- 30. № 702АВСАВ-диаметр͜ВС=134⁰Дано:Найти углы ∆ АВС
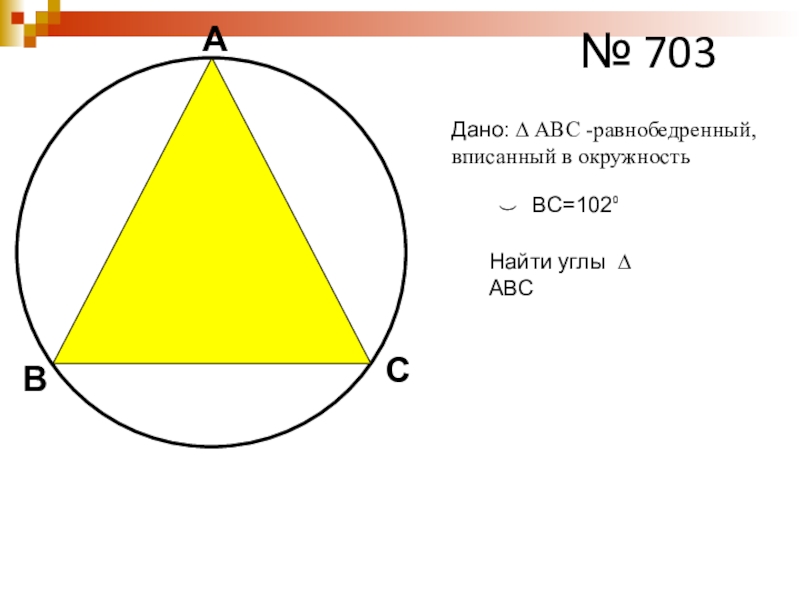
- 31. АВС№ 703͜ВС=102⁰ Дано: ∆ АВС -равнобедренный, вписанный в окружностьНайти углы ∆ АВС
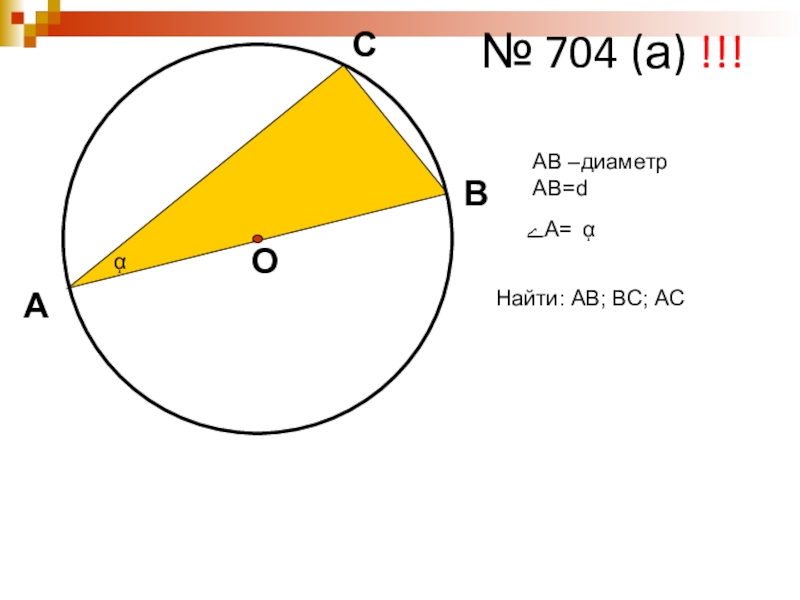
- 32. АВСО№ 704 (а) !!!ᾳАВ –диаметрАВ=dےА=ᾳНайти: АВ; ВС; АС
- 33. Задача № 1Задача: Четырехугольник АВСD вписан в
- 34. Жили в городе Геометрии Треугольник и Окружность.
- 35. Домашнее задание:П.75, №704(б),
- 36. Слайд 36
- 37. Спасибо за урок
- 38. Использованные источники:Учебник: Геометрия, 7-9 классы, Л.С.Атанасян, В.Ф.Бутузов,
Окружность
Слайд 4Содержание :
Взаимное расположение прямой и окружности
Углы, связанные с окружностью.
Свойства вписанных углов.
Свойства
отрезков хорд, секущих и касательных .
Вписанная и описанная окружность
Тест.
Вписанная и описанная окружность
Тест.
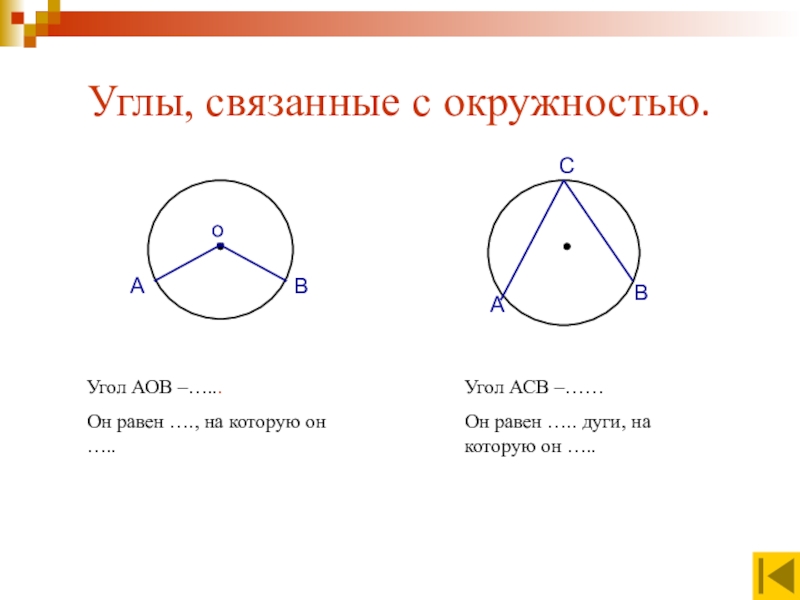
Слайд 5Углы, связанные с окружностью.
о
А
В
А
В
С
Угол АОВ –…...
Он равен …., на
которую он …..
Угол АСВ –……
Он равен ….. дуги, на которую он …..
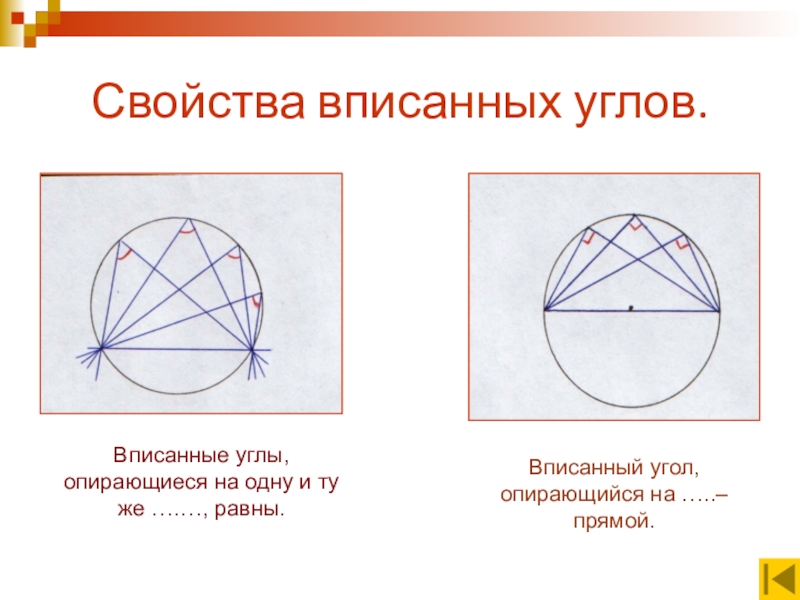
Слайд 6Свойства вписанных углов.
Вписанные углы, опирающиеся на одну и ту же ….…,
равны.
Вписанный угол, опирающийся на …..– прямой.
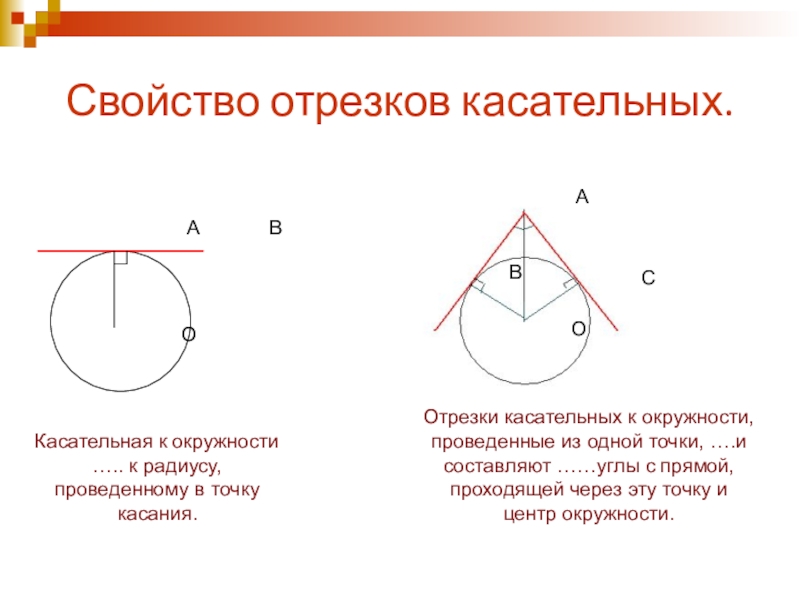
Слайд 7Свойство отрезков касательных.
А
В
О
Касательная к окружности ….. к радиусу, проведенному в точку
касания.
А
О
С
В
Отрезки касательных к окружности, проведенные из одной точки, ….и составляют ……углы с прямой, проходящей через эту точку и центр окружности.
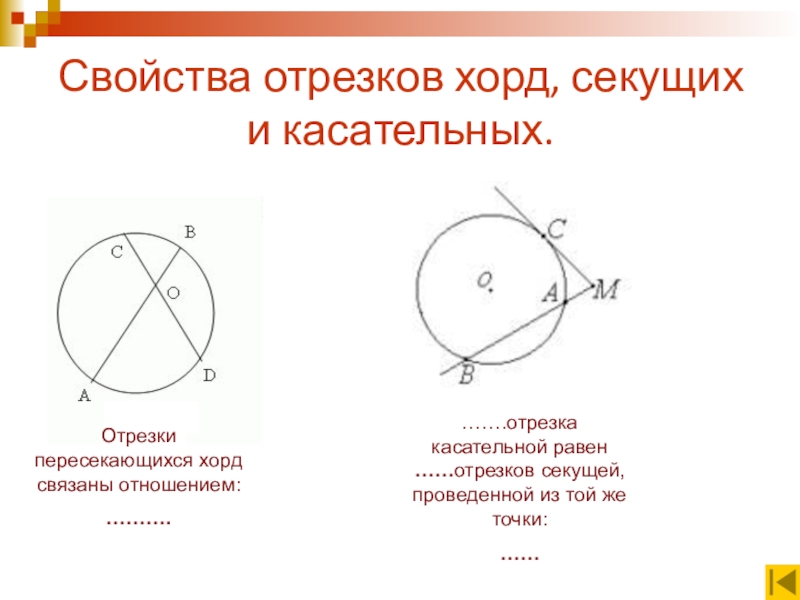
Слайд 8Свойства отрезков хорд, секущих и касательных.
Отрезки пересекающихся хорд связаны отношением:
……….
…….отрезка касательной
равен ……отрезков секущей, проведенной из той же точки:
……
……
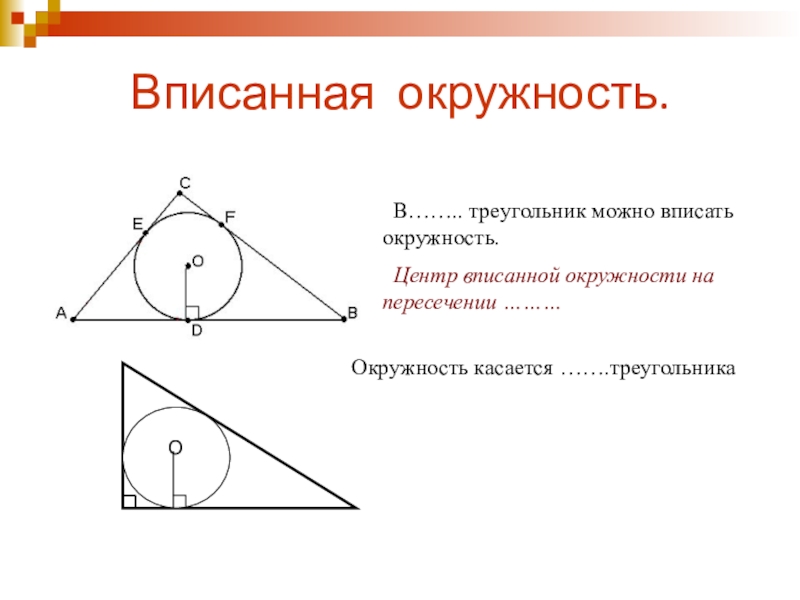
Слайд 9Вписанная окружность.
В…….. треугольник можно вписать окружность.
Центр вписанной окружности на
пересечении ………
О
Окружность касается …….треугольника
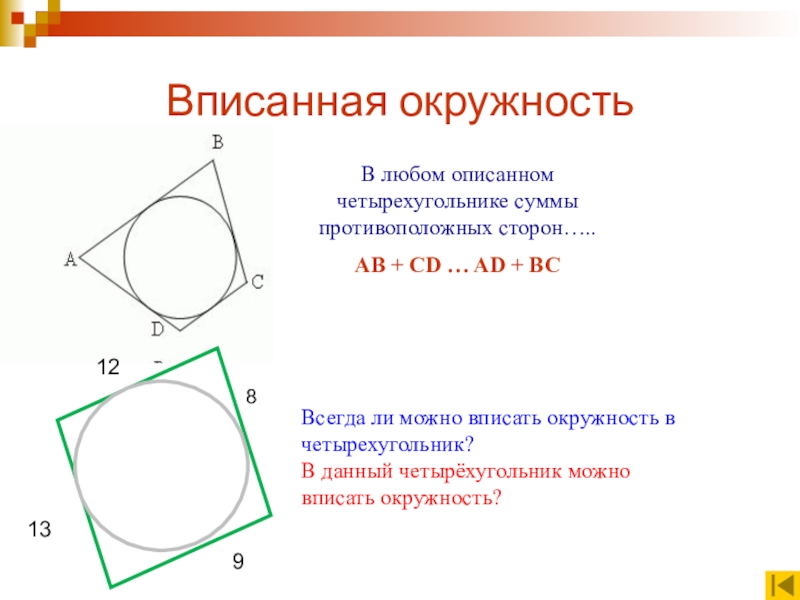
Слайд 10Вписанная окружность
8
В любом описанном четырехугольнике суммы противоположных сторон…..
АВ + CD …
AD + BC
Всегда ли можно вписать окружность в четырехугольник?
В данный четырёхугольник можно вписать окружность?
12
9
13
Слайд 11 Это интересно
Центр окружности, которую
описывает радуга, всегда лежит на прямой, проходящей через Солнце и глаз наблюдателя!
Слайд 15Решить задачу.
Три соседа мужика (Фёдор, Яков и Лука
Чтоб всегда с
водою жить
Стали свой колодец рыть
Но Лука вдруг говорит:
«Ведь момент один забыт!
Нужно длины всех дорог
От колодца на порог
Сделать равными, друзья!
Допускать обит нельзя!»
И смекни путём каким?
Стали свой колодец рыть
Но Лука вдруг говорит:
«Ведь момент один забыт!
Нужно длины всех дорог
От колодца на порог
Сделать равными, друзья!
Допускать обит нельзя!»
И смекни путём каким?
Слайд 16Задачи:
1.Найти точку, равноудалённую от вершин треугольника
2.Выяснить, какой фигуре принадлежат точки?
3. Рассмотреть
определение окружности, описанной около треугольника
4. Выявить, около любого ли четырёхугольника можно описать окружность?
4. Выявить, около любого ли четырёхугольника можно описать окружность?
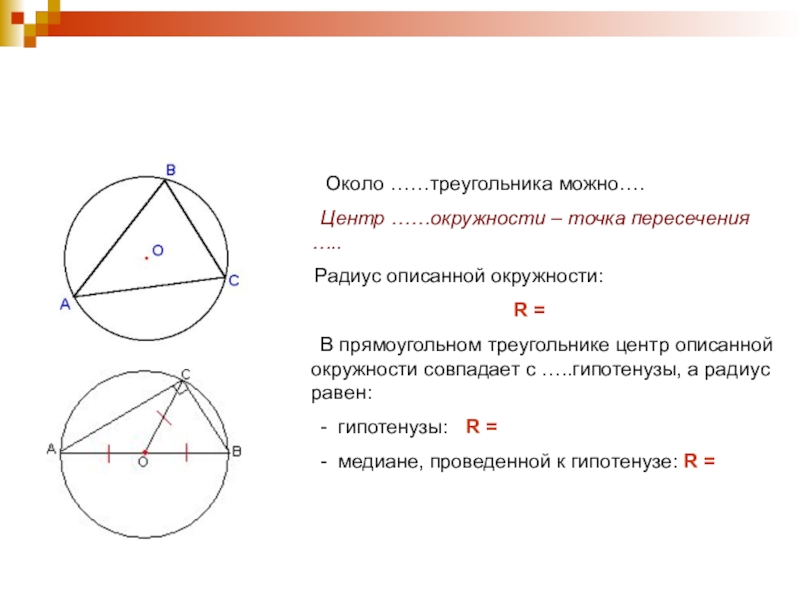
Слайд 17 Около ……треугольника можно….
Центр
……окружности – точка пересечения …..
Радиус описанной окружности:
R =
В прямоугольном треугольнике центр описанной окружности совпадает с …..гипотенузы, а радиус равен:
- гипотенузы: R =
- медиане, проведенной к гипотенузе: R =
Радиус описанной окружности:
R =
В прямоугольном треугольнике центр описанной окружности совпадает с …..гипотенузы, а радиус равен:
- гипотенузы: R =
- медиане, проведенной к гипотенузе: R =
Слайд 18Задание 1.
- кроссворд по теме «Окружность»( заполнить)
- Найти ошибку в определении:
Окружность называется описанной около многоугольника, если она соединяет все его вершины.
- Дать определение окружности, описанной около многоугольника, используя учебник
Слайд 19Около любого ли треугольника можно описать окружность?
Задание 2: доказать это предположение.
Предположение-
теорема:……
- подсказка: наводящие вопросы с соответствующими рисунками
подсказка-план доказательства
Разобраться с доказательством в учебнике на стр.176
Слайд 21Окружность называется описанной около многоугольника, если…
все вершины многоугольника лежат на этой
окружности
Слайд 24Окружность называется описанной около многоугольника, если…
все вершины многоугольника лежат на этой
окружности
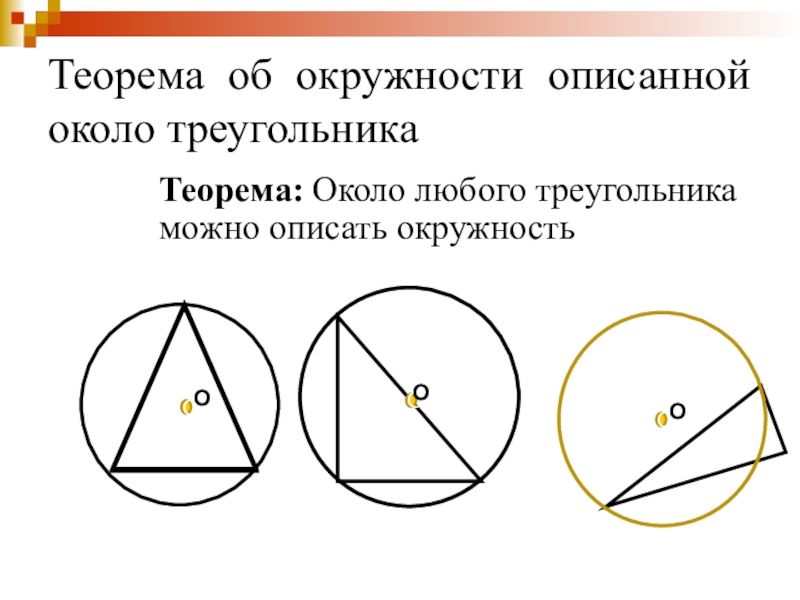
Слайд 26Теорема об окружности описанной около треугольника
Теорема: Около любого треугольника можно описать
окружность
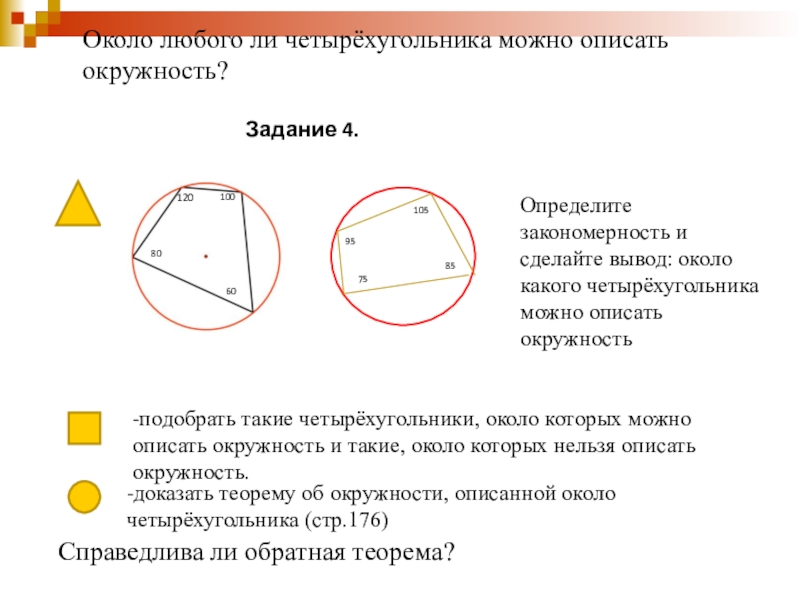
Слайд 27Около любого ли четырёхугольника можно описать окружность?
Задание 4.
-подобрать такие четырёхугольники, около
которых можно описать окружность и такие, около которых нельзя описать окружность.
-
120
100
80
60
105
75
95
85
Определите закономерность и сделайте вывод: около какого четырёхугольника можно описать окружность
-доказать теорему об окружности, описанной около четырёхугольника (стр.176)
Справедлива ли обратная теорема?
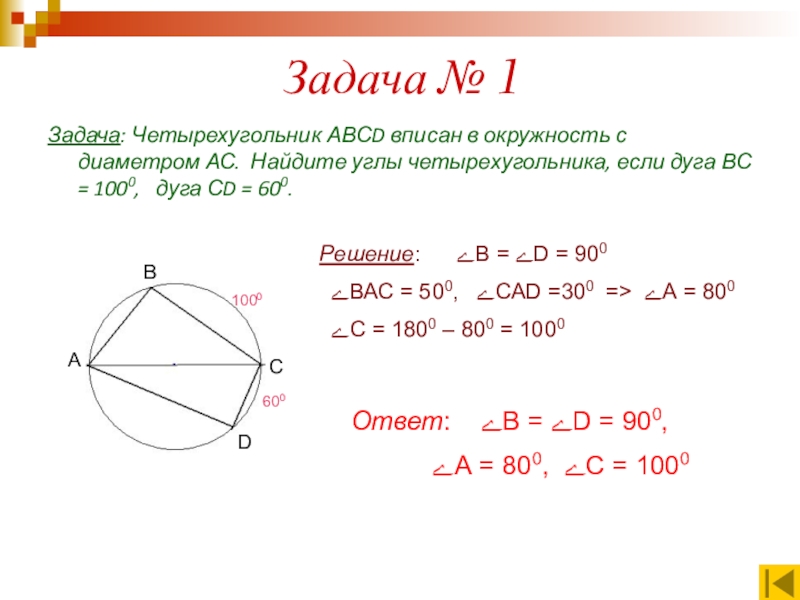
Слайд 33Задача № 1
Задача: Четырехугольник АВСD вписан в окружность с диаметром АС.
Найдите углы четырехугольника, если дуга ВС = 1000, дуга СD = 600.
А
В
С
D
Решение: ےВ = ےD = 900
ےВАС = 500, ےСАD =300 => ےА = 800
ےС = 1800 – 800 = 1000
1000
600
Ответ: ےВ = ےD = 900,
ےА = 800, ےС = 1000
Слайд 34Жили в городе Геометрии Треугольник и Окружность. Треугольник был логичен, разумен,
надёжен, в силу своей конструкции, но очень добр. Он спешил на помощь всем, кто в ней нуждался. Окружность была эмоциональна. Она любила весь мир и хотела, как можно больше вместить в себя, хотя где-то в глубине души, она считала себя ничтожно малой точкой, не имеющей никакой ценности во Вселенной.
Сказки об окружности
У нашей Окружности было образное мышление и богатое воображение. Тотчас же перед её глазами появилась картинка:
Слайд 35Домашнее задание:
П.75, №704(б),
№706(б).
Творческое задание :
Сочинить сказку
по данной теме или найти что-нибудь из рубрики: « ЭТО ИНТЕРЕСНО
или ЭТО ЗАБАВНО».
Можно ли решить проблему с колодцем, если мужчин будет 4 человека?
или ЭТО ЗАБАВНО».
Можно ли решить проблему с колодцем, если мужчин будет 4 человека?
Слайд 38Использованные источники:
Учебник: Геометрия, 7-9 классы, Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. М.:
Просвещение, 2009.
Н.Ф.Гаврилова, Поурочные разработки по геометрии: 8 класс. – М.: ВАКО, 2005 – (В помощь школьному учителю).
Для создания шаблона презентации использовались картинки https://yandex.ru/images/search?text=Для создания шаблона презентации использовались картинки https://yandex.ru/images/search?text=математика
Н.Ф.Гаврилова, Поурочные разработки по геометрии: 8 класс. – М.: ВАКО, 2005 – (В помощь школьному учителю).
Для создания шаблона презентации использовались картинки https://yandex.ru/images/search?text=Для создания шаблона презентации использовались картинки https://yandex.ru/images/search?text=математика
