- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по дисциплине Математика по теме Площадь криволинейной трапеции
Содержание
- 1. Презентация к уроку по дисциплине Математика по теме Площадь криволинейной трапеции
- 2. Повторяем термины23167541.Зависимость переменной Y от переменной x,
- 3. Найти пару: функция - первообразная
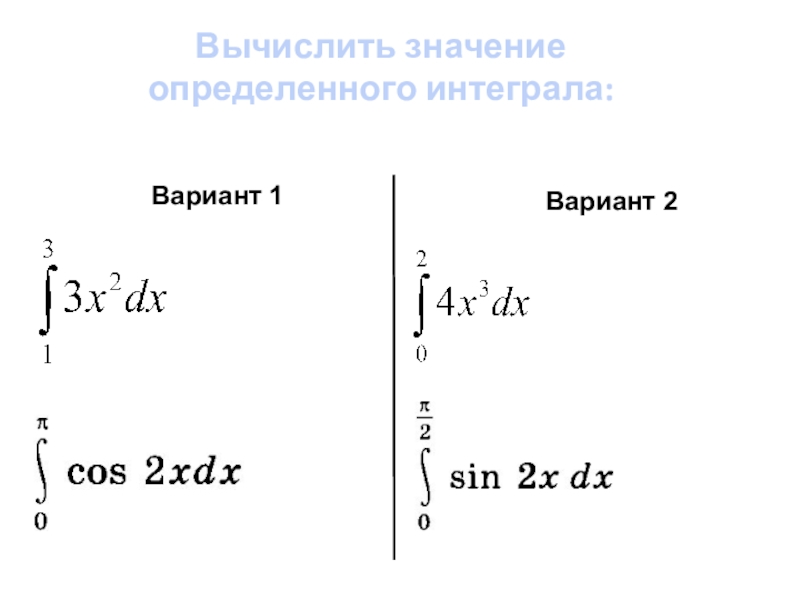
- 4. Вычислить значение определенного интеграла: Вариант 1Вариант 2
- 5. Тема урока: Площадь криволинейной трапеции
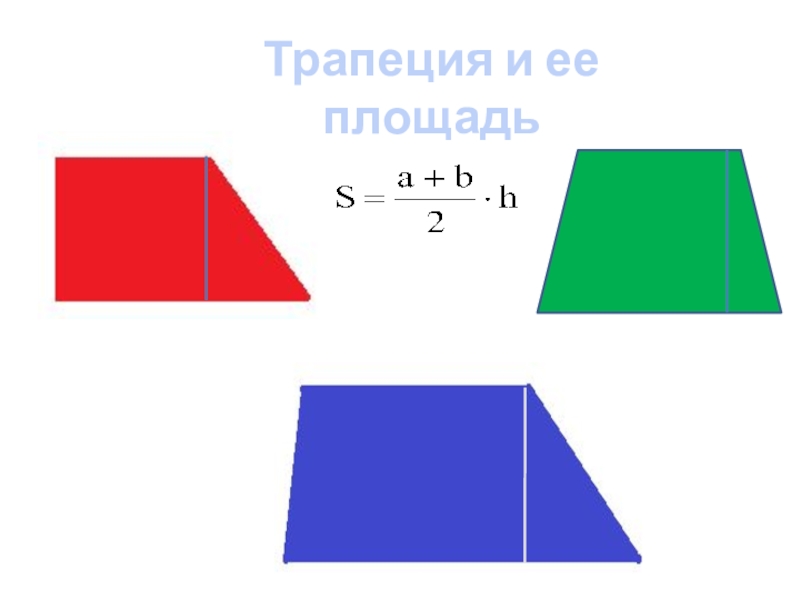
- 6. Трапеция и ее площадь
- 7. Криволинейной трапецией называется фигура, ограниченная
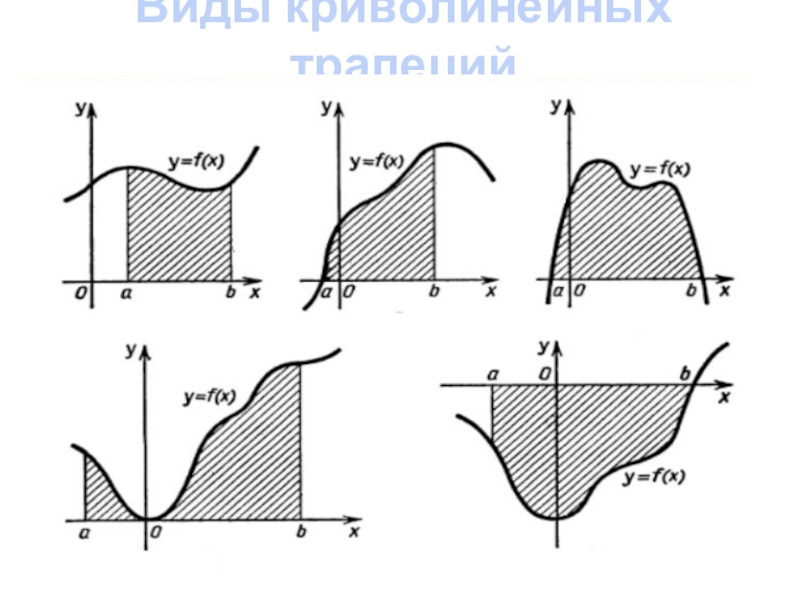
- 8. Виды криволинейных трапеций
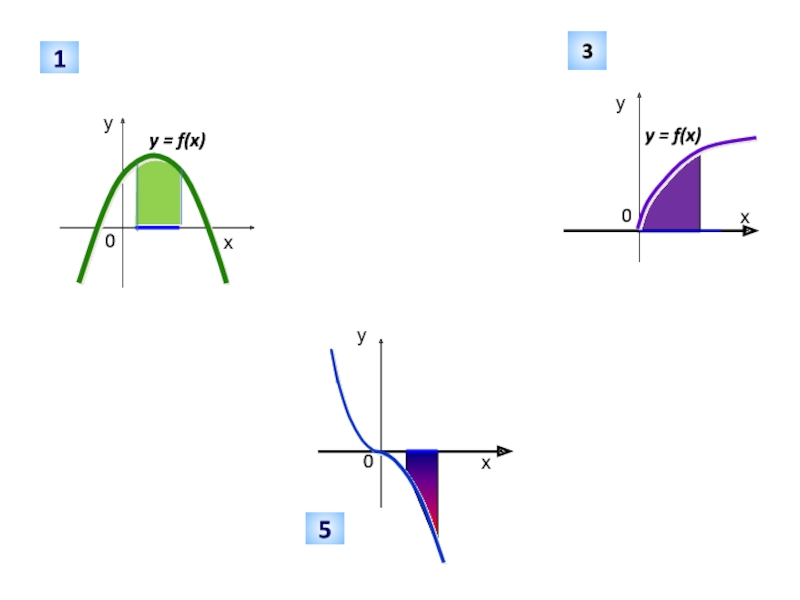
- 9. у1уууууУ=123y = f(x)y = f(x)y = f(x)y = f(x)y = f(x)У=3456Какие фигуры являются криволинейными трапециями
- 10. у1уу3y = f(x)y = f(x)5
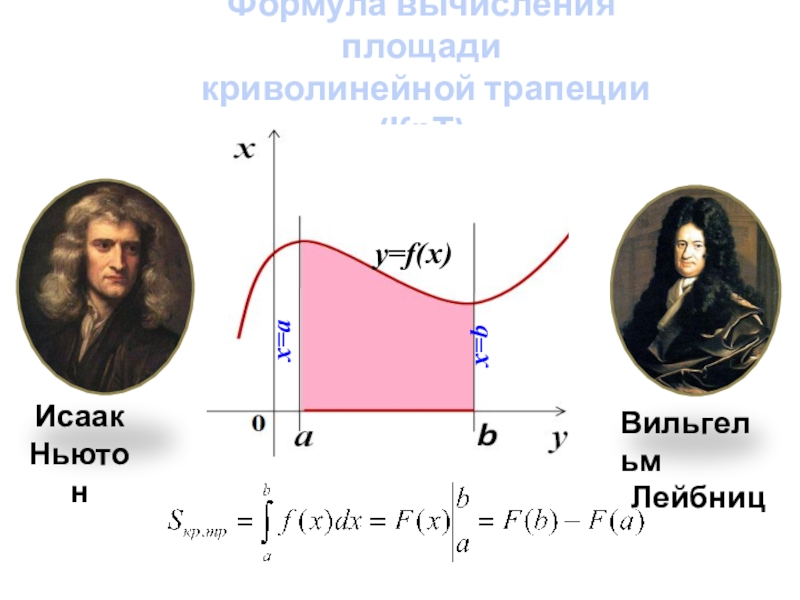
- 11. Формула вычисления площади криволинейной трапеции (КрТ)
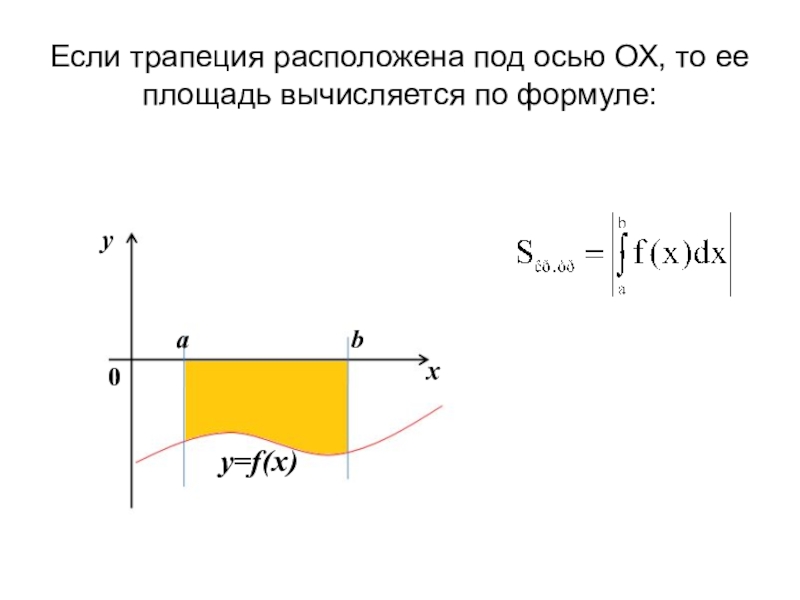
- 12. Если трапеция расположена под осью ОХ, то ее площадь вычисляется по формуле: х=a х=babxy0y=f(x)
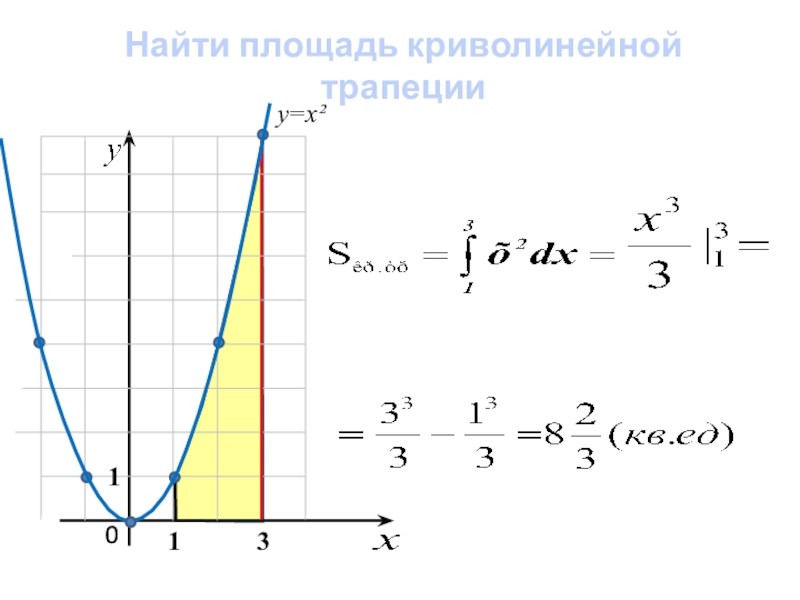
- 13. 013y=х²1Найти площадь криволинейной трапеции
- 14. Алгоритм нахождения SктПостроить график функции f(x). Провести
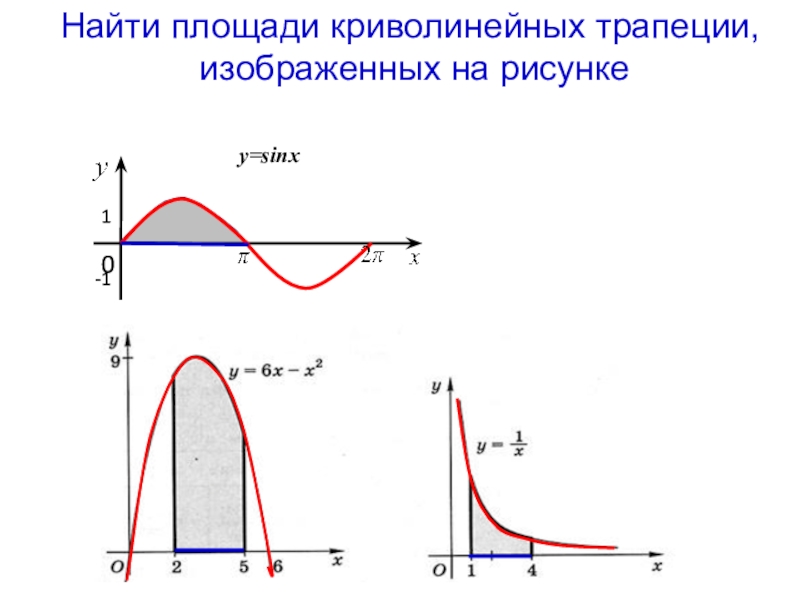
- 15. Найти площади криволинейных трапеции, изображенных на рисунке y=sinx1-1
Повторяем термины23167541.Зависимость переменной Y от переменной x, при которой каждому значению x ставится в соответствие единственное значение Y 2. Действие нахождения производной называется… 3. Символ, который обозначает производную 4. Если для всех x на некотором интервале
Слайд 2Повторяем термины
2
3
1
6
7
5
4
1.Зависимость переменной Y от переменной x, при которой каждому значению
x ставится в соответствие единственное значение Y
2. Действие нахождения производной называется…
3. Символ, который обозначает
производную
4. Если для всех x на
некотором интервале
выполняется равенство
F/(x)=f(x), то F(x) называется…
5. Действие,
обратное дифференцированию
6-7. Именами каких ученых названа формула вычисления определенного интеграла
Слайд 7 Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не
меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] -основание
криволинейной трапеции
Определение
![Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции](/img/thumbs/7886c4d3d66c03fced09dcec76f344ed-800x.jpg "Презентация к уроку по дисциплине Математика по теме Площадь криволинейной трапеции Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей")
Слайд 9у
1
у
у
у
у
у
У=1
2
3
y = f(x)
y = f(x)
y = f(x)
y = f(x)
y = f(x)
У=3
4
5
6
Какие
фигуры являются криволинейными трапециями
Слайд 12Если трапеция расположена под осью ОХ, то ее площадь вычисляется по
формуле:
х=a
х=b
a
b
x
y
0
y=f(x)
Слайд 14Алгоритм нахождения Sкт
Построить график функции f(x).
Провести прямые x=a, y=b
Убедиться, что
фигура является криволинейной
трапецией
4. Составить и вычислить определенный
интеграл, где f(x) –
подынтегральная функция,
a,b – пределы интегрирования
трапецией
4. Составить и вычислить определенный
интеграл, где f(x) –
подынтегральная функция,
a,b – пределы интегрирования
