- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Объём прямой призмы
Содержание
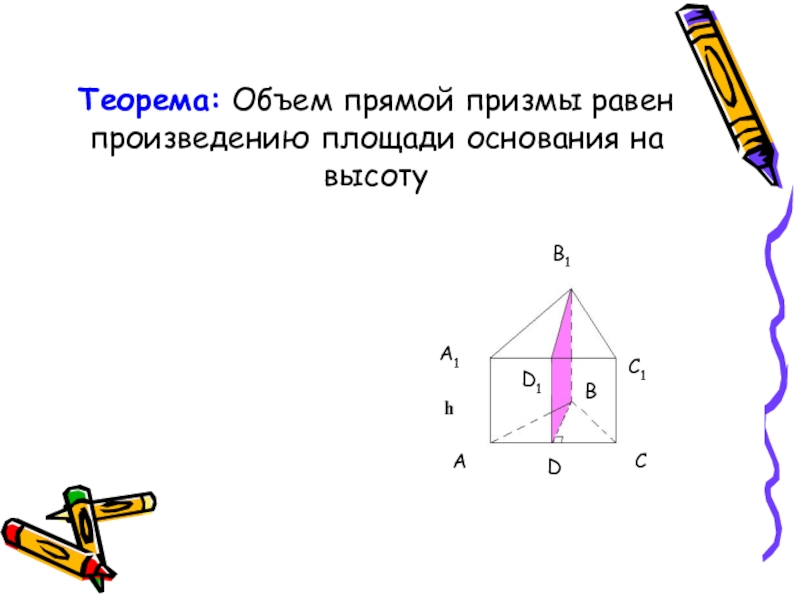
Теорема: Объем прямой призмы равен произведению площади основания на высотуВD1А1В1С1АCD
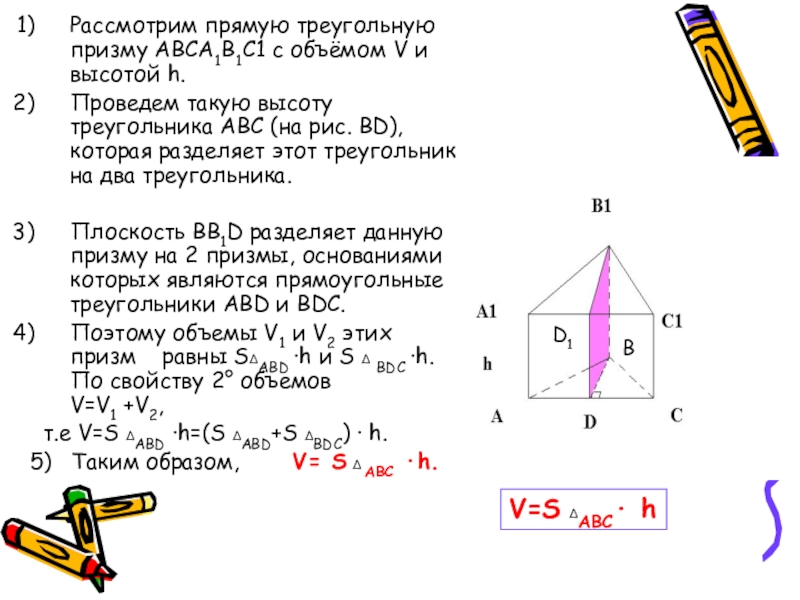
Слайд 3Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h.
Проведем
такую высоту треугольника ABC (на рис. BD),которая разделяет этот треугольник на два треугольника.
Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC.
Поэтому объемы V1 и V2 этих призм равны S∆ABD ·h и S ∆ BDC ·h. По свойству 2° объемов V=V1 +V2,
т.е V=S ∆ABD ·h=(S ∆ABD+S ∆BDC) · h.
5) Таким образом, V= S ∆ ABC ·h.
Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC.
Поэтому объемы V1 и V2 этих призм равны S∆ABD ·h и S ∆ BDC ·h. По свойству 2° объемов V=V1 +V2,
т.е V=S ∆ABD ·h=(S ∆ABD+S ∆BDC) · h.
5) Таким образом, V= S ∆ ABC ·h.
V=S ∆ABC∙ h
В
D1
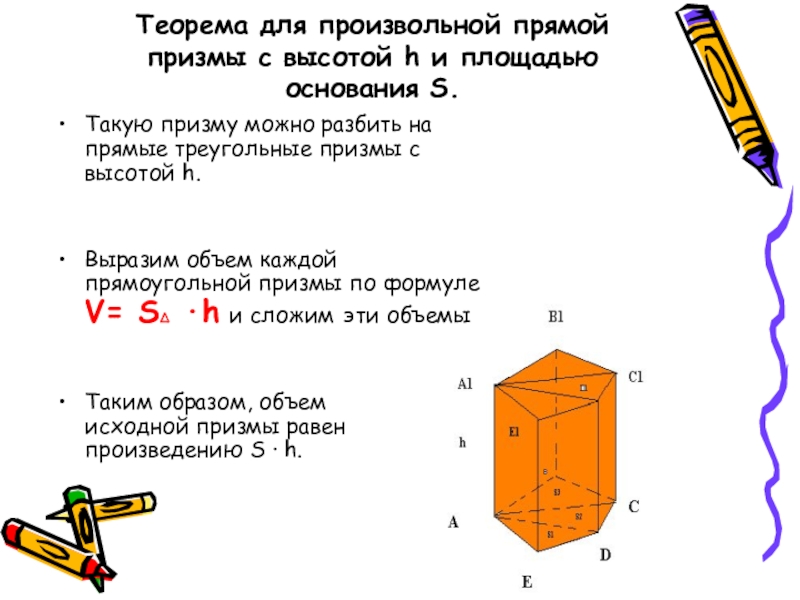
Слайд 4Теорема для произвольной прямой призмы с высотой h и площадью основания
S.
Такую призму можно разбить на прямые треугольные призмы с высотой h.
Выразим объем каждой прямоугольной призмы по формуле V= S∆ ·h и сложим эти объемы
Таким образом, объем исходной призмы равен произведению S · h.