планиметрические задачи. Подготовка к ЕГЭ. Задание №16.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку обобщающего повторения по геометрии в рамках подготовки к ЕГЭ по теме Многовариантные задачи
Содержание
- 1. Презентация к уроку обобщающего повторения по геометрии в рамках подготовки к ЕГЭ по теме Многовариантные задачи
- 2. Многовариантность задач возникает, в основном по нескольким
- 3. Причина: Неоднозначность в расположении точек на прямой.
- 4. Причина: Неоднозначность взаимного расположения окружностей. Где искать:
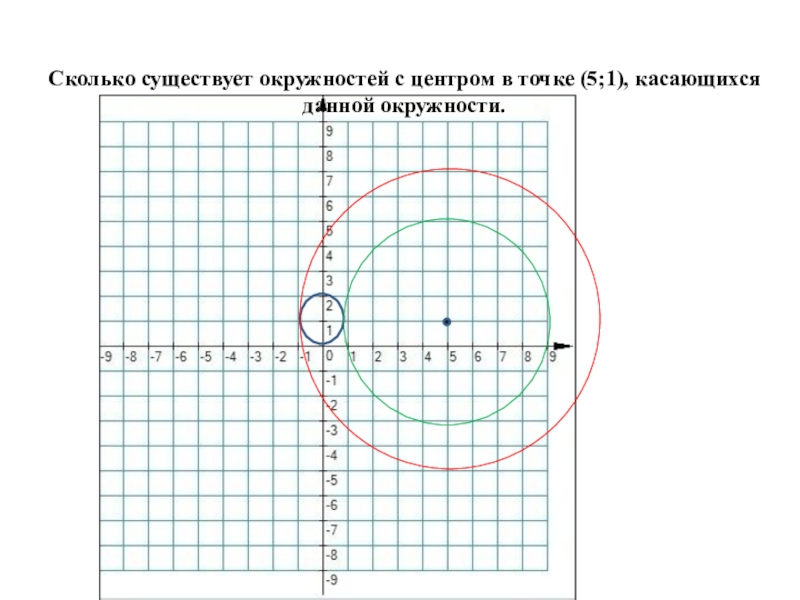
- 5. Сколько существует окружностей с центром в точке (5;1), касающихся данной окружности.
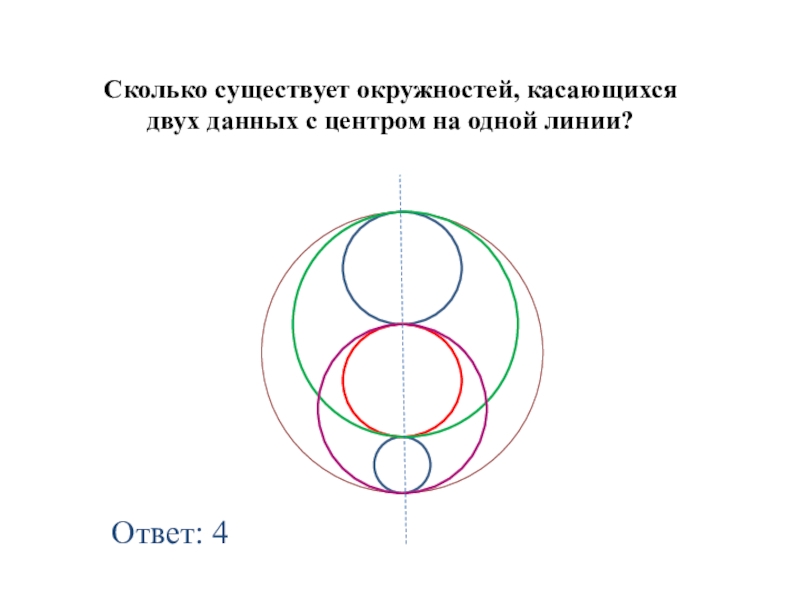
- 6. Ответ: 4Сколько существует окружностей, касающихся двух данных с центром на одной линии?
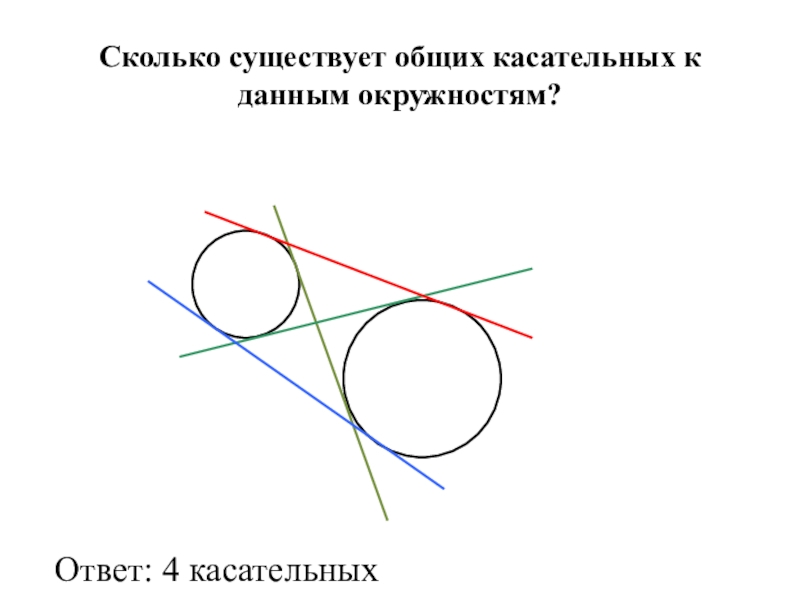
- 7. Сколько существует общих касательных к данным окружностям? Ответ: 4 касательных
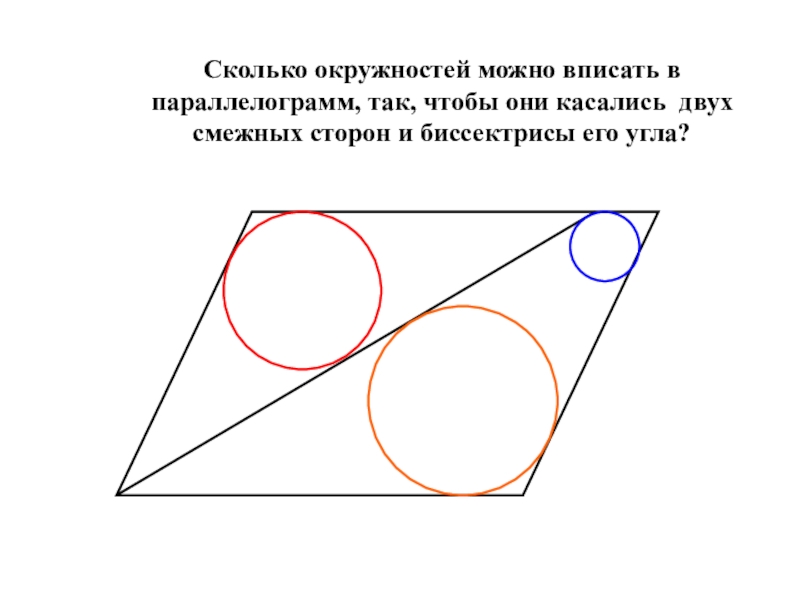
- 8. Сколько окружностей можно вписать в параллелограмм, так,
- 9. ABCLKЗадача №1В треугольнике ABC известны стороны AB
- 10. 2случай.BACLK∆ KBL~∆ CBA∠B – общий, ∠AKL =
- 11. Задача №2В треугольнике угол C равен 600.
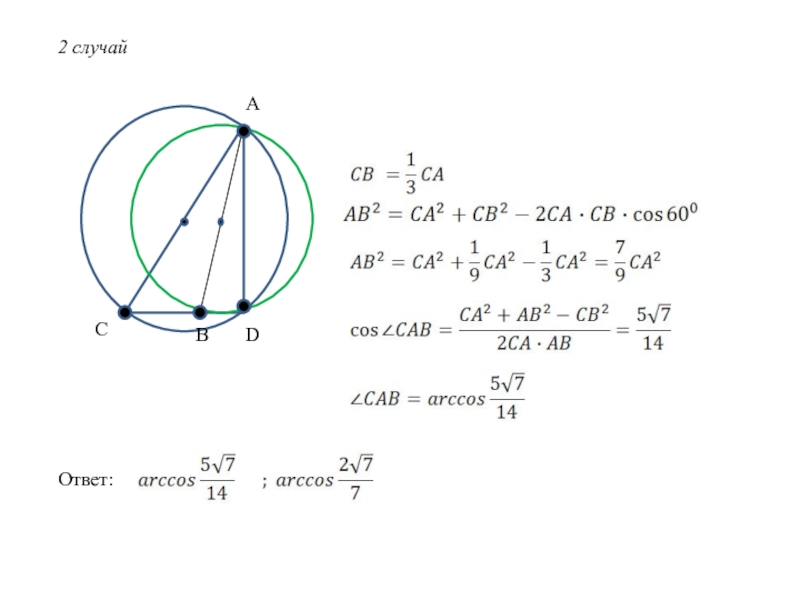
- 12. ADCB2 случайОтвет:
- 13. Задача №3.В окружность радиуса
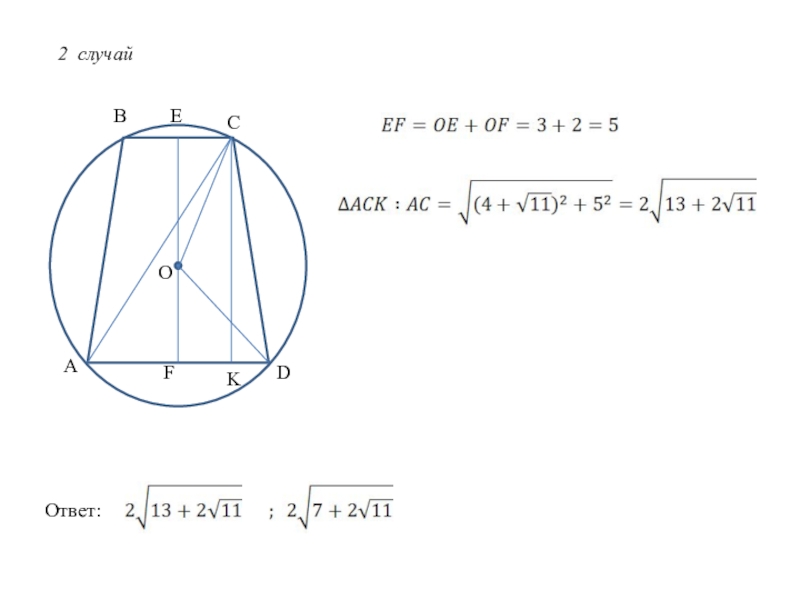
- 14. 2 случайABCDFKOEОтвет:
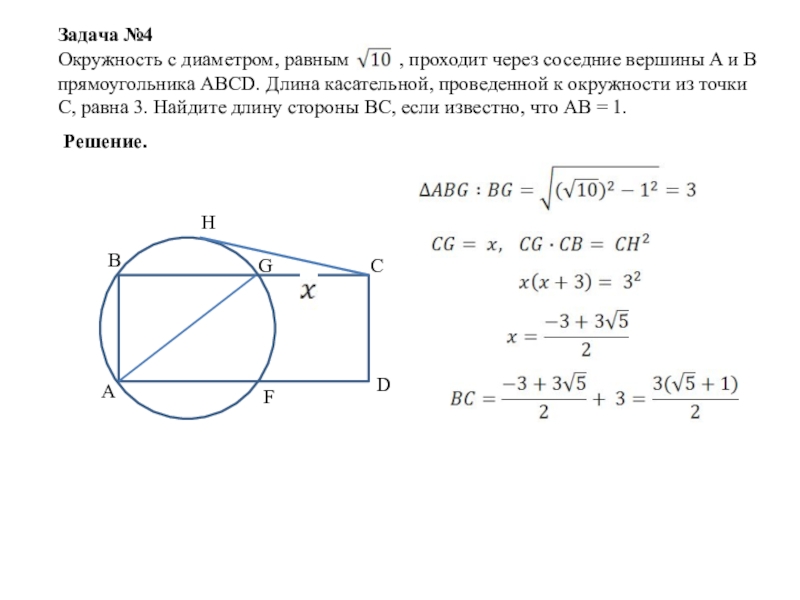
- 15. Задача №4Oкружность с диаметром, равным
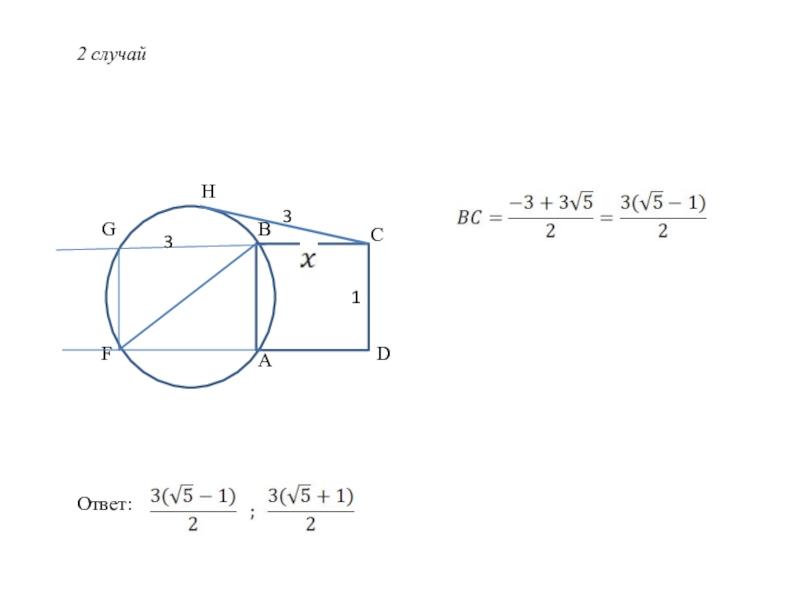
- 16. 2 случайABCDGFH331Ответ:
- 17. Задача №5В равнобедренный треугольник с основанием 12
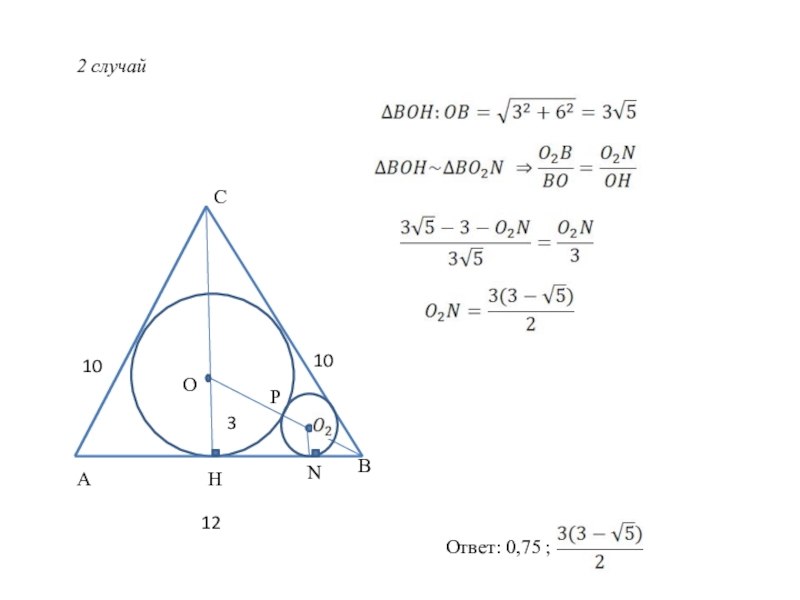
- 18. СHABO10102 случайNP312Ответ: 0,75 ;
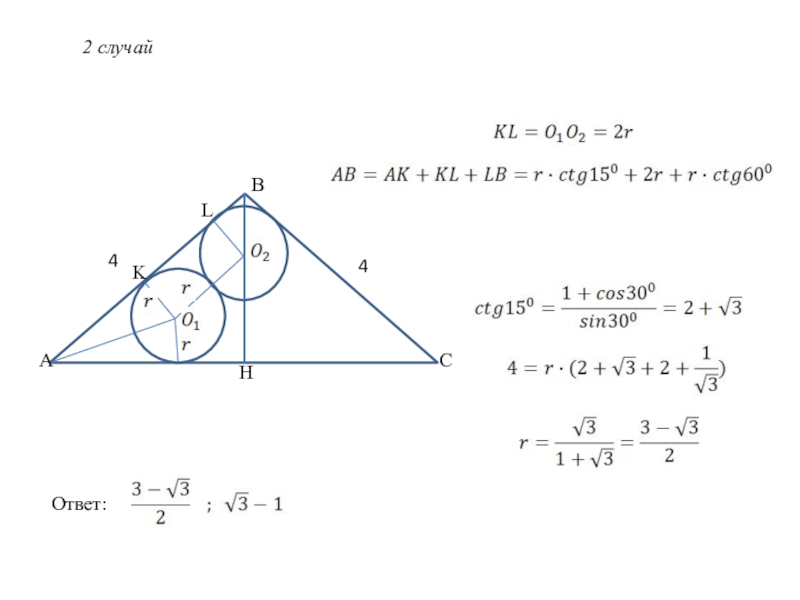
- 19. Задача №6Дан равнобедренный треугольник с боковой стороной
- 20. BC44HLKA2 случайОтвет:
- 21. Задача №7Найдите радиус окружности, вписанной в угол
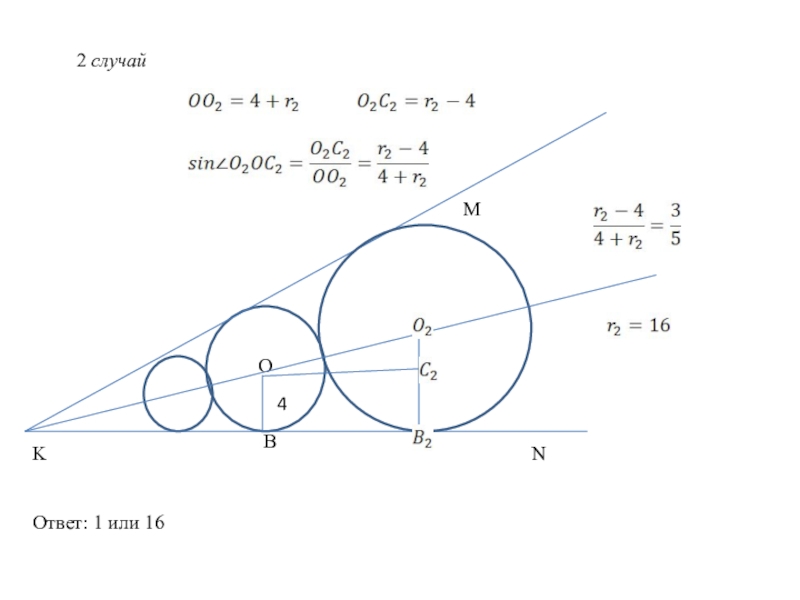
- 22. 2 случайMKNOB4Ответ: 1 или 16
- 23. Задача №8Вершина равнобедренного треугольника с боковой стороной
- 24. Если вы хотите научиться плавать, то смело
Многовариантность задач возникает, в основном по нескольким причинам: неоднозначность при задании взаимного расположения элементов в фигуре; - неоднозначность при задании взаимного расположения нескольких фигур в комбинационных задачах.
Слайд 1Многовариантные задачи.
Окружность.
Учитель: Шарова Светлана Геннадьевна,
МБОУ «Гимназия», г. Урюпинск, Волгоградская область
Учимся решать
Слайд 2Многовариантность задач возникает, в основном по нескольким причинам:
неоднозначность при
задании взаимного расположения элементов в фигуре;
- неоднозначность при задании взаимного расположения нескольких фигур в комбинационных задачах.
- неоднозначность при задании взаимного расположения нескольких фигур в комбинационных задачах.
Слайд 3Причина: Неоднозначность в расположении точек на прямой.
Где искать: в условиях
задачи нет точного указания, в каком порядке располагаются точки на прямой.
Причина: Неоднозначность в расположении точек относительно прямой.
Где искать: в условиях задачи нет точного указания, где именно (в какой полуплоскости) располагается точка относительно прямой или кривой.
Причина: Неоднозначность в выборе обозначений вершин многоугольника.
Где искать: в условиях задачи либо нет описания обозначения вершин, либо нет указания, в каком порядке они перечисляются.
Причина: Неоднозначность в выборе заданного элемента фигуры.
Где искать: в условиях задачи заданы величины (сторон и углов), но не указана их точная принадлежность какому-либо обозначенному элементу фигуры.
Причина: Неоднозначность взаимного расположения многоугольников.
Где искать: в условиях задачи нет точного указания, где именно располагается одна фигура относительно другой.
Слайд 4Причина: Неоднозначность взаимного расположения окружностей.
Где искать:
- случаи касания окружностей
(внешнее и внутреннее);
- случаи пересечения окружностей (положение центров относительно общей хорды);
- расположение точек касания нескольких окружностей с прямой.
- случаи пересечения окружностей (положение центров относительно общей хорды);
- расположение точек касания нескольких окружностей с прямой.
Слайд 8Сколько окружностей можно вписать в параллелограмм, так, чтобы они касались двух
смежных сторон и биссектрисы его угла?
Слайд 9A
B
C
L
K
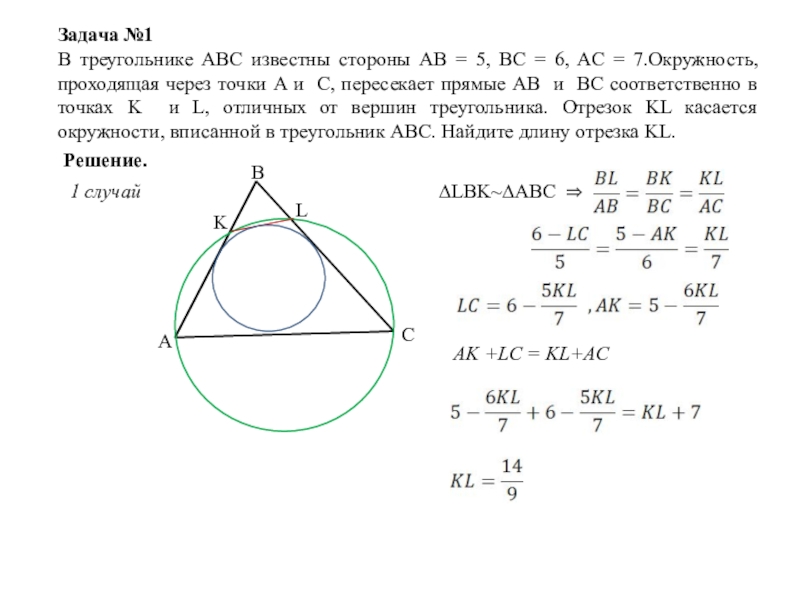
Задача №1
В треугольнике ABC известны стороны AB = 5, BC =
6, AC = 7.Окружность, проходящая через точки A и C, пересекает прямые AB и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.
Решение.
1 случай
∆LBK~∆ABC ⇒
AK +LC = KL+AC
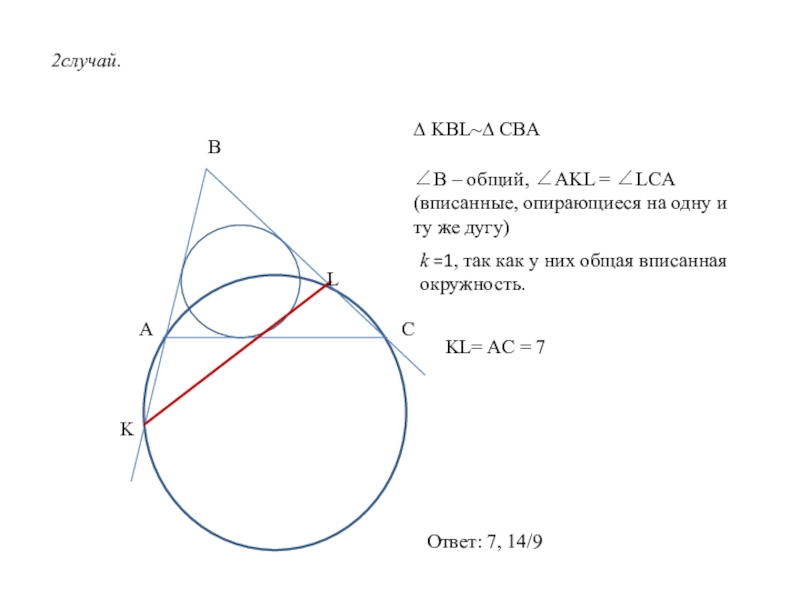
Слайд 102случай.
B
A
C
L
K
∆ KBL~∆ CBA
∠B – общий, ∠AKL = ∠LCA (вписанные, опирающиеся на
одну и ту же дугу)
k =1, так как у них общая вписанная окружность.
KL= AC = 7
Ответ: 7, 14/9
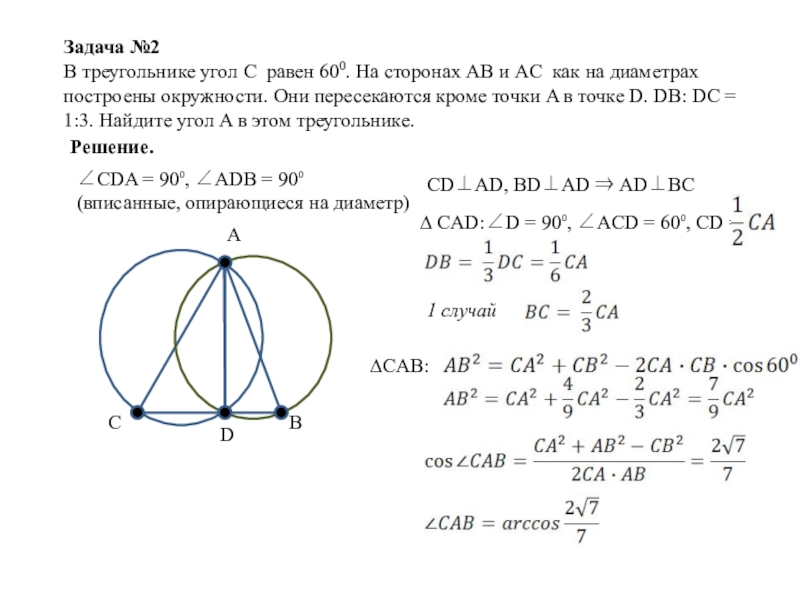
Слайд 11Задача №2
В треугольнике угол C равен 600. На сторонах AB и
AC как на диаметрах построены окружности. Они пересекаются кроме точки A в точке D. DB: DC = 1:3. Найдите угол A в этом треугольнике.
Решение.
A
B
C
D
1 случай
∠CDA = 90⁰, ∠ADB = 90⁰ (вписанные, опирающиеся на диаметр)
CD⊥AD, BD⊥AD ⇒ AD⊥BC
∆ CAD:∠D = 90⁰, ∠ACD = 60⁰, CD =
∆CAB:
Слайд 13Задача №3.
В окружность радиуса вписана трапеция
с основаниями 8 и . Найдите длину диагонали трапеции.
Решение.
1 случай
A
B
C
D
E
O
F
K
Слайд 15Задача №4
Oкружность с диаметром, равным , проходит
через соседние вершины A и B прямоугольника ABCD. Длина касательной, проведенной к окружности из точки C, равна 3. Найдите длину стороны BC, если известно, что AB = 1.
Решение.
A
B
C
D
G
F
H
Слайд 17Задача №5
В равнобедренный треугольник с основанием 12 и боковой стороной 10
вписана окружность. Вторая окружность касается двух сторон треугольника и первой окружности. Найдите радиус второй окружности.
Решение.
1 случай
С
H
A
B
O
F
S
D
E
12
10
10
M
DE║AB
∆ DEC: CM=CH – 2r = 8-6 = 2
∆ ABC ~∆DEC⇒
Слайд 19Задача №6
Дан равнобедренный треугольник с боковой стороной равной 4 и углом
1200. Внутрь треугольника вписаны две равные окружности таким образом, что окружности касаются друг друга и каждая окружность касается двух сторон треугольника. Найдите радиус окружности.
Решение.
A
B
C
H
4
4
120⁰
∠ A = ∠ C = 30⁰,
1 случай
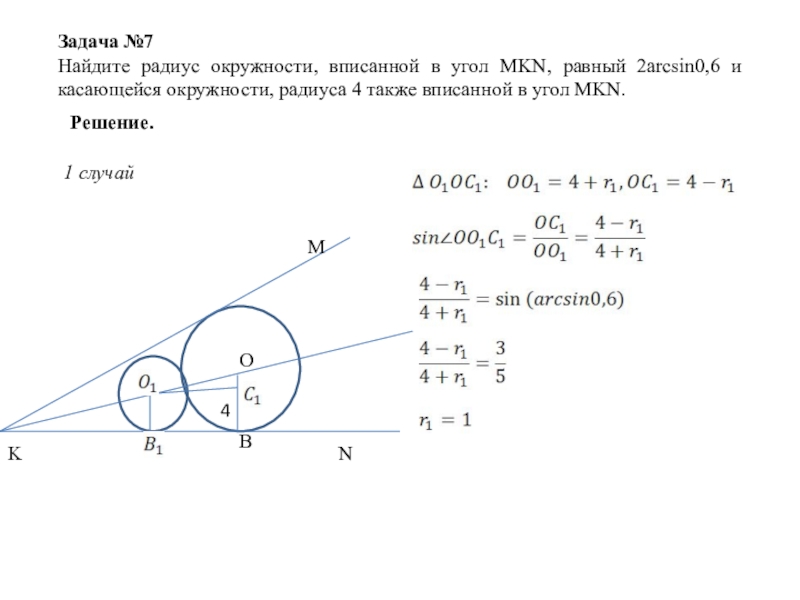
Слайд 21Задача №7
Найдите радиус окружности, вписанной в угол MKN, равный 2arcsin0,6 и
касающейся окружности, радиуса 4 также вписанной в угол MKN.
Решение.
M
K
N
O
B
1 случай
4
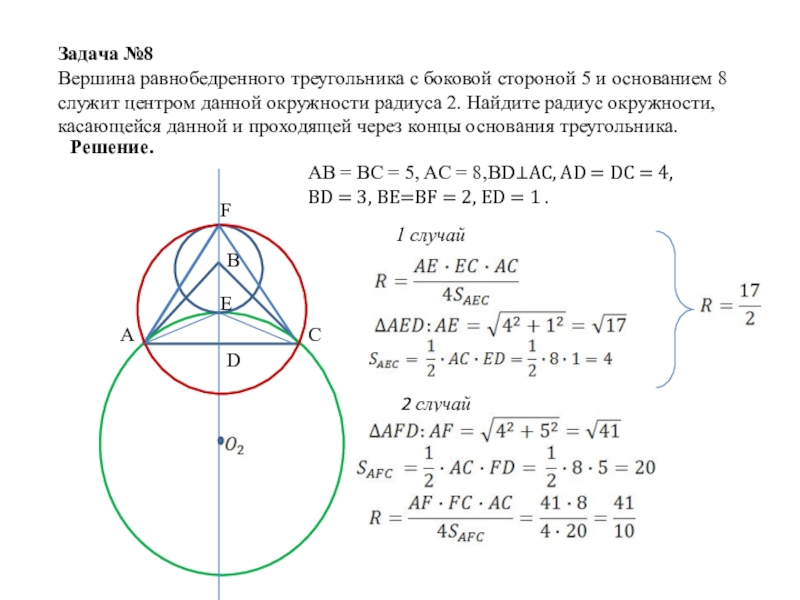
Слайд 23Задача №8
Вершина равнобедренного треугольника с боковой стороной 5 и основанием 8
служит центром данной окружности радиуса 2. Найдите радиус окружности, касающейся данной и проходящей через концы основания треугольника.
Решение.
A
F
B
C
E
D
AB = BC = 5, AC = 8,BD⊥AC, AD = DC = 4, BD = 3, BE=BF = 2, ED = 1 .
1 случай
2 случай
Слайд 24Если вы хотите научиться плавать, то смело входите в воду, а
если хотите научиться решать задачи, то решайте их!
Д. Пойа.
