- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку на тему Тетраэдр
Содержание
- 1. Презентация к уроку на тему Тетраэдр
- 2. Цели урока:Формирование у учащихся навыков решения задач
- 3. Что такое «сечение»? Сечение – это изображение фигуры,
- 4. А1Через любые три точки, не лежащие на
- 5. Тетраэдр – поверхность, составленная из четырех треугольников.Плоскость
- 6. NPBAMПостроить сечения тетраэдра NABP плоскостью, проходящей через данные точки: N, P, M.№1
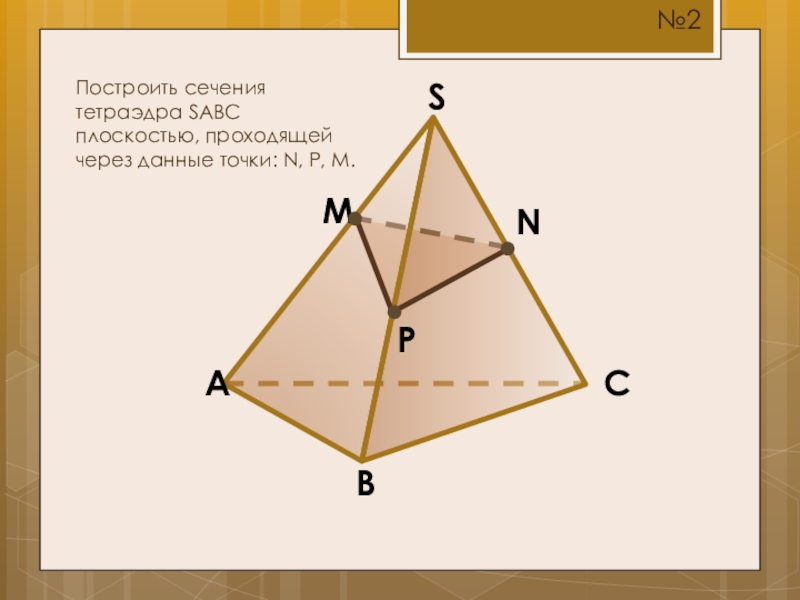
- 7. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№2
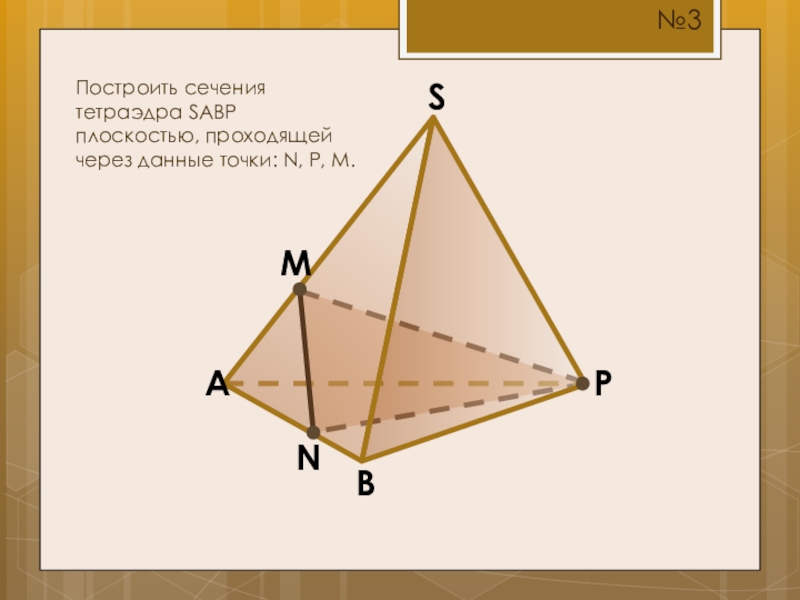
- 8. SBAMПостроить сечения тетраэдра SABP плоскостью, проходящей через данные точки: N, P, M.NP№3
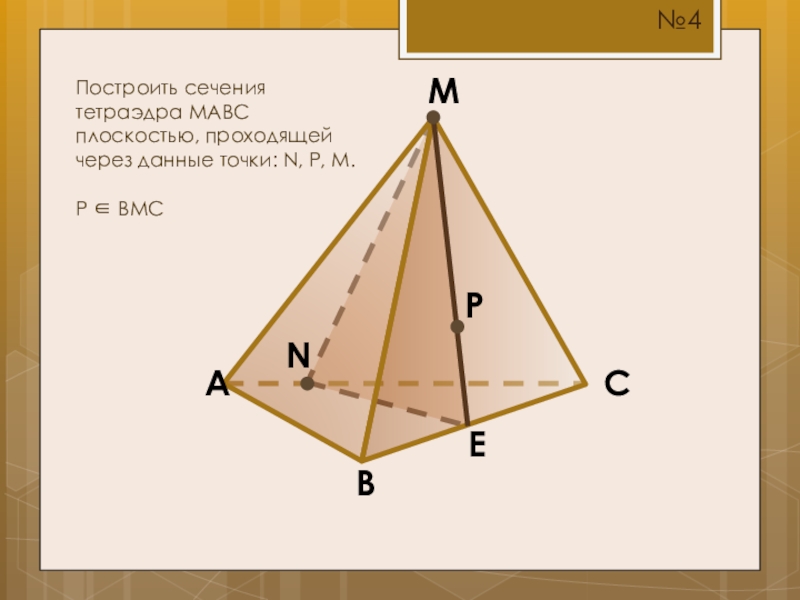
- 9. MCBAПостроить сечения тетраэдра MABC плоскостью, проходящей через данные точки: N, P, M.P BMCNPE№4
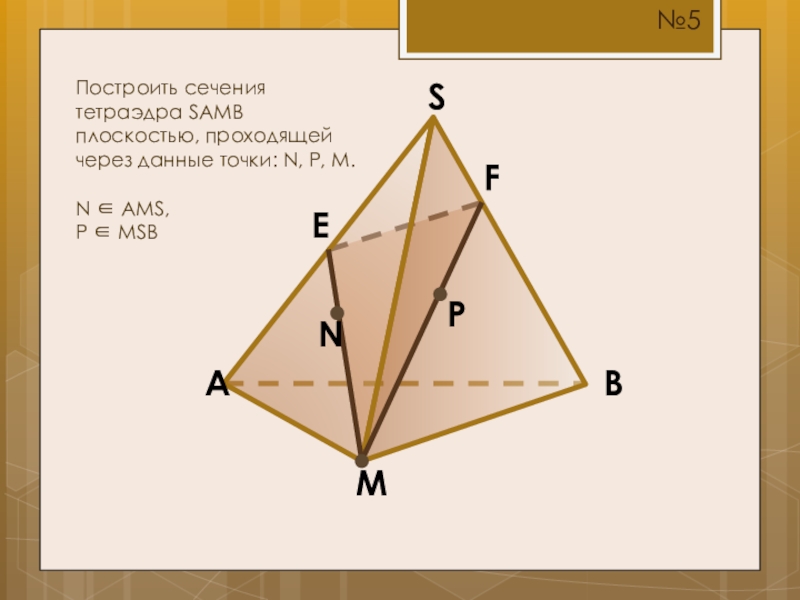
- 10. SBMAПостроить сечения тетраэдра SAMB плоскостью, проходящей через данные точки: N, P, M.N AMS,P MSBNPEF№5
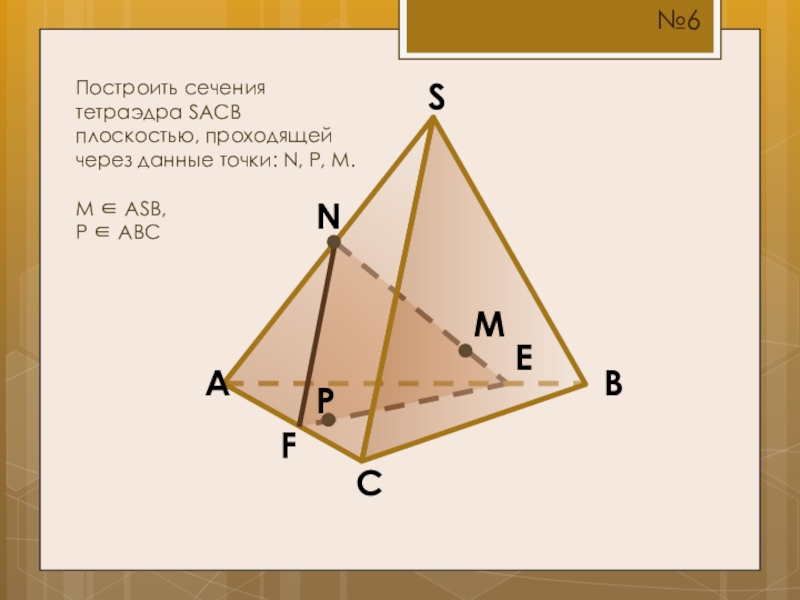
- 11. SBCAMПостроить сечения тетраэдра SACB плоскостью, проходящей через данные точки: N, P, M.M ASB,P ABCNPEF№6
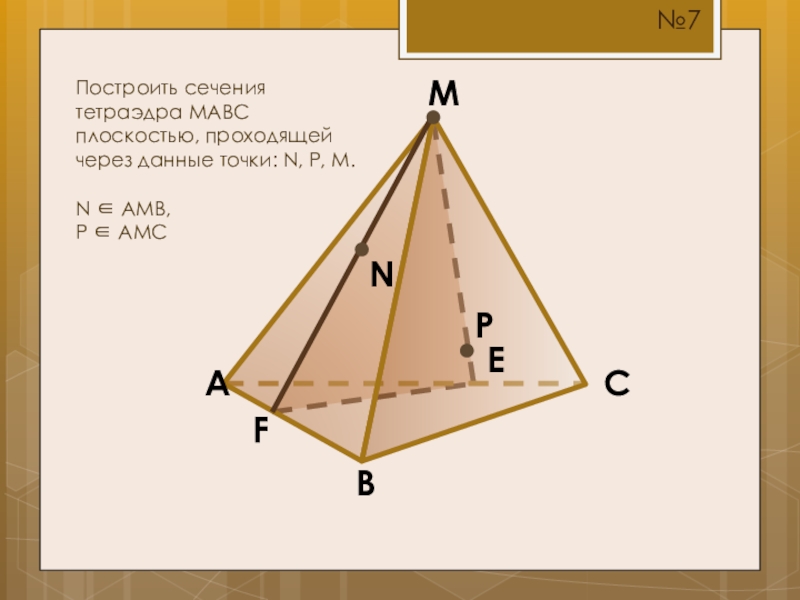
- 12. MCBAПостроить сечения тетраэдра MABC плоскостью, проходящей через данные точки: N, P, M.N AMB,P AMCNP№7EF
- 13. PSCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.N№8OE
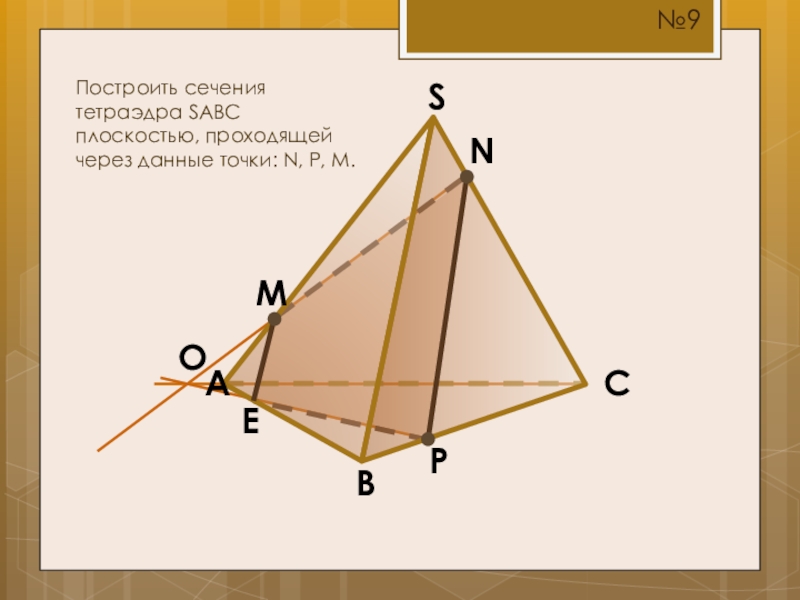
- 14. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№9OE
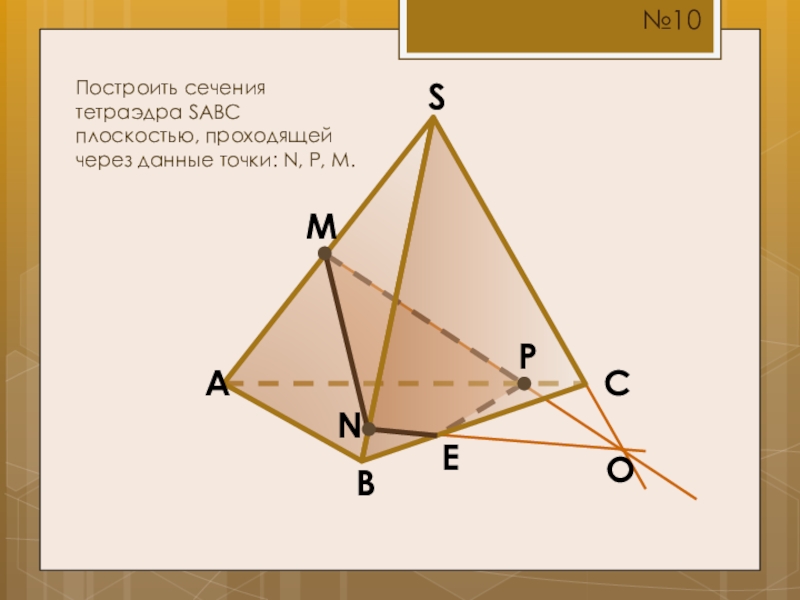
- 15. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№10OE
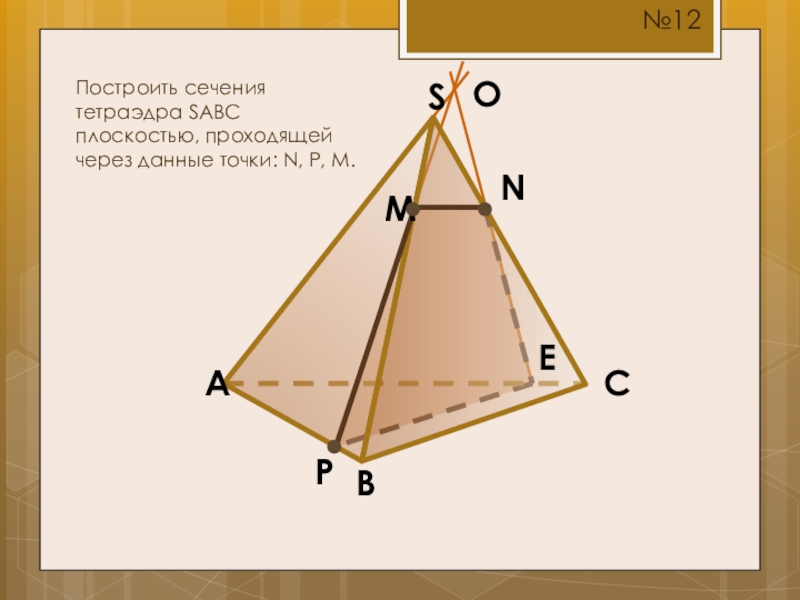
- 16. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№12OE
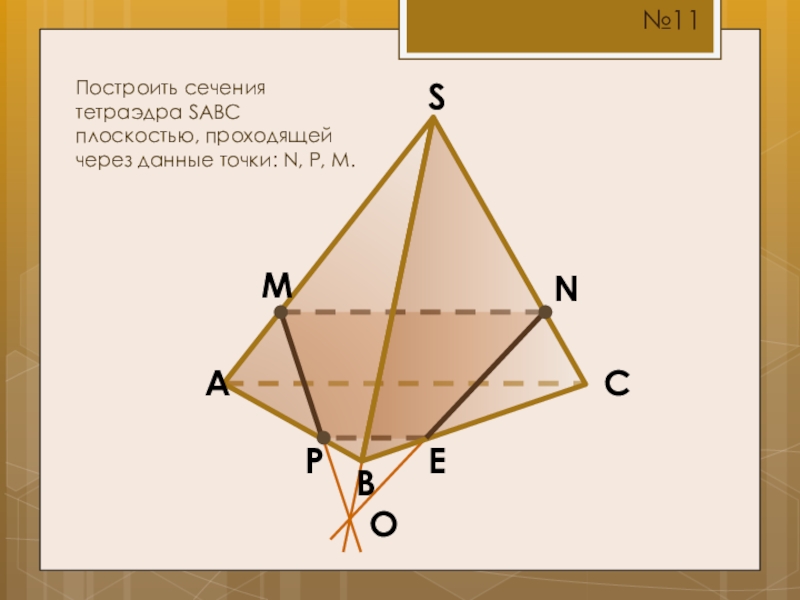
- 17. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№11OE
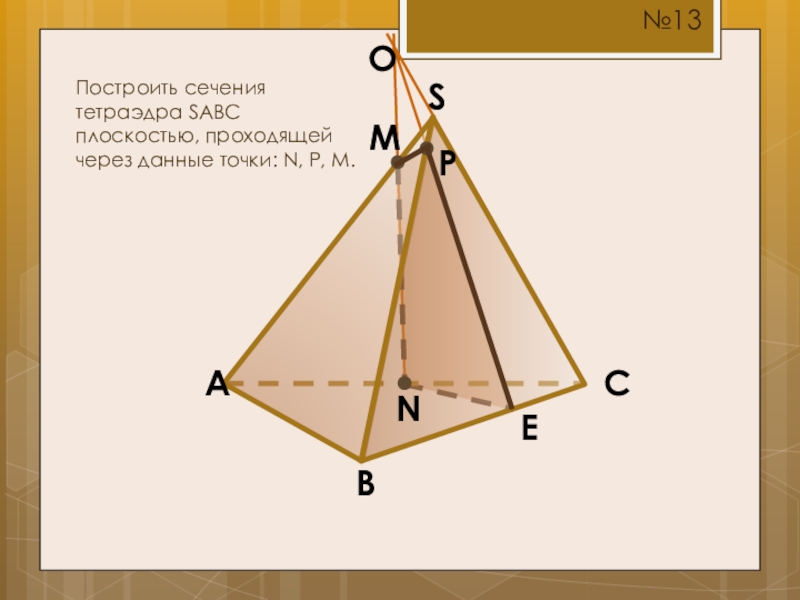
- 18. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№13OE
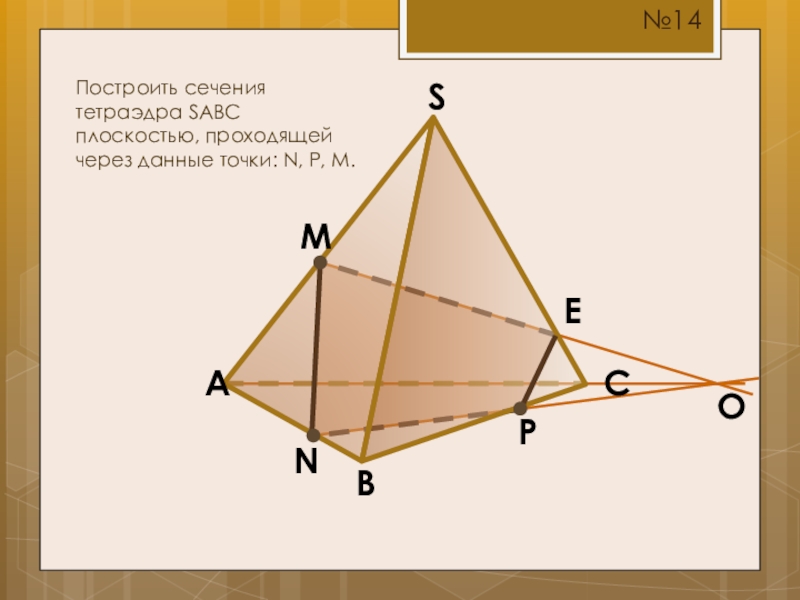
- 19. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№14OE
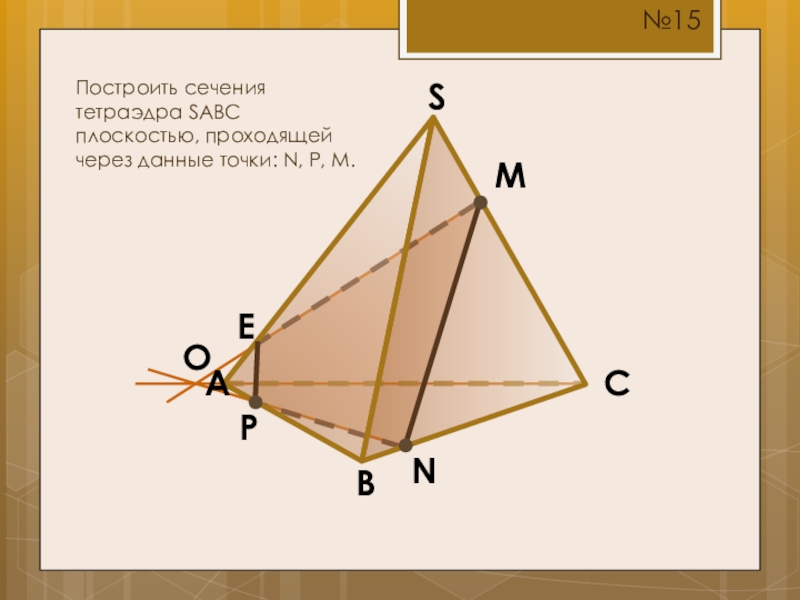
- 20. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№15OE
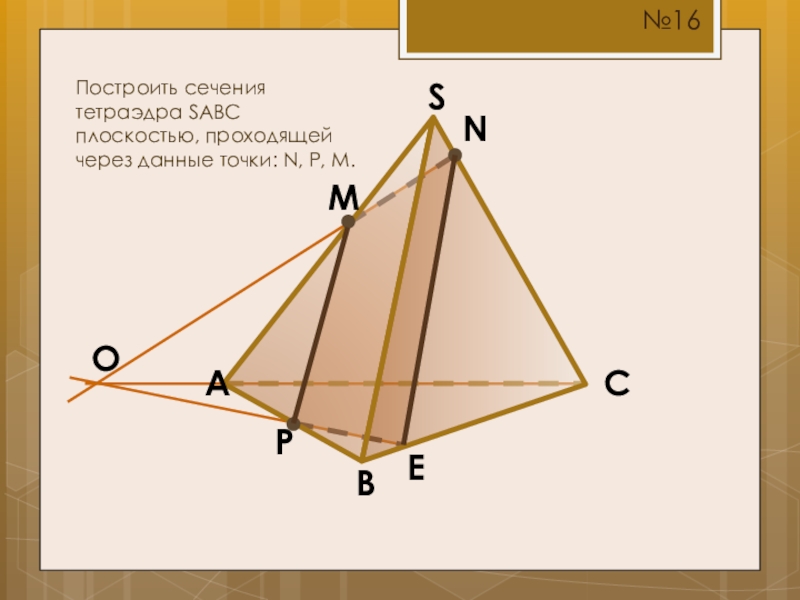
- 21. SCBAMПостроить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P, M.NP№16OE
- 22. Итоги урока:Научились применять аксиомы стереометрии при решении
- 23. Домашнее заданиеСоставить 4 задачи на построение сечений многогранников.
Слайд 2Цели урока:
Формирование у учащихся навыков решения задач на построение сечений методом
Формирование и развитие у учащихся пространственного воображения.
Развитие графической культуры и математической речи.
Слайд 3Что такое «сечение»?
Сечение – это изображение фигуры, которая получается при мысленном
Какие виды сечений могут быть в тетраэдре и параллелепипеде?
В тетраэдре сечениями могут быть только треугольники или четырехугольники, а в параллелепипеде – треугольники, четырехугольники, пятиугольники или шестиугольники.
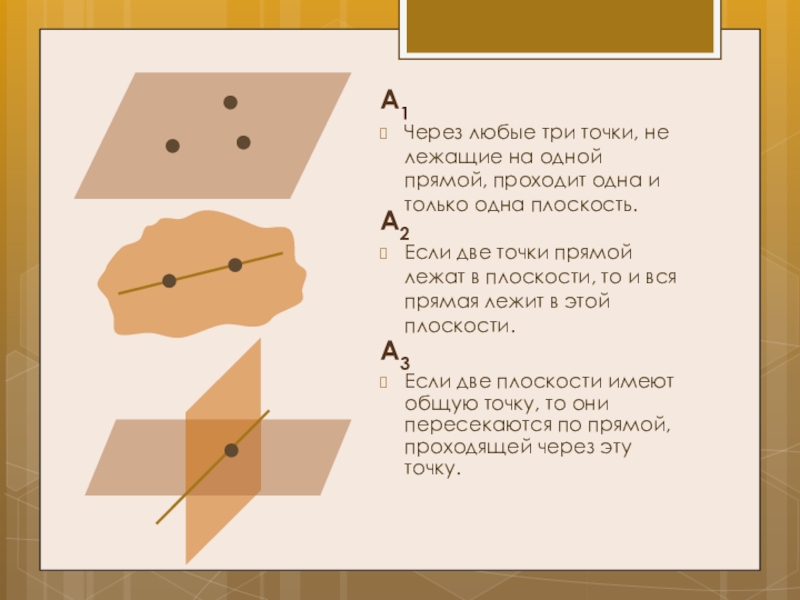
Слайд 4А1
Через любые три точки, не лежащие на одной прямой, проходит одна
А2
Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.
А3
Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
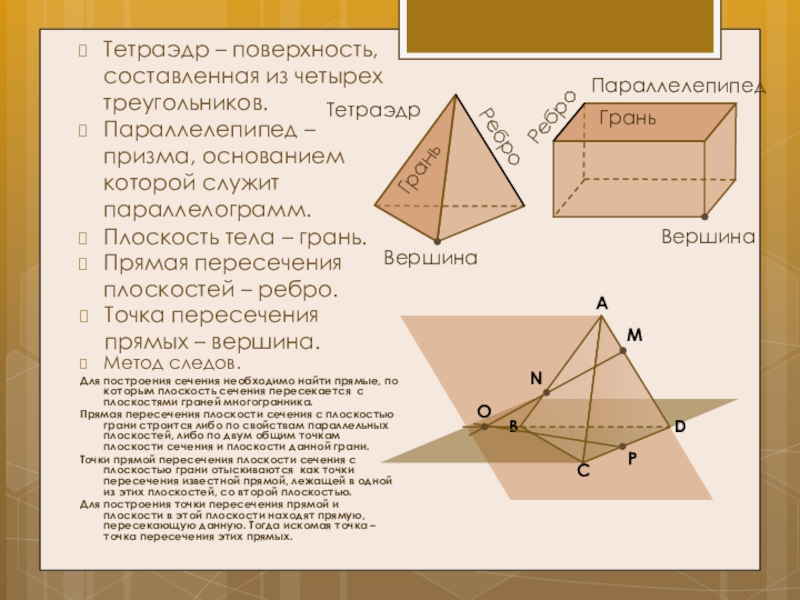
Слайд 5Тетраэдр – поверхность, составленная из четырех треугольников.
Плоскость тела – грань.
Прямая пересечения
Точка пересечения прямых – вершина.
Вершина
Параллелепипед – призма, основанием которой служит параллелограмм.
Вершина
B
A
C
D
N
M
P
O
Метод следов.
Для построения сечения необходимо найти прямые, по которым плоскость сечения пересекается с плоскостями граней многогранника.
Прямая пересечения плоскости сечения с плоскостью грани строится либо по свойствам параллельных плоскостей, либо по двум общим точкам плоскости сечения и плоскости данной грани.
Точки прямой пересечения плоскости сечения с плоскостью грани отыскиваются как точки пересечения известной прямой, лежащей в одной из этих плоскостей, со второй плоскостью.
Для построения точки пересечения прямой и плоскости в этой плоскости находят прямую, пересекающую данную. Тогда искомая точка – точка пересечения этих прямых.
Тетраэдр
Грань
Ребро
Параллелепипед
Грань
Ребро
Слайд 7S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№2
Слайд 9M
C
B
A
Построить сечения тетраэдра MABC плоскостью, проходящей через данные точки: N, P,
P BMC
N
P
E
№4
Слайд 10S
B
M
A
Построить сечения тетраэдра SAMB плоскостью, проходящей через данные точки: N, P,
N AMS,
P MSB
N
P
E
F
№5
Слайд 11S
B
C
A
M
Построить сечения тетраэдра SACB плоскостью, проходящей через данные точки: N, P,
M ASB,
P ABC
N
P
E
F
№6
Слайд 12M
C
B
A
Построить сечения тетраэдра MABC плоскостью, проходящей через данные точки: N, P,
N AMB,
P AMC
N
P
№7
E
F
Слайд 13P
S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
№8
O
E
Слайд 14S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№9
O
E
Слайд 15S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№10
O
E
Слайд 16S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№12
O
E
Слайд 17S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№11
O
E
Слайд 18S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№13
O
E
Слайд 19S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№14
O
E
Слайд 20S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№15
O
E
Слайд 21S
C
B
A
M
Построить сечения тетраэдра SABC плоскостью, проходящей через данные точки: N, P,
N
P
№16
O
E
Слайд 22Итоги урока:
Научились применять аксиомы стереометрии при решении задач;
Научились находить положение
Освоили методы построения этих сечений.