классе
Автор: Кудышева Ольга Георгиевна,
учитель математики МАОУ Ивановская СОШ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики в 10 классе Симметрия в пространстве.Понятие правильного многоугольника
Содержание
- 1. Презентация к уроку математики в 10 классе Симметрия в пространстве.Понятие правильного многоугольника
- 2. Симметрия … есть идея,с помощью которой человек
- 3. Что такое симметрия?Симметрия в переводе с греческого
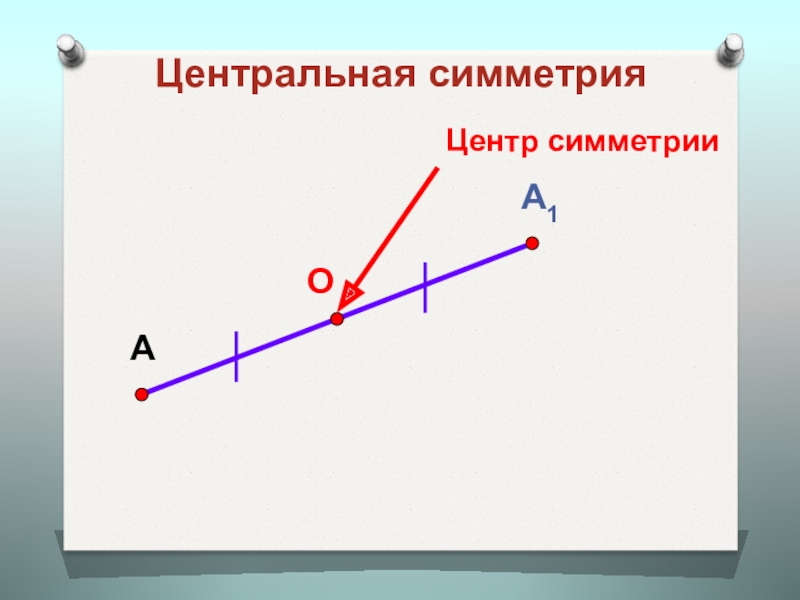
- 4. Центральная симметрияАА1ОЦентр симметрии
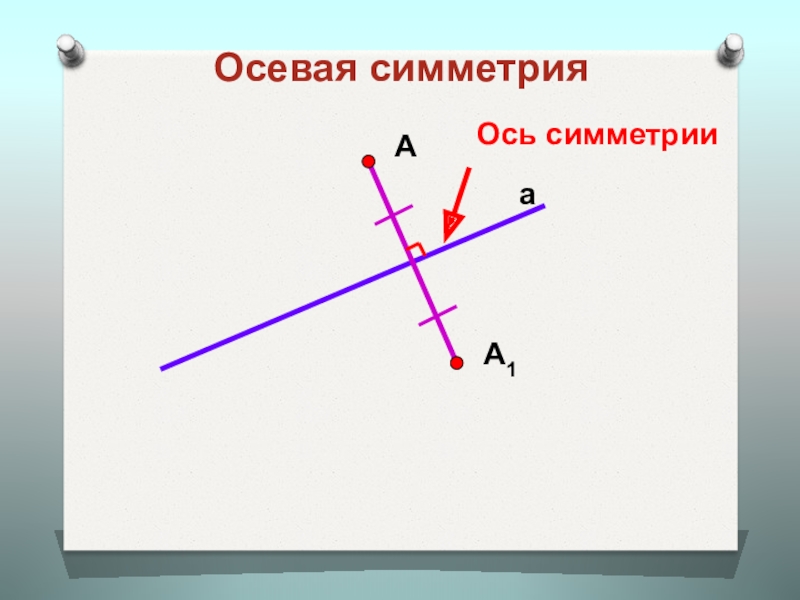
- 5. Осевая симметрияaАА1Ось симметрии
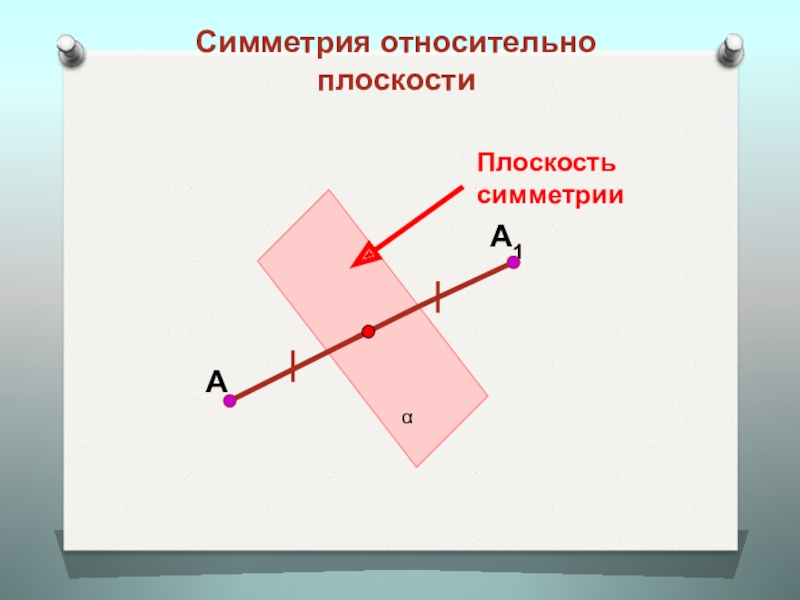
- 6. Симметрия относительно плоскостиАА1αПлоскость симметрии
- 7. СИММЕТРИЯ В ПРОСТРАНСТВЕ «Что может быть более
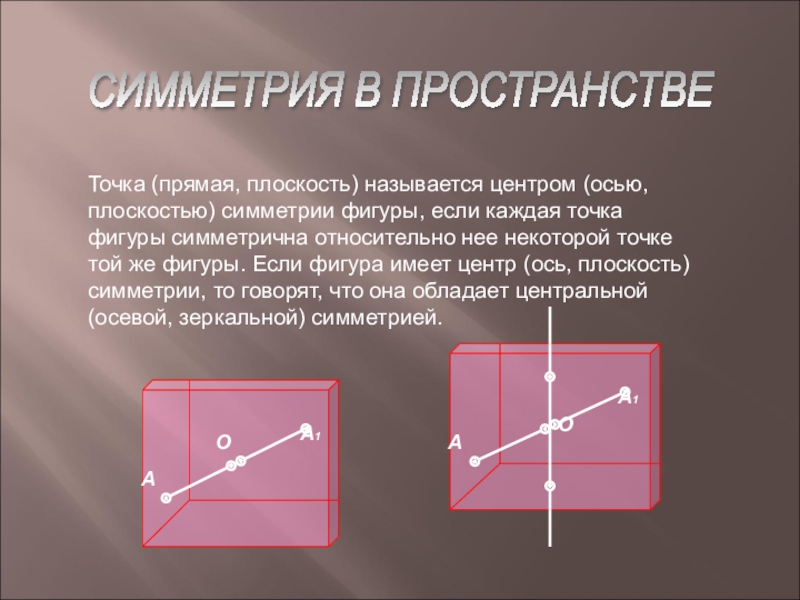
- 8. СИММЕТРИЯ В ПРОСТРАНСТВЕ Точка (прямая, плоскость) называется
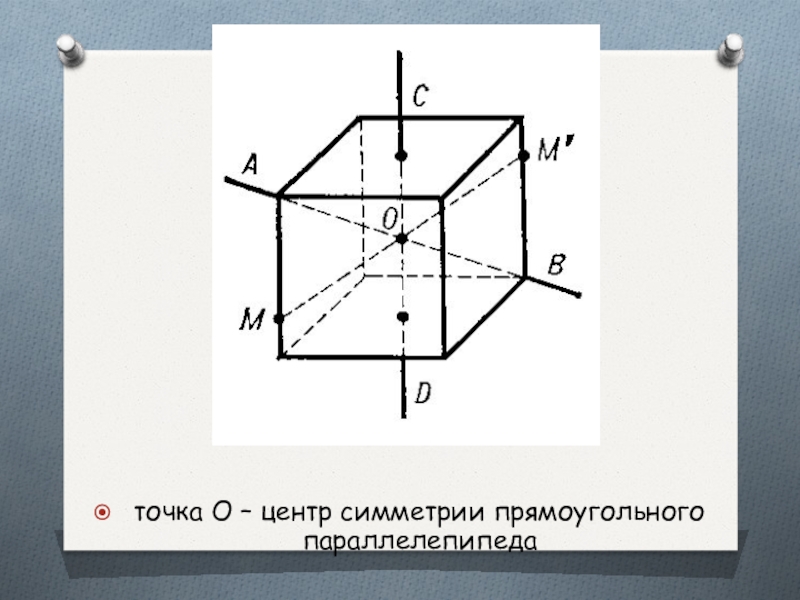
- 9. точка О – центр симметрии прямоугольного параллелепипеда
- 10. Симметрия в природе
- 11. Симметрия в природе
- 12. Многие атомы в пространстве располагаются по принципу
- 13. Симметрия в архитектуре
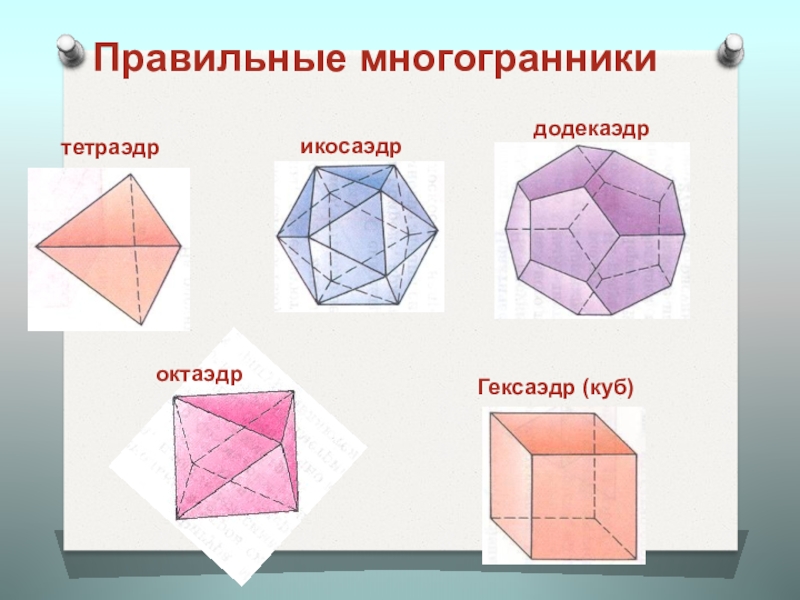
- 14. Правильные многогранникитетраэдрГексаэдр (куб)октаэдрикосаэдрдодекаэдр
- 15. Правильный тетраэдрсоставлен из четырех равносторонних треугольников. Каждая
- 16. Элементы симметрии: Тетраэдр не имеет центра симметрии,
- 17. Куб (гексаэдр)составлен из шести квадратов. Каждая вершина
- 18. Элементы симметрии: Куб имеет центр симметрии -
- 19. Правильный октаэдрсоставлен из восьми равносторонних треугольников. Каждая
- 20. Элементы симметрии: Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.
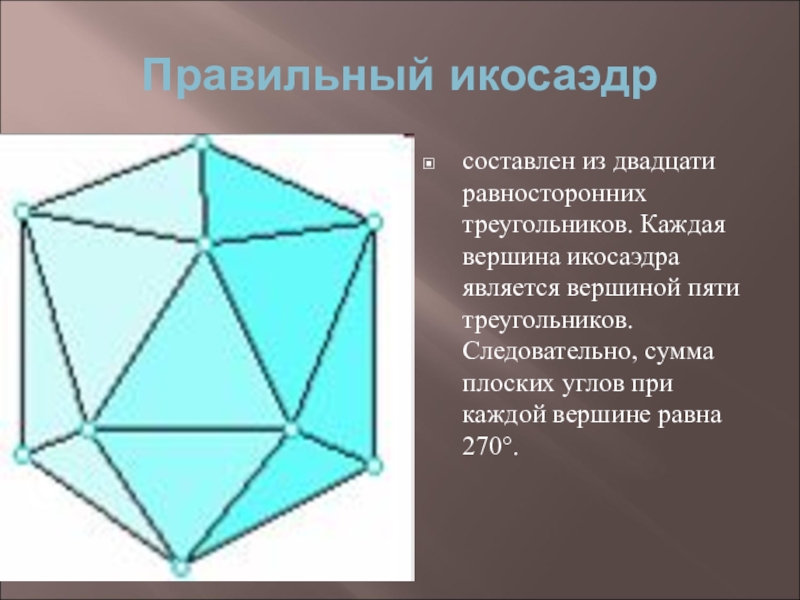
- 21. Правильный икосаэдрсоставлен из двадцати равносторонних треугольников. Каждая
- 22. Элементы симметрии: Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.
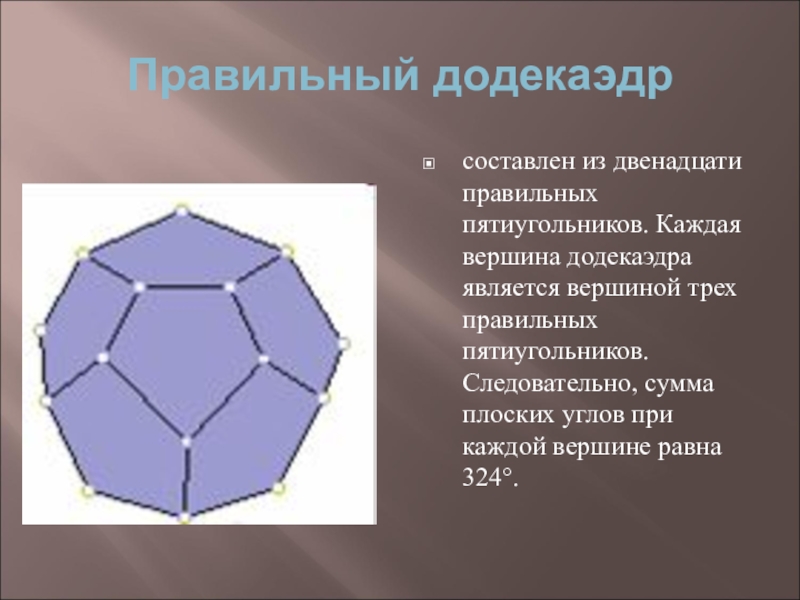
- 23. Правильный додекаэдрсоставлен из двенадцати правильных пятиугольников. Каждая
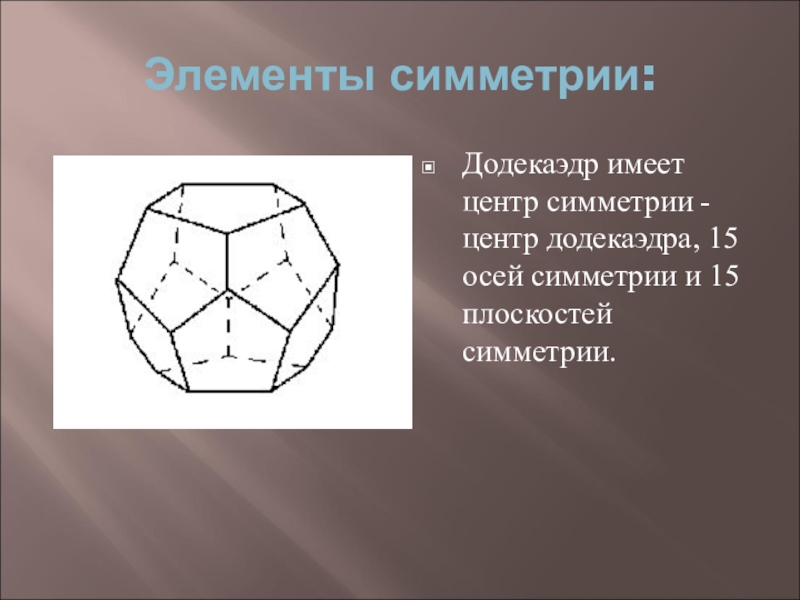
- 24. Элементы симметрии: Додекаэдр имеет центр симметрии -
- 25. "Тайная вечеря" С. Дали
- 26. А. Дюрер. Меланхолия. Фрагмент гравюры
- 27. Домашнее задание: п. 31 – 32, № 271 – 275 (любой на выбор).
Симметрия … есть идея,с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство Г. Вейль
Слайд 2Симметрия … есть идея,
с помощью которой человек
веками пытается объяснить
и
создать порядок,
красоту и совершенство
красоту и совершенство
Г. Вейль
Слайд 3Что такое симметрия?
Симметрия в переводе с греческого означает соразмерность. Под симметрией
принято понимать свойство геометрической фигуры, расположенной в пространстве или на плоскости, заключающееся в закономерном повторении равных ее частей.
Две точки называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Две точки называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Слайд 7СИММЕТРИЯ В ПРОСТРАНСТВЕ
«Что может быть более похоже на мою
руку
или мое ухо, чем их собственное
отражение в зеркале? И все же руку,
которую я вижу в зеркале, нельзя поставить
на место постоянной руки…»
Иммануил Кант
отражение в зеркале? И все же руку,
которую я вижу в зеркале, нельзя поставить
на место постоянной руки…»
Иммануил Кант
Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка плоскости считается симметричной самой себе.
Слайд 8СИММЕТРИЯ В ПРОСТРАНСТВЕ
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии
фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.
Слайд 12Многие атомы в пространстве располагаются по принципу симметрии
Кристаллы блещут симметрией
Е. С. Федоров
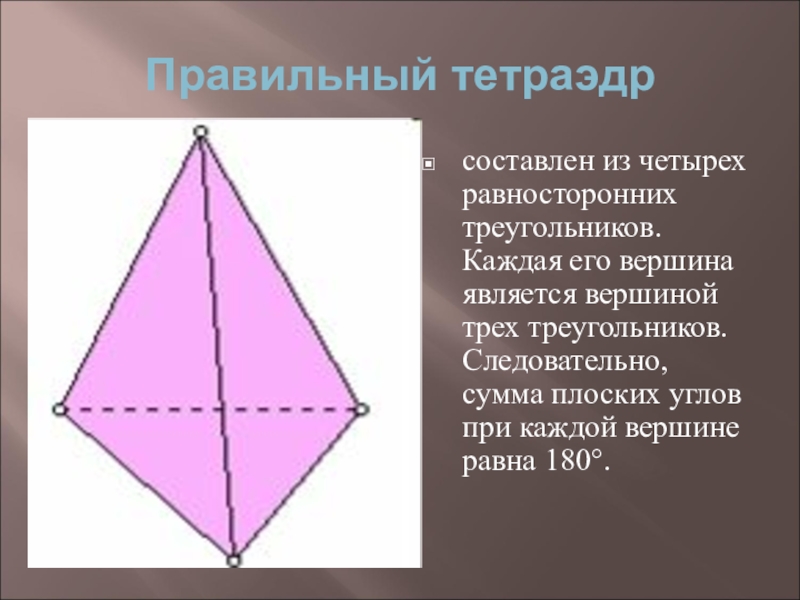
Слайд 15Правильный тетраэдр
составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной
трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
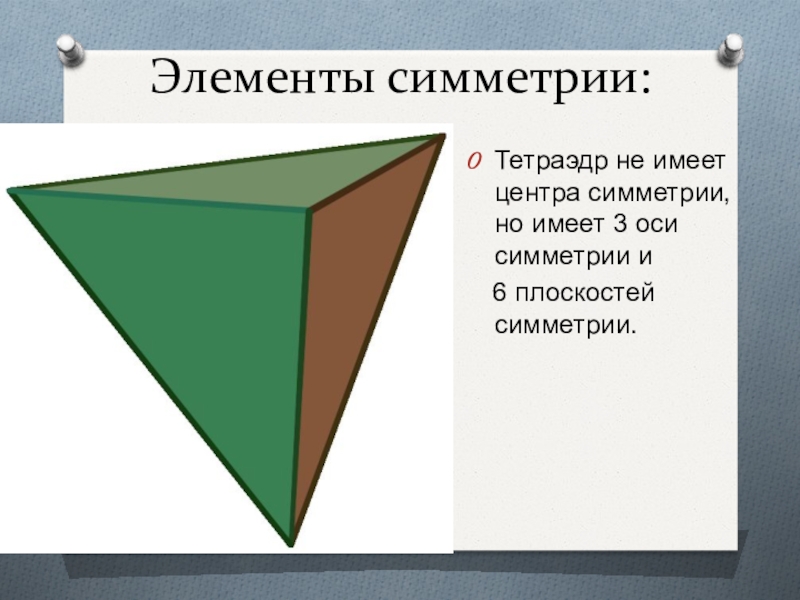
Слайд 16Элементы симметрии:
Тетраэдр не имеет центра симметрии, но имеет 3 оси
симметрии и
6 плоскостей симметрии.
6 плоскостей симметрии.
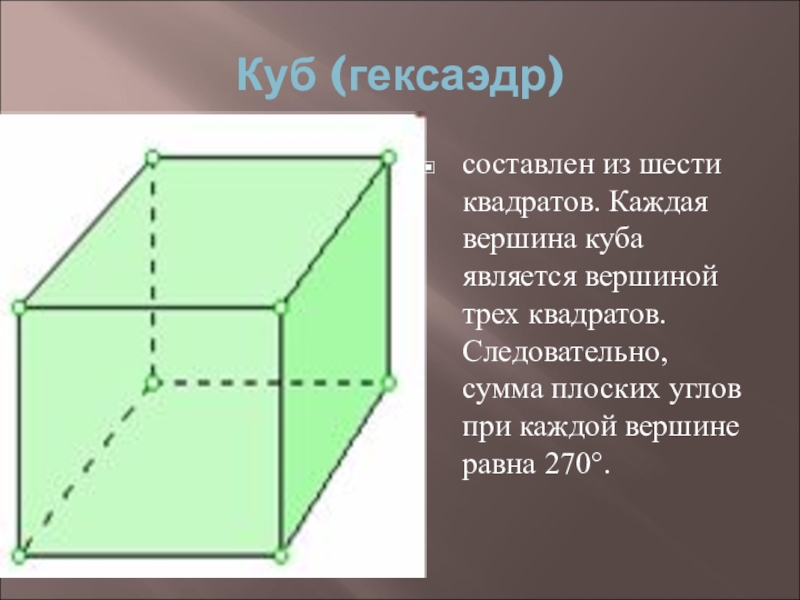
Слайд 17Куб (гексаэдр)
составлен из шести квадратов. Каждая вершина куба является вершиной трех
квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270°.
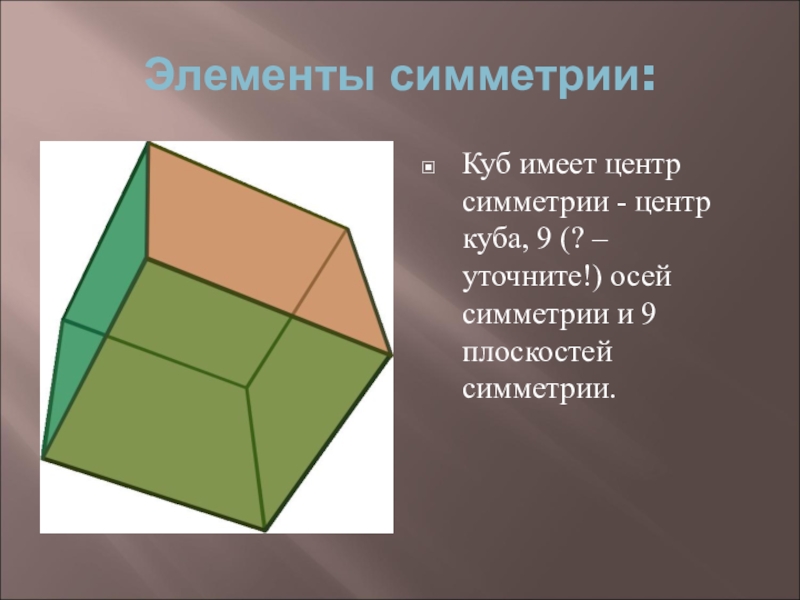
Слайд 18Элементы симметрии:
Куб имеет центр симметрии - центр куба, 9 (?
– уточните!) осей симметрии и 9 плоскостей симметрии.
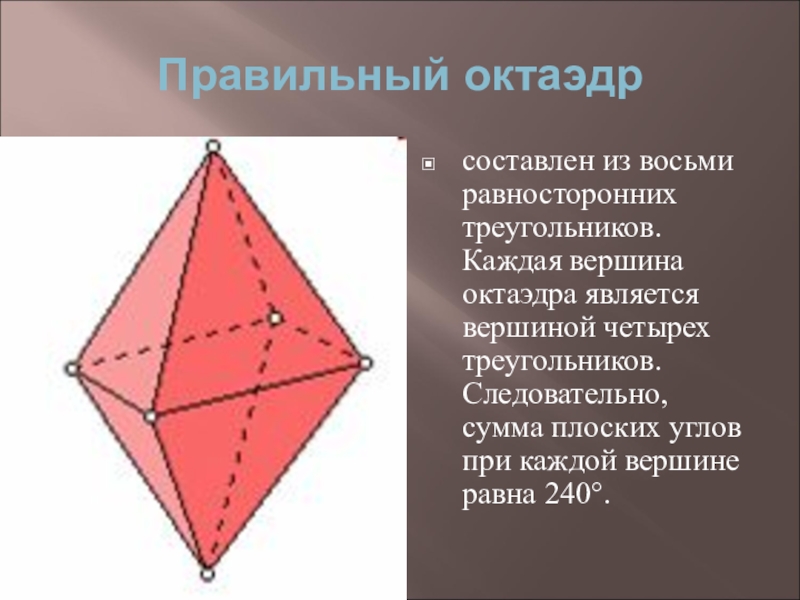
Слайд 19Правильный октаэдр
составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной
четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.
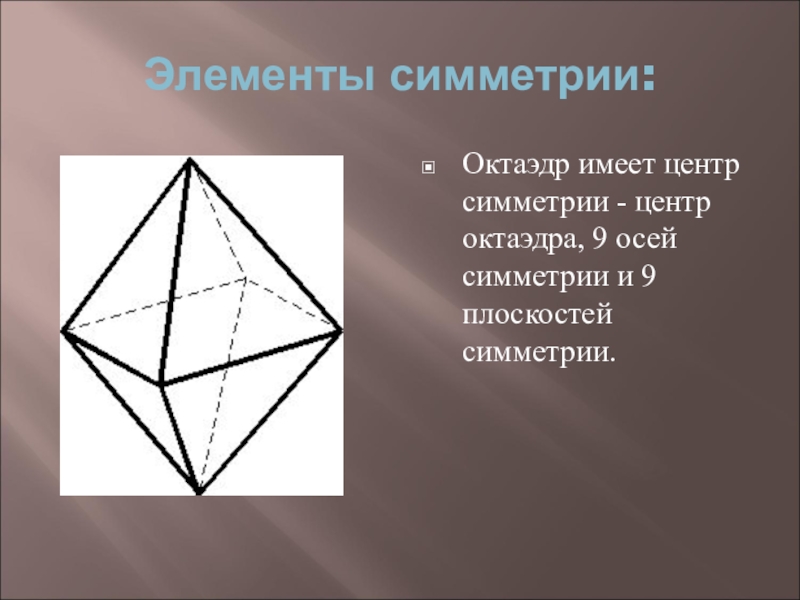
Слайд 20Элементы симметрии:
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей
симметрии и 9 плоскостей симметрии.
Слайд 21Правильный икосаэдр
составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной
пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 270°.
Слайд 22Элементы симметрии:
Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей
симметрии и 15 плоскостей симметрии.
Слайд 23Правильный додекаэдр
составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной
трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.
Слайд 24Элементы симметрии:
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей
симметрии и 15 плоскостей симметрии.