- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку математики Начальные геометрические сведения
Содержание
- 1. Презентация к уроку математики Начальные геометрические сведения
- 2. Периоды развития математикиPазвитие математики началось примерно в
- 3. Необходимость возникновения науки Геометрия возникла в результате практической
- 4. Зарождение науки ЕгипетДревнеегипетские математические тексты относятся к
- 5. Иероглифическая запись уравнения
- 6. ВавилонВавилоняне писали клинописными значками на глиняных табличках,
- 7. Вавилонские цифры
- 8. Древняя ГрецияМатематика в современном понимании этого слова
- 9. Греческие цифры
- 10. Период элементарной математикиВозникает математика как самостоятельная наука
- 11. Период создания математики
- 12. Современная математикаСложился стандарт требований к логической строгости.
- 13. Что такое геометрия? Геометрия – самостоятельная наука, занимающаяся изучением геометрических фигур.
- 14. В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета.
- 15. За несколько столетий до нашей эры в
- 16. Первым, кто начал получать новые геометрические факты
- 17. Фалес Милетский Oснователь милетской школы, один из легендарных
- 18. Наибольшее влияние на всё последующее развитие геометрии
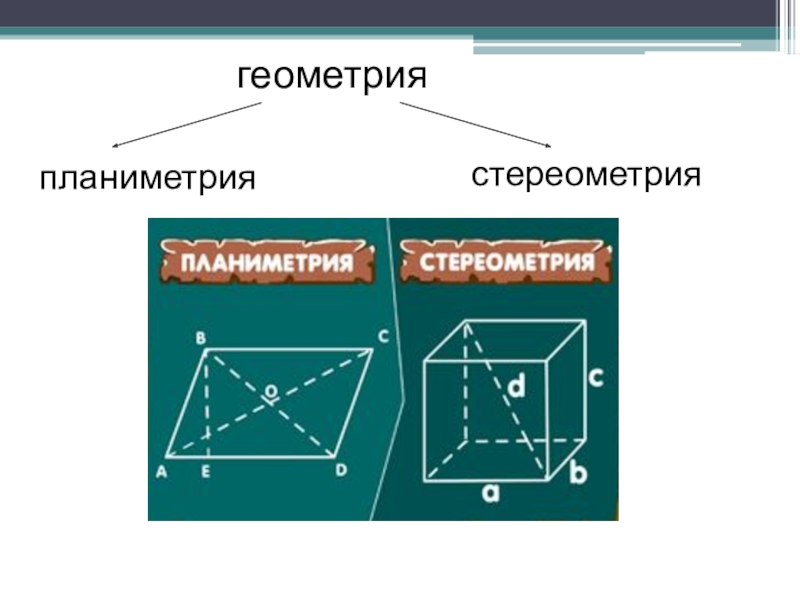
- 19. геометрияпланиметриястереометрия
- 20. Планиметрия – раздел геометрии, изучающий свойства фигур
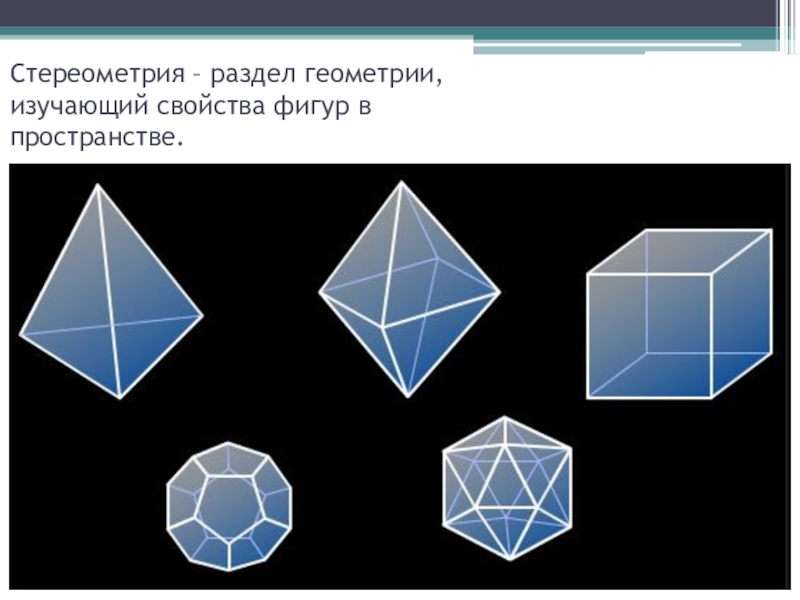
- 21. Стереометрия – раздел геометрии, изучающий свойства фигур в пространстве.
Периоды развития математикиPазвитие математики началось примерно в 3000 до н.э. благодаря вавилонянам,египтянам и грекам.Период зарождения математики Период элементарной математики (6-5 вв. до н.э. – 17 в. н.э.) Период математики переменных величин (17-18 вв.) Период современной математики(с
Слайд 1История возникновения геометрии
Подготовила учитель математики ГБОУ «Шебекинская гимназия-интернат» Клевцова С.В.
Слайд 2Периоды развития математики
Pазвитие математики началось примерно в 3000 до н.э. благодаря
вавилонянам,египтянам и грекам.
Период зарождения математики
Период элементарной математики (6-5 вв. до н.э. – 17 в. н.э.)
Период математики переменных величин (17-18 вв.)
Период современной математики(с 19 в. до наших дней)
Слайд 3Необходимость возникновения науки
Геометрия возникла в результате практической деятельности людей: нужно было
сооружать жилища, храмы, проводить дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры. Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни.
Слайд 4Зарождение науки
Египет
Древнеегипетские математические тексты относятся к началу II тысячелетия до н. э.
Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве домов, плотин, каналов и военных укреплений.
Основные сохранившиеся источники: папирус Ахмеса, он же папирус Ринда (84 математические задачи), и московский папирус Голенищева (25 задач).
Основные сохранившиеся источники: папирус Ахмеса, он же папирус Ринда (84 математические задачи), и московский папирус Голенищева (25 задач).
Слайд 6Вавилон
Вавилоняне писали клинописными значками на глиняных табличках, которые дошли до наших
дней (более 500000, из них около 400 связаны с математикой). Поэтому мы имеем довольно полное представление о математических достижениях учёных Вавилонского государства. Отметим, что корни культуры вавилонян были в значительной степени унаследованы от шумеров — клинописное письмо, счётная методика и т. п.
Слайд 8Древняя Греция
Математика в современном понимании этого слова родилась в Греции.
Во-первых,
пифагорейская школа выдвинула тезис «Числа правят миром».
Во-вторых, для открытия таких истин пифагорейцы разработали законченную методологию. Сначала они составили список первичных, интуитивно очевидных математических истин (аксиомы, постулаты). Затем с помощью логических рассуждений из этих истин выводились новые утверждения, которые также обязаны быть истинными. Так появилась дедуктивная математика.
Греки проверили справедливость этого тезиса во многих областях: астрономия, оптика, музыка, геометрия, позже — механика.
Во-вторых, для открытия таких истин пифагорейцы разработали законченную методологию. Сначала они составили список первичных, интуитивно очевидных математических истин (аксиомы, постулаты). Затем с помощью логических рассуждений из этих истин выводились новые утверждения, которые также обязаны быть истинными. Так появилась дедуктивная математика.
Греки проверили справедливость этого тезиса во многих областях: астрономия, оптика, музыка, геометрия, позже — механика.
Слайд 10Период элементарной математики
Возникает математика как самостоятельная наука с ясным пониманием своеобразия
её метода и необходимости систематического развития ее основных понятий и предложений в общей форме.
Из арифметики постепенно вырастает теория чисел. Создаётся систематическое учение о величинах и измерении.
Из арифметики постепенно вырастает теория чисел. Создаётся систематическое учение о величинах и измерении.
Слайд 11Период создания математики переменных величин
На первый план
выдвигается понятие функции.
Изучение переменных величин и функциональных зависимостей приводит к основным понятиям математического анализа, вводящим в математике в явном виде идею бесконечного, к понятиям предела, производной, дифференциала и интеграла, созданию аналитический геометрии.
Наряду с уравнениями, в которых неизвестными являются числа, появляются уравнения, в которых неизвестны и подлежат определению функции.
Изучение переменных величин и функциональных зависимостей приводит к основным понятиям математического анализа, вводящим в математике в явном виде идею бесконечного, к понятиям предела, производной, дифференциала и интеграла, созданию аналитический геометрии.
Наряду с уравнениями, в которых неизвестными являются числа, появляются уравнения, в которых неизвестны и подлежат определению функции.
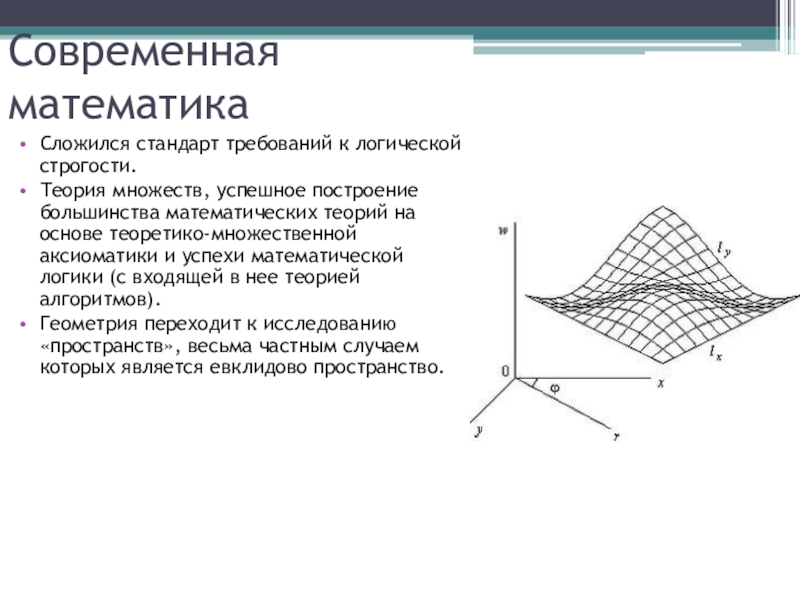
Слайд 12Современная математика
Сложился стандарт требований к логической строгости.
Теория множеств, успешное построение
большинства математических теорий на основе теоретико-множественной аксиоматики и успехи математической логики (с входящей в нее теорией алгоритмов).
Геометрия переходит к исследованию «пространств», весьма частным случаем которых является евклидово пространство.
Геометрия переходит к исследованию «пространств», весьма частным случаем которых является евклидово пространство.
Слайд 13Что такое геометрия?
Геометрия – самостоятельная наука, занимающаяся изучением геометрических фигур.
Слайд 14 В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их
других свойств: массы, цвета.
Слайд 15 За несколько столетий до нашей эры в Вавилоне, Китае и Греции
уже существовали начальные геометрические знания, которые добывались опытным путём. Знания не были ещё систематизированы и передавались от поколения к поколению в виде правил и рецептов.
Например, правил нахождения площадей фигур, объёмов тел, построения прямых углов и т.д.
Не было ещё доказательств этих правил, и их изложение не представляло собой научной теории.
Например, правил нахождения площадей фигур, объёмов тел, построения прямых углов и т.д.
Не было ещё доказательств этих правил, и их изложение не представляло собой научной теории.
Слайд 16 Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств),
был древнегреческий математик Фалес (VI век до нашей эры).
Слайд 17Фалес Милетский
Oснователь милетской школы, один из легендарных "семи мудрецов". Происходил из
аристократического рода, был связан с храмом Аполлона Дидимского, патрона морской колонизации. Имя Фалеса уже в V в. стало нарицательным для мудреца. Считается, что Фалес ввел в употребление новое созвездие - Малую Медведицу.
Фалеса называют одним из первых греческих мыслителей, кто понял важность астрологии как науки. В историю вошло "затмение Фалеса " 28 мая 585 г. до н.э., предсказанное им за 6 лет до события (некоторые ученые считают это легендой, доказывая, что уровень развития науки во времена Фалеса еще не позволял предсказывать затмения). В честь Фалеса названа малая планета 6001 Thales.
Фалеса называют одним из первых греческих мыслителей, кто понял важность астрологии как науки. В историю вошло "затмение Фалеса " 28 мая 585 г. до н.э., предсказанное им за 6 лет до события (некоторые ученые считают это легендой, доказывая, что уровень развития науки во времена Фалеса еще не позволял предсказывать затмения). В честь Фалеса названа малая планета 6001 Thales.
Слайд 18 Наибольшее влияние на всё последующее развитие геометрии оказали труды греческого учёного
Евклида, жившего в Александрии в III веке до нашей эры.
Слайд 20Планиметрия – раздел геометрии, изучающий свойства фигур на плоскости (от латинского
слова «планум» - плоскость и греческого «метрео» - измеряю).