- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 8 классе по теме Параллелограмм
Содержание
- 1. Презентация к уроку геометрии в 8 классе по теме Параллелограмм
- 2. ABCD – параллелограмм. AB II CD, DC
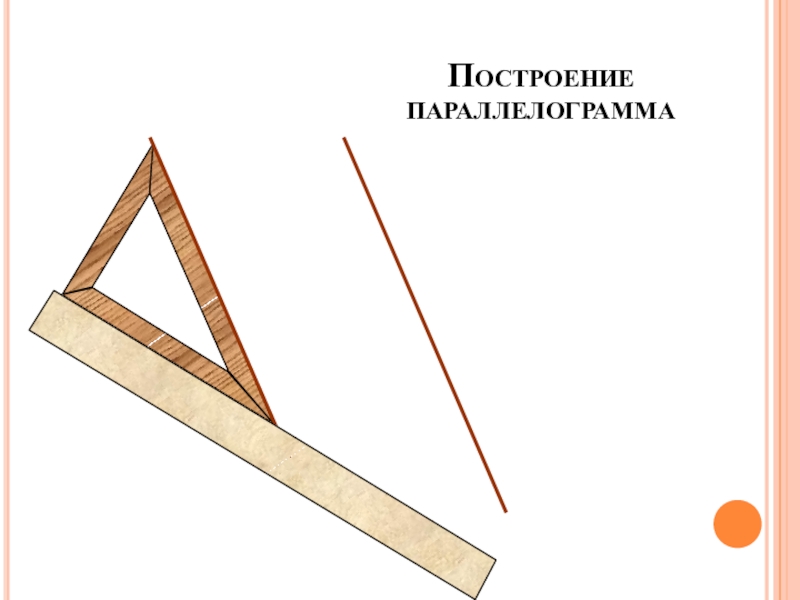
- 3. Построение параллелограмма
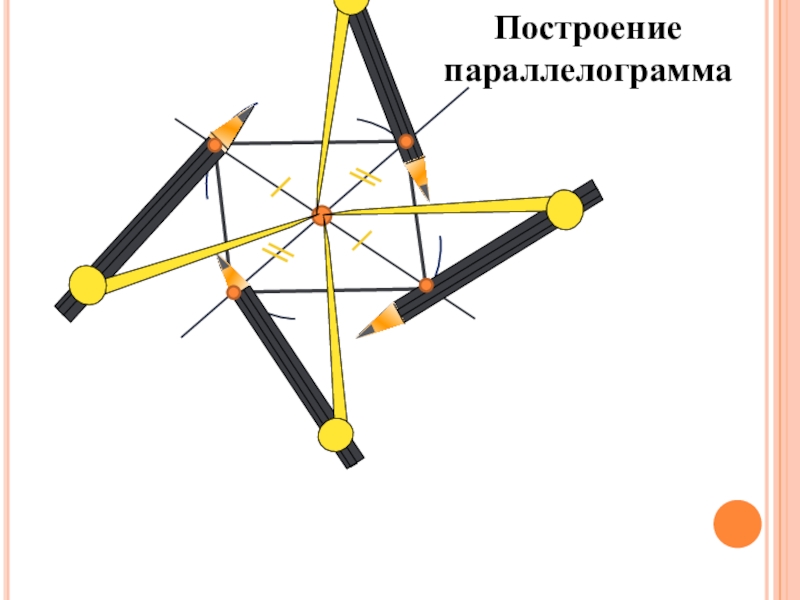
- 4. Построение параллелограмма
- 5. Свойства параллелограммаВ параллелограмме противоположные стороны равны и
- 6. Свойство 1. В параллелограмме противоположные
- 7. Свойства параллелограммаДиагонали параллелограмма делятся точкой пересечения пополамОВО = ОD, АО = ОСО – точка пересечения диагоналей
- 8. Свойство 2. Диагонали параллелограмма точкой
- 9. Свойства параллелограммаВ параллелограмме сумма углов, прилежащих к
- 10. Признаки параллелограммаЕсли в четырехугольнике две стороны равны
- 11. ДоказательствоПусть АВ = СD и АВ ∥
- 12. Признаки параллелограммаЕсли в четырехугольнике противоположные стороны попарно
- 13. АВСD- четырехугольник, АВ = CD, ВС =
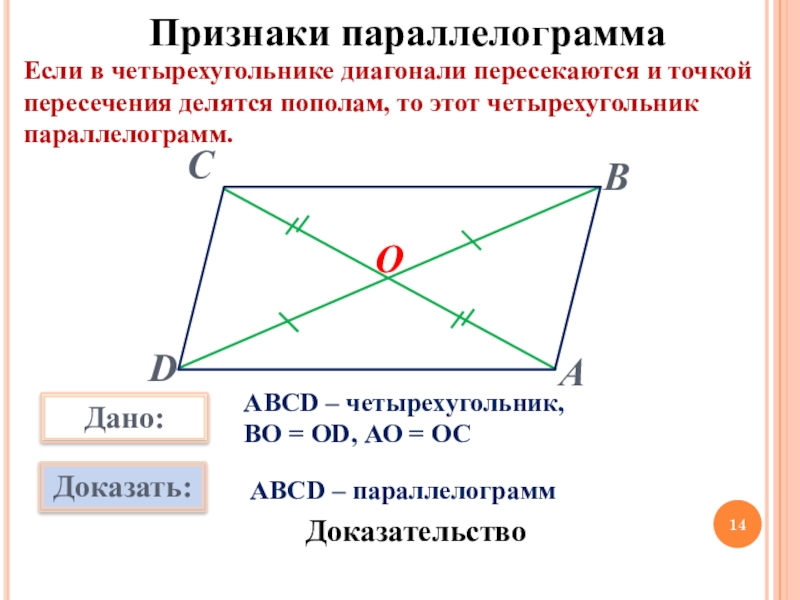
- 14. ОПризнаки параллелограммаЕсли в четырехугольнике диагонали пересекаются и
- 15. ОАВСD – четырехугольник, ВО = ОD, АО
- 16. АВСD – четырехугольник, ∠BАC = ∠ACD, ∠CAD
Слайд 1Урок геометрии
в 8 классе по теме «Параллелограмм»
Подготовила: Богданова Ольга Николаевна,
учитель математики
МКОУ «Овечкинская СОШ
Завьяловского района»
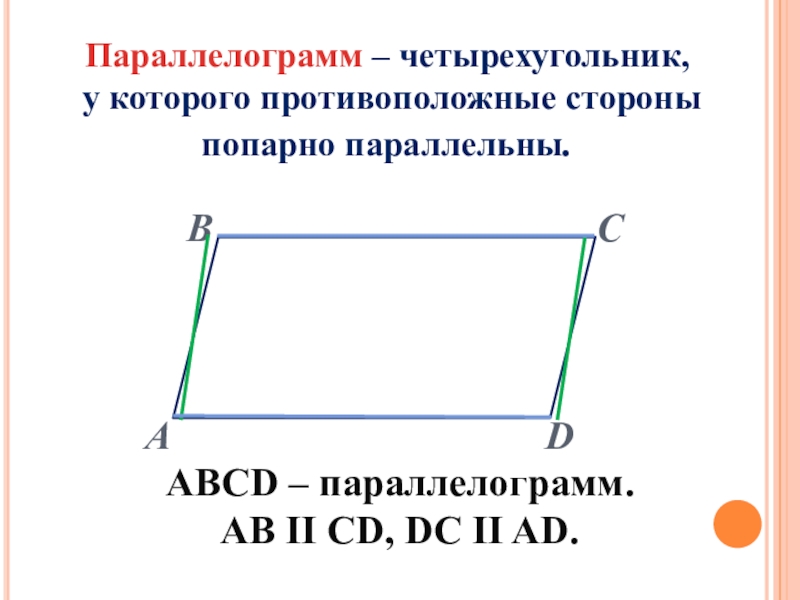
Слайд 2ABCD – параллелограмм.
AB II CD, DC II AD.
Параллелограмм – четырехугольник,
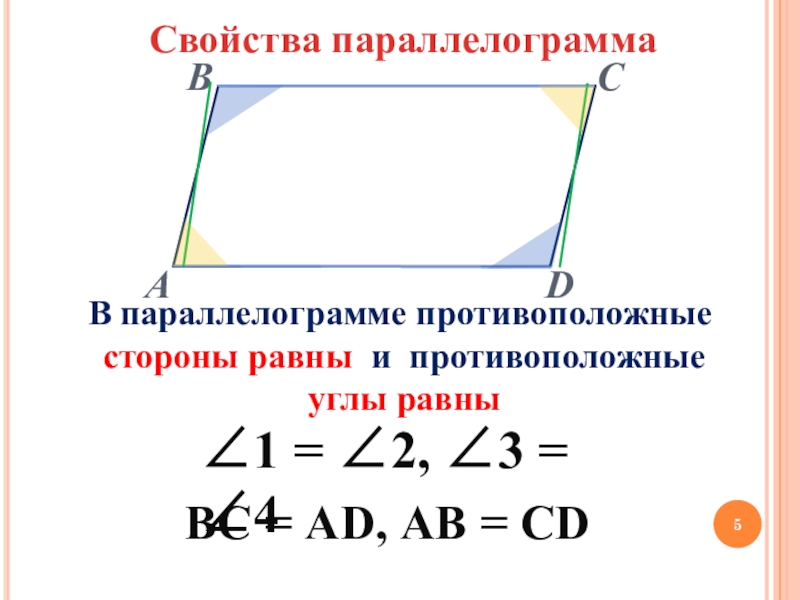
Слайд 5Свойства параллелограмма
В параллелограмме противоположные
стороны равны и противоположные
углы
∠1 = ∠2, ∠3 = ∠4
ВС = AD, АВ = СD
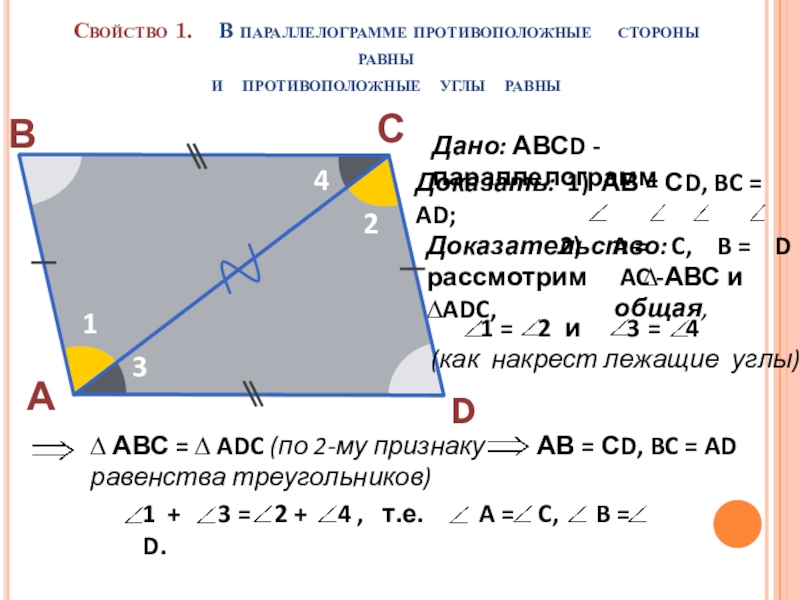
Слайд 6Свойство 1. В параллелограмме противоположные стороны равны и
А
В
С
D
Дано: АВСD - параллелограмм
Доказательство: рассмотрим ∆ АВС и ∆ADC,
AC - общая,
1
2
3
4
АВ = СD, BC = AD
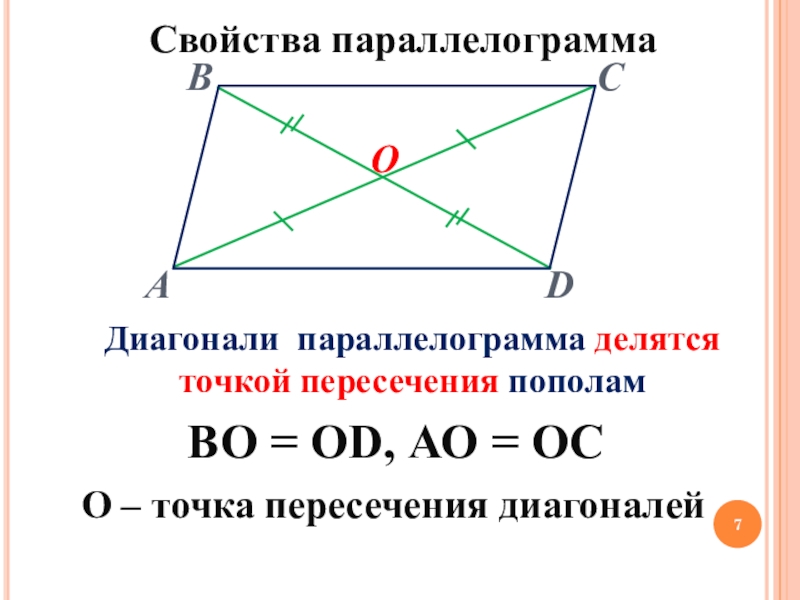
Слайд 7Свойства параллелограмма
Диагонали параллелограмма делятся точкой пересечения пополам
О
ВО = ОD, АО =
О – точка пересечения диагоналей
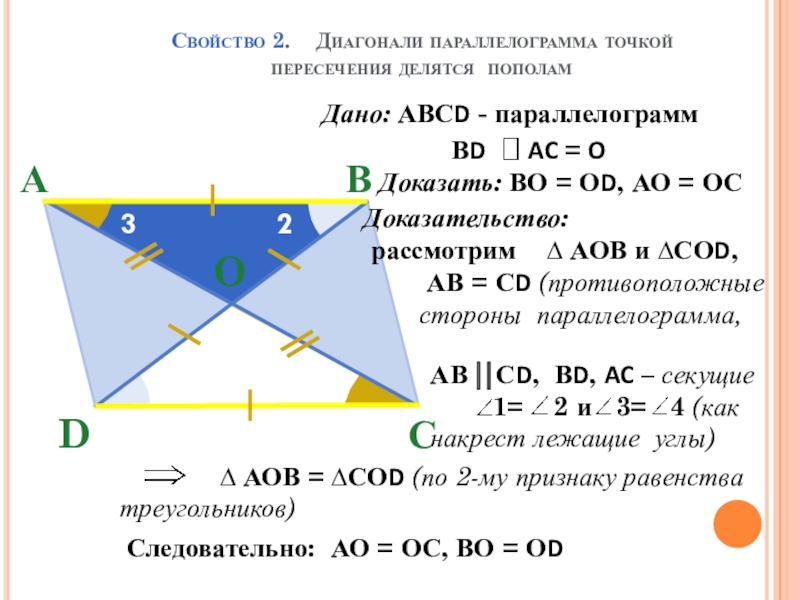
Слайд 8Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам
В
А
С
D
1
3
4
Дано: АВСD
Доказать: ВО = ОD, АО = ОС
Доказательство:
рассмотрим ∆ АОВ и ∆СОD,
Следовательно: АО = ОС, ВО = ОD
O
АВ = СD (противоположные стороны параллелограмма,
2
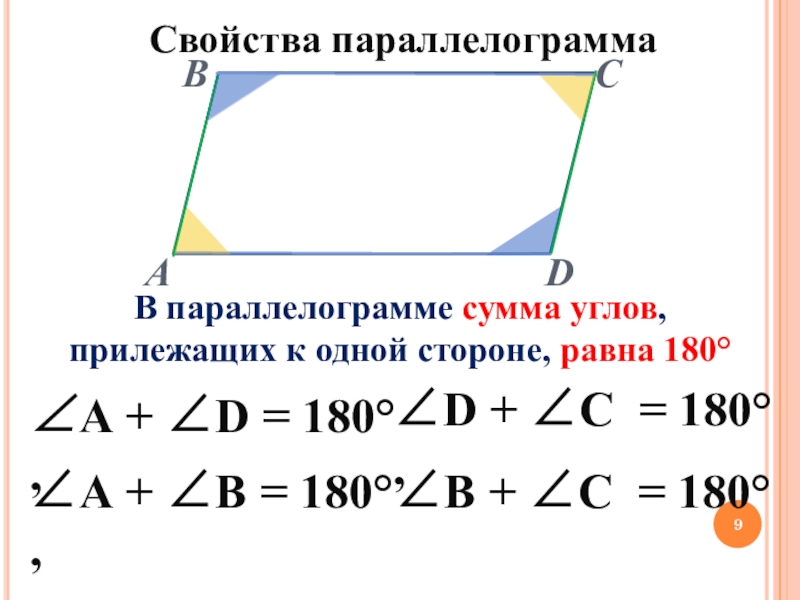
Слайд 9Свойства параллелограмма
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°
∠А
∠D + ∠C = 180° ,
∠А + ∠B = 180° ,
∠В + ∠C = 180°
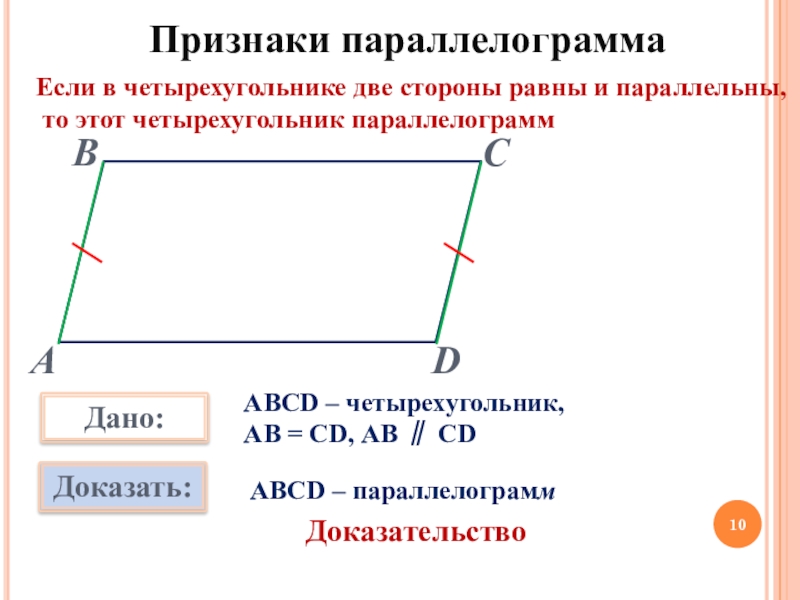
Слайд 10Признаки параллелограмма
Если в четырехугольнике две стороны равны и параллельны,
то
АВСD – четырехугольник,
АВ = CD, АВ ∥ CD
АВСD – параллелограмм
Доказательство
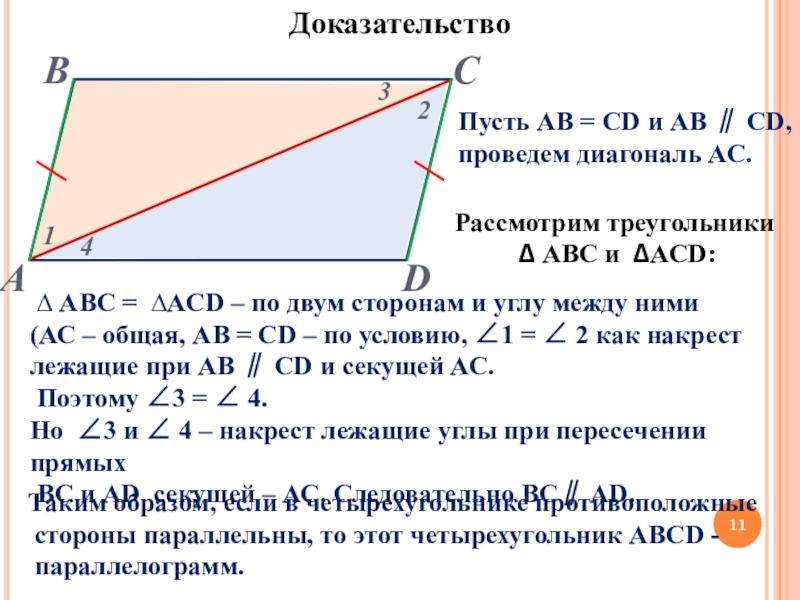
Слайд 11Доказательство
Пусть АВ = СD и АВ ∥ СD,
проведем диагональ АС.
Рассмотрим
∆ АBC и ∆ACD:
∆ АBC = ∆ACD – по двум сторонам и углу между ними
(АС – общая, АВ = СD – по условию, ∠1 = ∠ 2 как накрест лежащие при АВ ∥ СD и секущей АС.
Поэтому ∠3 = ∠ 4.
1
2
3
4
Но ∠3 и ∠ 4 – накрест лежащие углы при пересечении прямых
ВС и AD секущей – АС. Следовательно ВС∥ AD.
Таким образом, если в четырехугольнике противоположные
стороны параллельны, то этот четырехугольник АВСD -
параллелограмм.
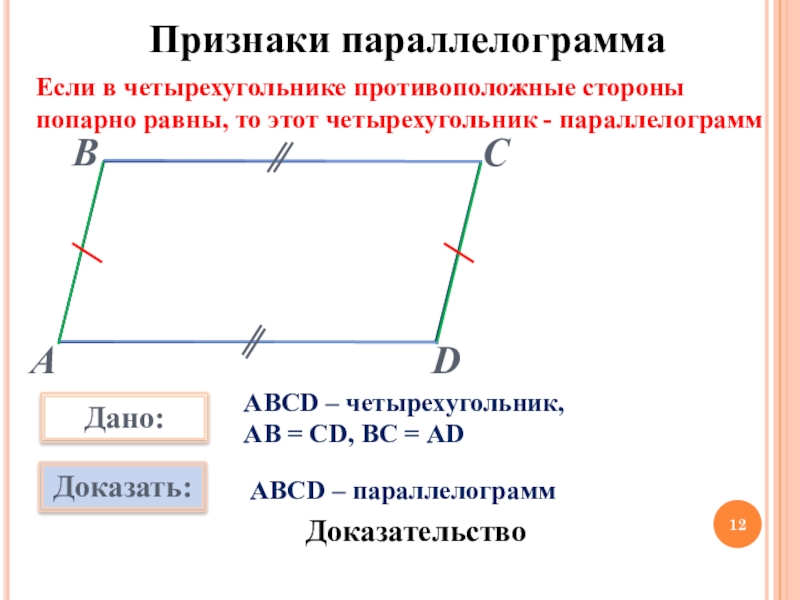
Слайд 12Признаки параллелограмма
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник
АВСD – четырехугольник,
АВ = CD, ВС = АD
АВСD – параллелограмм
Доказательство
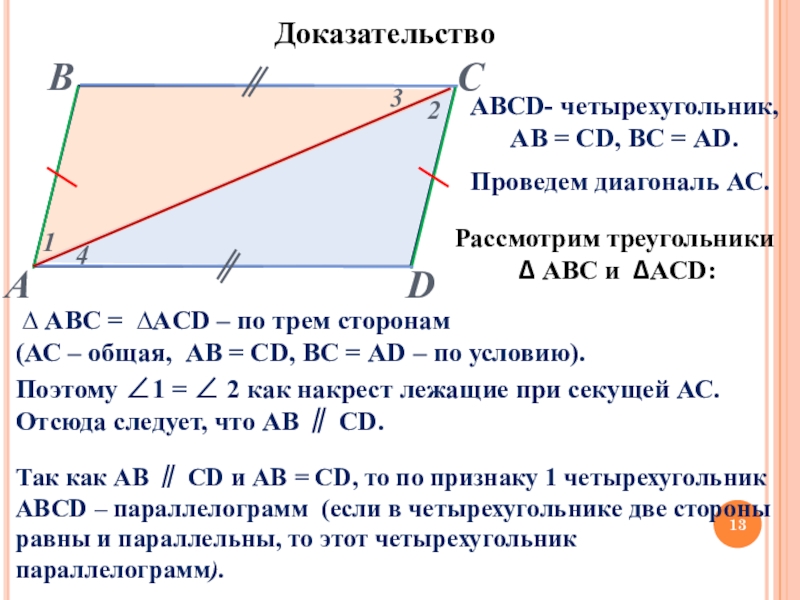
Слайд 13АВСD- четырехугольник,
АВ = CD, ВС = АD.
Доказательство
Рассмотрим треугольники
∆
∆ АBC = ∆ACD – по трем сторонам
(АС – общая, АВ = СD, ВС = АD – по условию).
Поэтому ∠1 = ∠ 2 как накрест лежащие при секущей АС.
Отсюда следует, что АВ ∥ СD.
Проведем диагональ АС.
Так как АВ ∥ СD и АВ = СD, то по признаку 1 четырехугольник АВСD – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).
Слайд 14О
Признаки параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам,
АВСD – четырехугольник,
ВО = ОD, АО = ОС
АВСD – параллелограмм
Доказательство
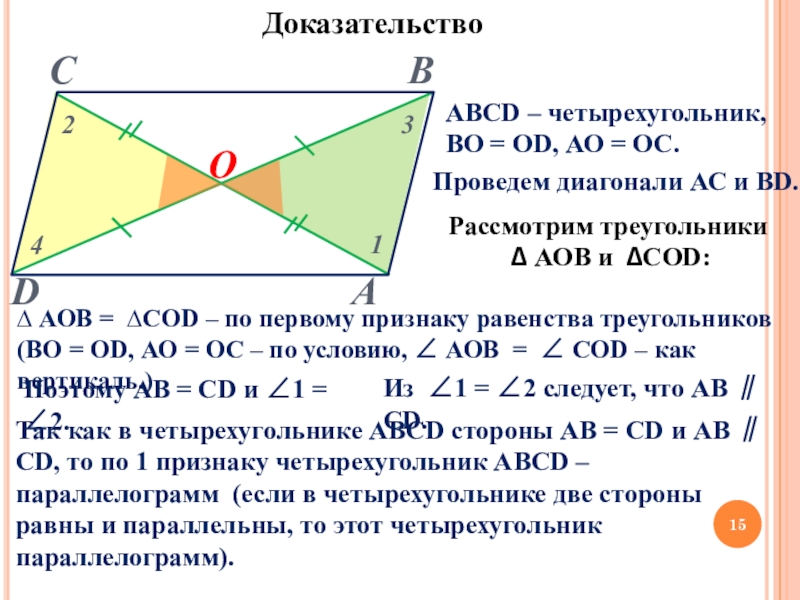
Слайд 15О
АВСD – четырехугольник,
ВО = ОD, АО = ОС.
Доказательство
Проведем диагонали АС
Рассмотрим треугольники
∆ АОB и ∆CОD:
∆ АОB = ∆CОD – по первому признаку равенства треугольников
(ВО = ОD, АО = ОС – по условию, ∠ АОB = ∠ CОD – как вертикаль.)
Поэтому АВ = CD и ∠1 = ∠2.
Из ∠1 = ∠2 следует, что АВ ∥ CD.
Так как в четырехугольнике АВСD стороны АВ = CD и АВ ∥ CD, то по 1 признаку четырехугольник АВСD – параллелограмм (если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник параллелограмм).
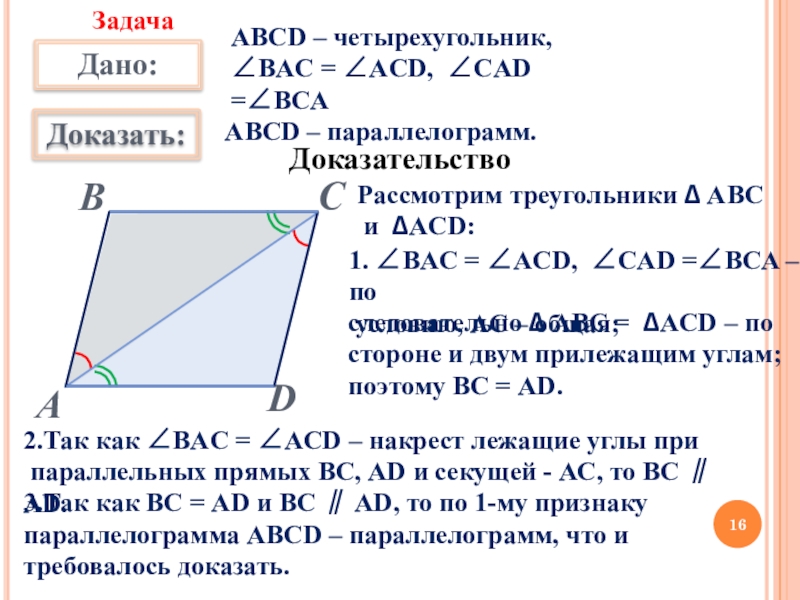
Слайд 16АВСD – четырехугольник,
∠BАC = ∠ACD, ∠CAD =∠BCA
АВСD – параллелограмм.
Доказательство
Рассмотрим треугольники
и ∆ACD:
1. ∠BАC = ∠ACD, ∠CAD =∠BCA – по
условию, АС – общая;
следовательно ∆ АBC = ∆ACD – по
стороне и двум прилежащим углам;
поэтому ВС = AD.
2.Так как ∠BАC = ∠ACD – накрест лежащие углы при
параллельных прямых ВС, AD и секущей - АС, то ВС ∥ AD.
3.Так как ВС = AD и ВС ∥ AD, то по 1-му признаку параллелограмма АВСD – параллелограмм, что и требовалось доказать.
Задача