- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 8 классе по теме Теорема Пифагора
Содержание
- 1. Презентация к уроку геометрии в 8 классе по теме Теорема Пифагора
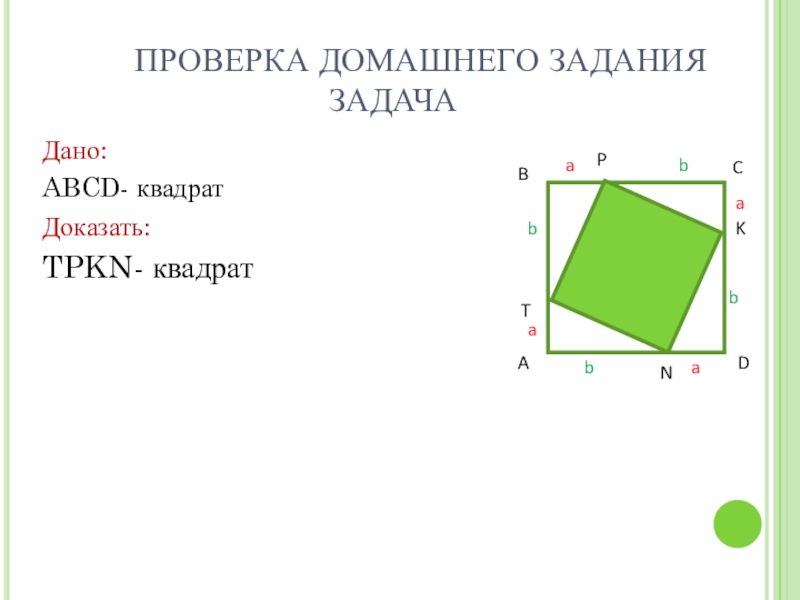
- 2. ПРОВЕРКА ДОМАШНЕГО
- 3. НГИПОТЕУЗАИАНФАФМСЕЛАТЕСТКМАТЕПИГРПСОУОМЯЬЛОГЙЫНЕННМолодцы!
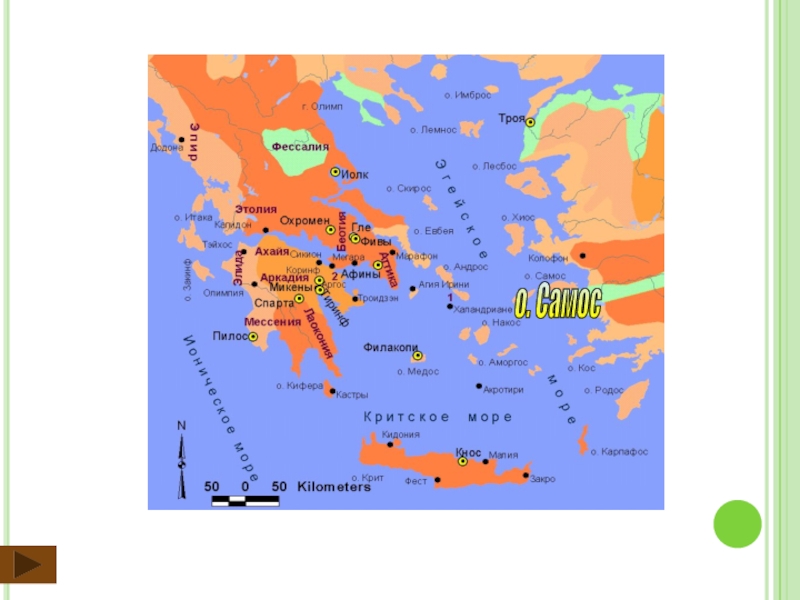
- 4. о. Самос
- 5. НЕМНОГО ИСТОРИИ… Пифагор Самосский ( 570—490 гг. до н. э.)
- 6. ПИФАГОРЕЙСКАЯ ШКОЛА
- 7. ОПОРНОЕ ПОВТОРЕНИЕ ПО ГОТОВЫМ ЧЕРТЕЖАМКакой треугольник изображён?
- 8. Задача: Для крепления мачты нужно установить 4
- 9. ТЕОРЕМА ПИФАГОРА
- 10. Геометрия обладает двумя великими сокровищами. Первое
- 11. ПРАКТИЧЕСКАЯ РАБОТА Измерьте катеты и
- 12. «Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик
- 13. ДОКАЗАТЕЛЬСТВО Достроим треугольник до квадрата
- 14. Из [1] и [2] получим(a+b)²=2ab+c²a²+ b²+2ab=2ab+c²a²+b²=c²Что и требовалось доказать.
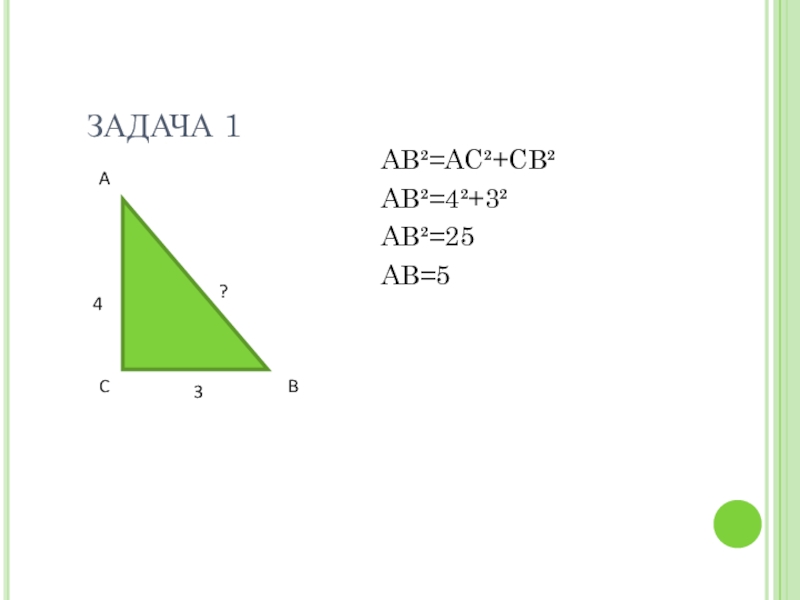
- 15. ЗАДАЧА 1AB²=AC²+CB²AB²=4²+3²AB²=25AB=543?ACB
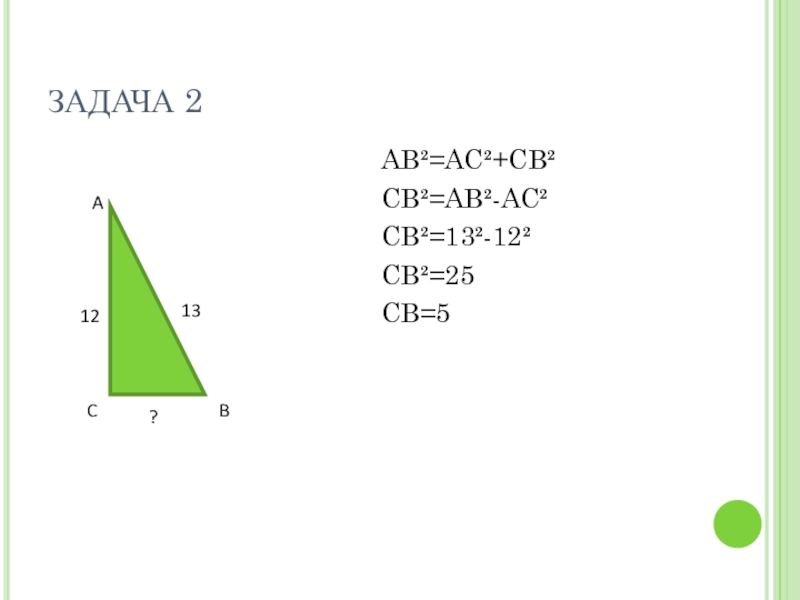
- 16. ЗАДАЧА 2AB²=AC²+CB²CB²=AB²-AC²CB²=13²-12²CB²=25CB=5ACB1312?
- 17. Если дан нам треугольникИ притом с прямым
- 18. АЛГОРИТМ НАХОЖДЕНИЯ НЕИЗВЕСТНОЙ СТОРОНЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
- 19. ЗАДАЧА ИНДИЙСКОГО МАТЕМАТИКА XII ВЕКА БХАСКАРЫНа
- 20. ЗАДАЧА ИЗ УЧЕБНИКА «АРИФМЕТИКА»
- 21. Слайд 21
- 22. РЕШЕНИЕ:Вариант 1.1)AB²=AC²+CB²AB²=20²+15²AB²=625AB=252) Тр.ACD-прямоуг.AC²=AD²+DC²AC²=4²+3²AC²=25AC=53)Тр.ABD прямоуг.AD²=AB²-BD²AD²=13²-12²AD²=25AD=5AC=2AD=2*5=10Вариант 21)AB²=AC²+CB²BC²=AB²-AC²BC²=10²-6²BC²=64BC=82) Тр.BAD- прямоуг.BA²=BD²-AD²BA²=10²-8²BA²=36BA=63)AD=½AC=10Тр.ABD прямоуг.AB²=AD²+BD²AB²=10²+24²AB²=676AB=26
- 23. ОТВЕТЫ К ТЕСТУ1) б2)а3) в4) б5) б
- 24. Художник Ф.А. Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу»
- 25. Суть истины вся в том,
- 26. Выберите одно из
- 27. Слайд 27
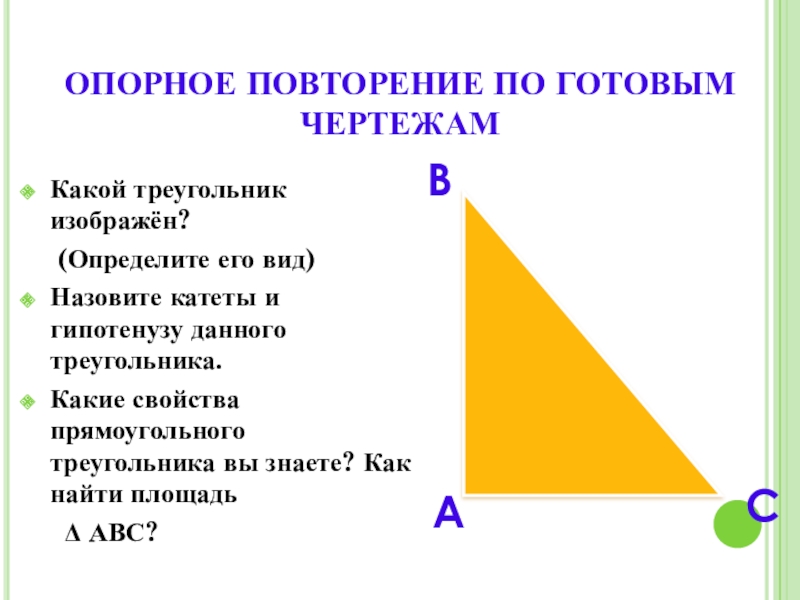
Слайд 7ОПОРНОЕ ПОВТОРЕНИЕ ПО ГОТОВЫМ ЧЕРТЕЖАМ
Какой треугольник изображён?
(Определите его
Назовите катеты и гипотенузу данного треугольника.
Какие свойства прямоугольного треугольника вы знаете? Как найти площадь
Δ АВС?
В
А
С
Слайд 8Задача:
Для крепления мачты нужно установить 4 троса. Один конец каждого
Слайд 10Геометрия обладает двумя
великими сокровищами.
Первое - это теорема Пифагора,
которую
Слайд 11
ПРАКТИЧЕСКАЯ РАБОТА
Измерьте катеты и гипотенузу лежащих на столе прямоугольных треугольников.
Возведите все результаты в квадрат, т. е. узнайте величины a2; b2; c2.Результаты запишите в таблицу 2.
3. Сделайте выводы.
Слайд 12
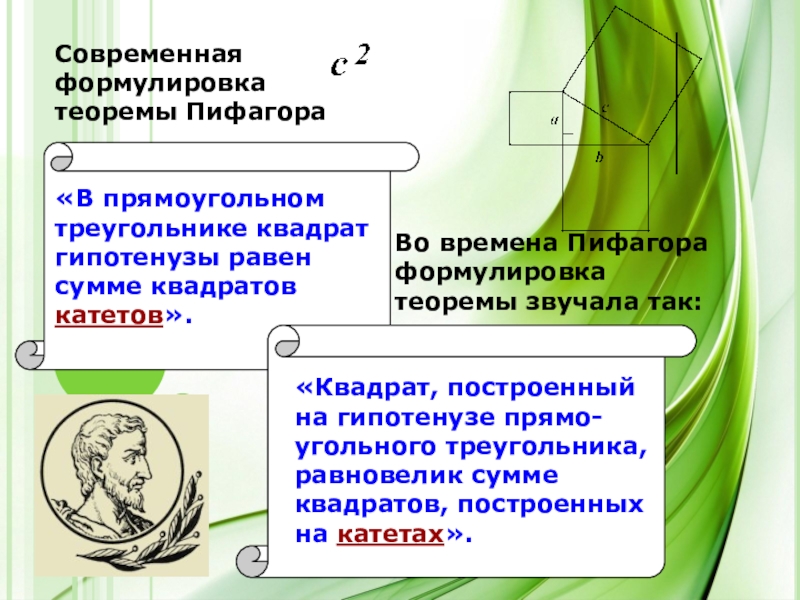
«Квадрат, построенный на гипотенузе прямо-угольного треугольника, равновелик сумме квадратов, построенных на
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов катетов».
Во времена Пифагора формулировка теоремы звучала так:
Современная формулировка
теоремы Пифагора
Слайд 13ДОКАЗАТЕЛЬСТВО
Достроим треугольник до квадрата со стороной a+b. Его
С другой стороны этот квадрат состоит из четырех равных треугольников
Sтр=1/2ab; 4Sтр=2ab
и квадрата со стороной с
Sкв=с²
Отсюда S=2ab+c² [2]
a
b
c
a
b
c
c
c
a
a
b
b
Слайд 17
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда
Катеты в квадрат возводим,
Сумму их легко находим –
И таким простым путём
К результату мы придём.
Слайд 19ЗАДАЧА ИНДИЙСКОГО МАТЕМАТИКА
XII ВЕКА БХАСКАРЫ
На берегу реки рос тополь одинокий.
Вдруг
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Слайд 20ЗАДАЧА ИЗ УЧЕБНИКА «АРИФМЕТИКА»
Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти.
Слайд 22РЕШЕНИЕ:
Вариант 1.
1)AB²=AC²+CB²
AB²=20²+15²
AB²=625
AB=25
2) Тр.ACD-прямоуг.
AC²=AD²+DC²
AC²=4²+3²
AC²=25
AC=5
3)Тр.ABD прямоуг.
AD²=AB²-BD²
AD²=13²-12²
AD²=25
AD=5
AC=2AD=2*5=10
Вариант 2
1)AB²=AC²+CB²
BC²=AB²-AC²
BC²=10²-6²
BC²=64
BC=8
2) Тр.BAD- прямоуг.
BA²=BD²-AD²
BA²=10²-8²
BA²=36
BA=6
3)AD=½AC=10
Тр.ABD прямоуг.
AB²=AD²+BD²
AB²=10²+24²
AB²=676
AB=26
Слайд 24
Художник Ф.А. Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу»
Слайд 25 Суть истины вся в том, что нам она -
А.Шамиссо
Слайд 26
Выберите одно из заданий:
1.Найдите другие доказательства теоремы
2.Найдите старинную задачу с использованием этой теоремы и решите её.
3.Приготовьте доклад о применении теоремы.
№ 483(б, в) ,№484(б)
Домашнее задание








![Презентация к уроку геометрии в 8 классе по теме Теорема Пифагора ДОКАЗАТЕЛЬСТВО Достроим треугольник до квадрата со стороной a+b. Его площадь ДОКАЗАТЕЛЬСТВО Достроим треугольник до квадрата со стороной a+b. Его площадь равна S=(a+b)²[1]С другой стороны этот](/img/thumbs/b6815933f53213f3cea00d067af3cf57-800x.jpg)
![Презентация к уроку геометрии в 8 классе по теме Теорема Пифагора Из [1] и [2] получим(a+b)²=2ab+c²a²+ b²+2ab=2ab+c²a²+b²=c²Что и требовалось доказать. Из [1] и [2] получим(a+b)²=2ab+c²a²+ b²+2ab=2ab+c²a²+b²=c²Что и требовалось доказать.](/img/thumbs/27f20a4920ddb59308fc088576f58b89-800x.jpg)