- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии по теме:Расстояния в пространстве(10класс)
Содержание
- 1. Презентация к уроку геометрии по теме:Расстояния в пространстве(10класс)
- 2. Расстояние между точками А и В
- 3. Расстояние от точки до прямой Расстоянием
- 4. Расстояние от точки до прямой можно вычислить:
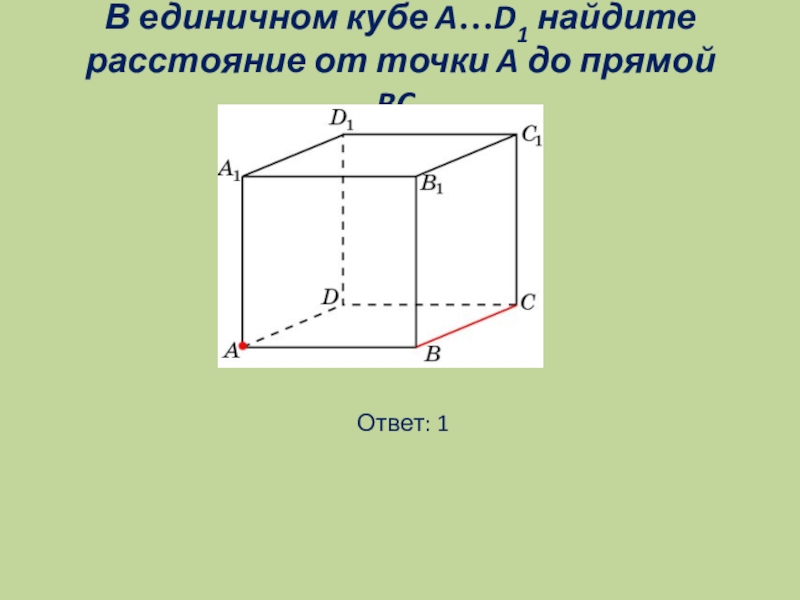
- 5. В единичном кубе A…D1 найдите расстояние от точки A до прямой BC. Ответ: 1
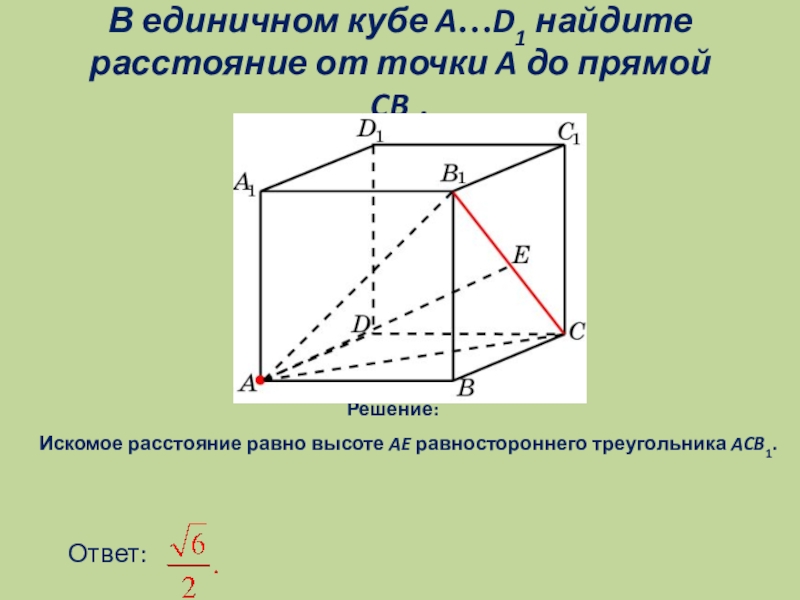
- 6. В единичном кубе A…D1 найдите расстояние от точки A до прямой CB1.
- 7. Задачи для самостоятельного решения 1)В правильной треугольной
- 8. Расстояние от точки до плоскостиРасстоянием от точки
- 9. • Расстояние от точки до плоскости, не
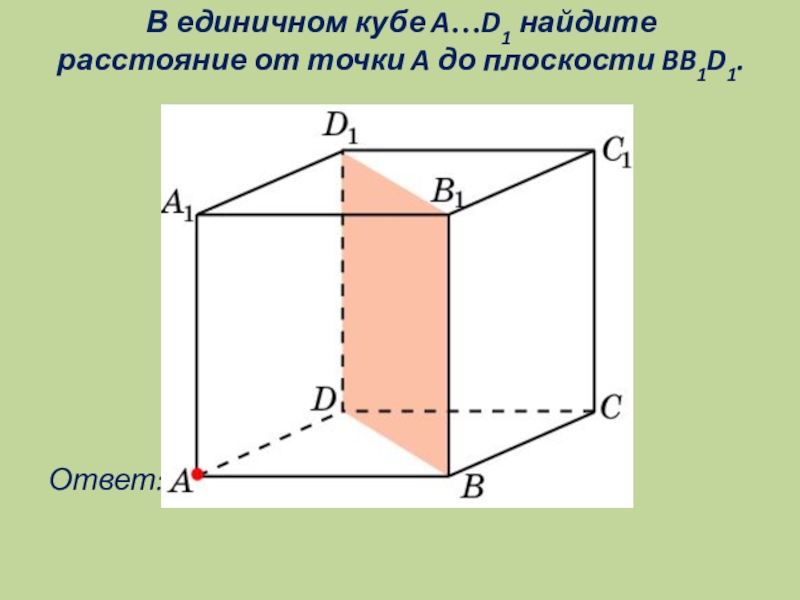
- 10. В единичном кубе A…D1 найдите расстояние от точки A до плоскости BB1D1. Ответ:√2/2
- 11. В правильной пирамиде SABCD, все ребра которой
- 12. Задачи для самостоятельного решения1.В правильном тетраэдре ABCD
- 13. Расстояние между скрещивающимися прямыми Расстоянием между
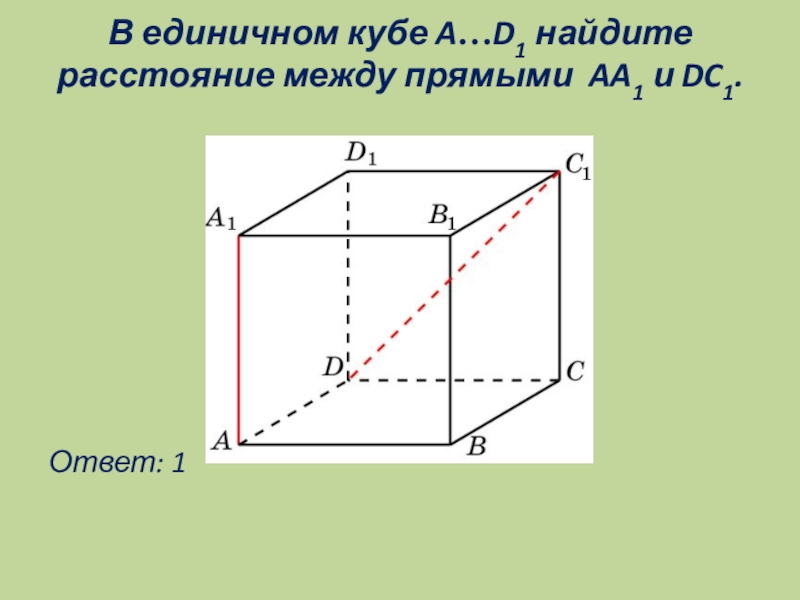
- 14. В единичном кубе A…D1 найдите расстояние между прямыми AA1 и DC1. Ответ: 1
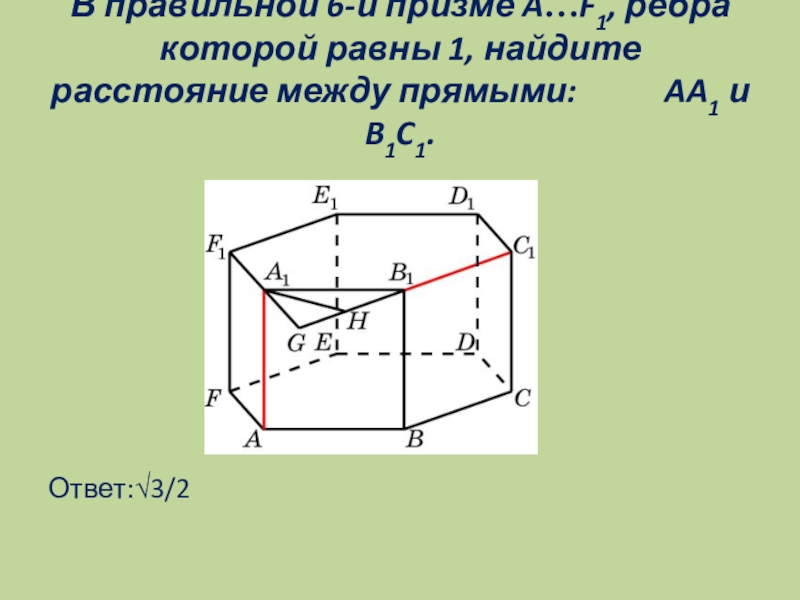
- 15. В правильной 6-й призме A…F1, ребра которой
- 16. Задачи для самостоятельного решения1.В правильной четырехугольной пирамиде
Расстояние между точками А и В можно вычислить: 1) как длину отрезка АВ, если отрезок АВ удается включить в некоторый треугольник в качестве одной из его сторон; 2) по формуле нахождения расстояния между точками ;3)
Слайд 2 Расстояние между точками А и В можно вычислить:
1) как
длину отрезка АВ, если отрезок АВ удается включить в некоторый треугольник в качестве одной из его сторон;
2) по формуле нахождения расстояния между точками ;
3) по формуле нахождения длины вектора.
2) по формуле нахождения расстояния между точками ;
3) по формуле нахождения длины вектора.
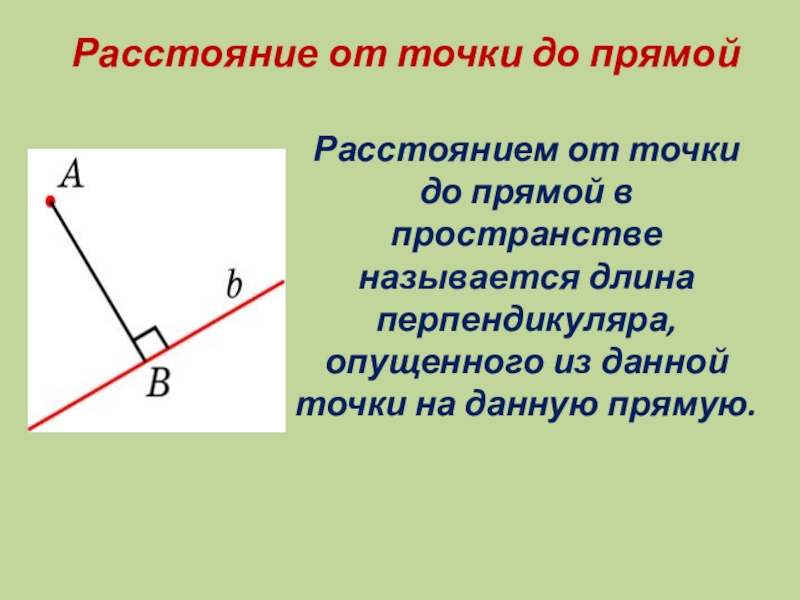
Слайд 3 Расстояние от точки до прямой
Расстоянием от точки до прямой
в пространстве называется длина перпендикуляра, опущенного из данной точки на данную прямую.
Слайд 4Расстояние от точки до прямой можно вычислить:
1) как длину отрезка
перпендикуляра, если удается включить этот отрезок в некоторый треугольник в качестве одной из высот;
2) используя векторный метод;
3) используя координатно-векторный метод.
2) используя векторный метод;
3) используя координатно-векторный метод.
Слайд 7Задачи для самостоятельного решения
1)В правильной треугольной призме
ABCA₁B₁C₁
, все ребра которой равны 1, найдите расстояние от точки А до прямой ВС ₁ . Ответ: √14/4.
2) В правильной шестиугольной призме
АВC DEFA₁B₁C₁D₁ E₁ F₁ A₁ , все ребра которой равны 1, найдите расстояние от точки А до прямой: а) DЕ;
б) D₁E₁ ; в) B₁C₁ ; г) BE₁ ; д) BC₁ ;
е) CE₁ ; ж) CF₁ ; з) CB₁ .
Ответ: а) √3; б) 2; в) √7/2 ; г) 2√5/5 ; д)√14/4 ; е) √2; ж) √30/5 ; з) √30/4 .
2) В правильной шестиугольной призме
АВC DEFA₁B₁C₁D₁ E₁ F₁ A₁ , все ребра которой равны 1, найдите расстояние от точки А до прямой: а) DЕ;
б) D₁E₁ ; в) B₁C₁ ; г) BE₁ ; д) BC₁ ;
е) CE₁ ; ж) CF₁ ; з) CB₁ .
Ответ: а) √3; б) 2; в) √7/2 ; г) 2√5/5 ; д)√14/4 ; е) √2; ж) √30/5 ; з) √30/4 .
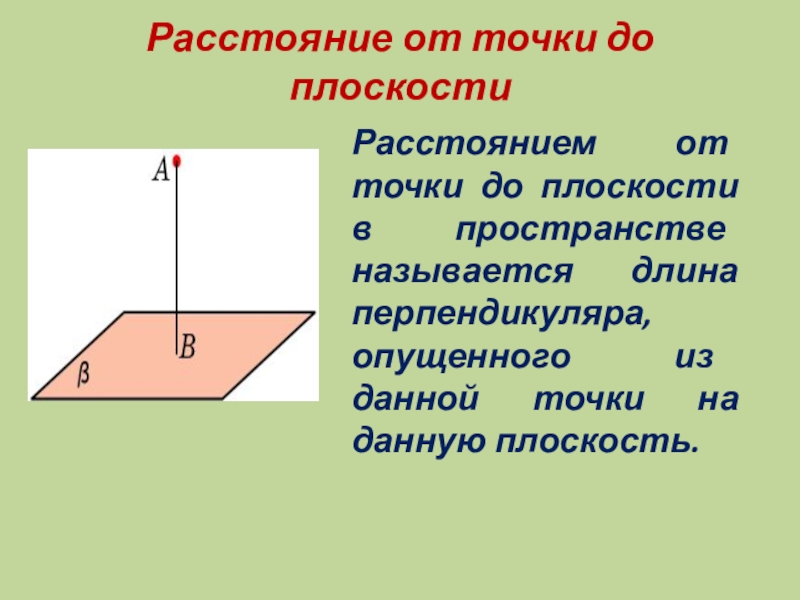
Слайд 8Расстояние от точки до плоскости
Расстоянием от точки до плоскости в пространстве
называется длина перпендикуляра, опущенного из данной точки на данную плоскость.
Слайд 9• Расстояние от точки до плоскости, не содержащей эту точку, есть
длина отрезка перпендикуляра, опущенного из этой точки на плоскость.
• Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
• Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
• Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
• Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
• Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
• Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
• Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
• Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
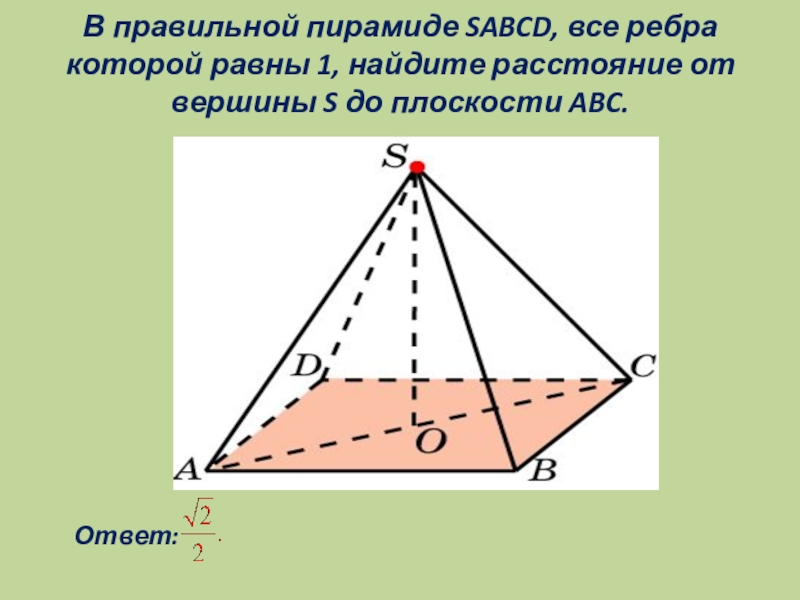
Слайд 11В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние
от вершины S до плоскости ABC.
Слайд 12Задачи для самостоятельного решения
1.В правильном тетраэдре ABCD найдите расстояние от вершины
D до плоскости ABC.
Ответ:√6/3
2.В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от вершины S до плоскости ABC.
Ответ:√3
3. В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние от точки A до плоскости CFF1.
Ответ: √3/3
4. В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние от точки A до плоскости BA1E1.
Ответ: √2/2
5.В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние от точки A до плоскости A1B1D.
Ответ: √3/2
Ответ:√6/3
2.В правильной 6-ой пирамиде SABCDEF, боковые ребра которой равны 2, а ребра основания – 1, найдите расстояние от вершины S до плоскости ABC.
Ответ:√3
3. В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние от точки A до плоскости CFF1.
Ответ: √3/3
4. В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние от точки A до плоскости BA1E1.
Ответ: √2/2
5.В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние от точки A до плоскости A1B1D.
Ответ: √3/2
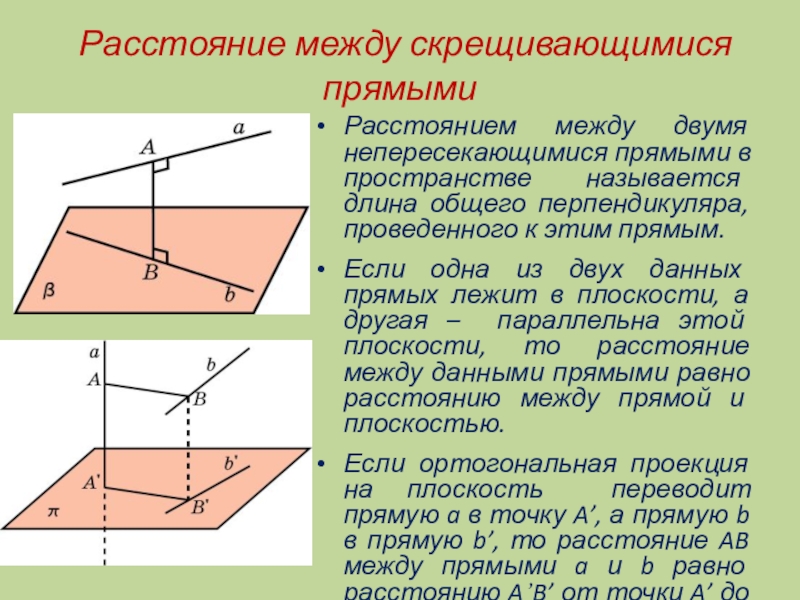
Слайд 13 Расстояние между скрещивающимися прямыми
Расстоянием между двумя непересекающимися прямыми в
пространстве называется длина общего перпендикуляра, проведенного к этим прямым.
Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.
Если ортогональная проекция на плоскость переводит прямую a в точку A’, а прямую b в прямую b’, то расстояние AB между прямыми a и b равно расстоянию A’B’ от точки A’ до прямой B’.
Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.
Если ортогональная проекция на плоскость переводит прямую a в точку A’, а прямую b в прямую b’, то расстояние AB между прямыми a и b равно расстоянию A’B’ от точки A’ до прямой B’.
Слайд 15В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние
между прямыми: AA1 и B1C1.
Ответ:√3/2
Слайд 16Задачи для самостоятельного решения
1.В правильной четырехугольной пирамиде SABCD, все ребра которой
равны 1, найдите расстояние между прямыми BD и SA.
Ответ: 0,5.
2.В пирамиде DABC известны длины ребер: 10,= = = = AB AC DB DC 12. = = BC DA Найдите расстояние между прямыми DA и ВС.
Ответ: 2√7
3.В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BC.
Ответ: √6/3
4. В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AВ и BE.
Ответ: √3
Ответ: 0,5.
2.В пирамиде DABC известны длины ребер: 10,= = = = AB AC DB DC 12. = = BC DA Найдите расстояние между прямыми DA и ВС.
Ответ: 2√7
3.В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BC.
Ответ: √6/3
4. В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AВ и BE.
Ответ: √3