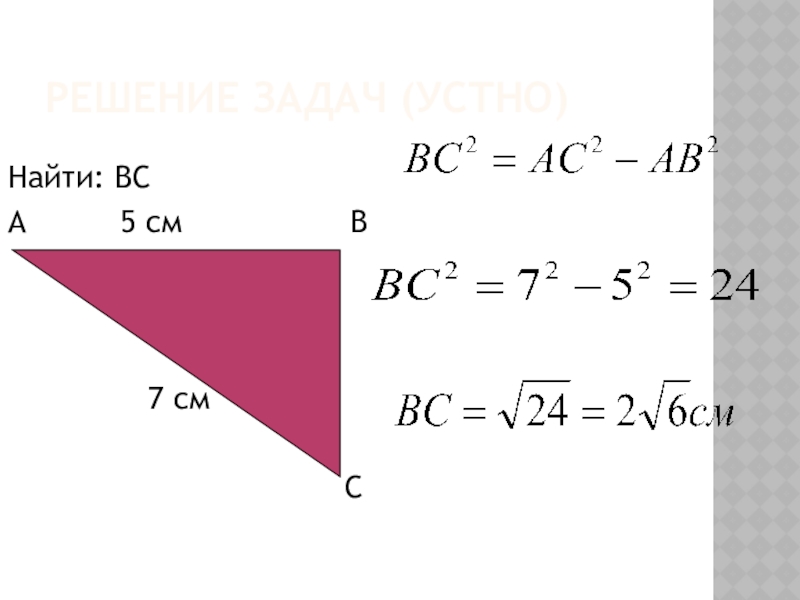- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии на тему; Теорема, обратная теореме Пифагора
Содержание
- 1. Презентация к уроку геометрии на тему; Теорема, обратная теореме Пифагора
- 2. Цели урока:Рассмотреть теорему, обратную теореме Пифагора;Рассмотреть применение
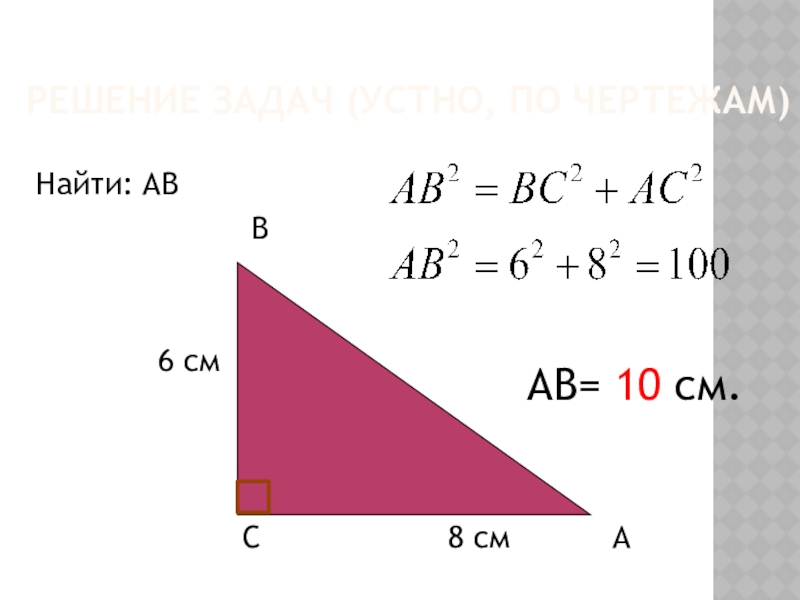
- 3. Решение задач (устно, по чертежам)Найти: АВ
- 4. Решение задач (устно)Найти: ВСА
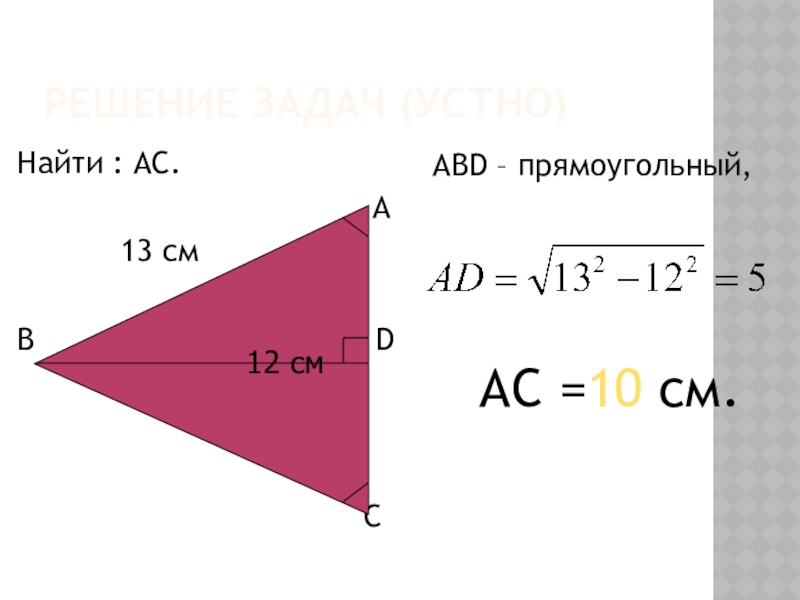
- 5. Решение задач (устно)Найти : АС.
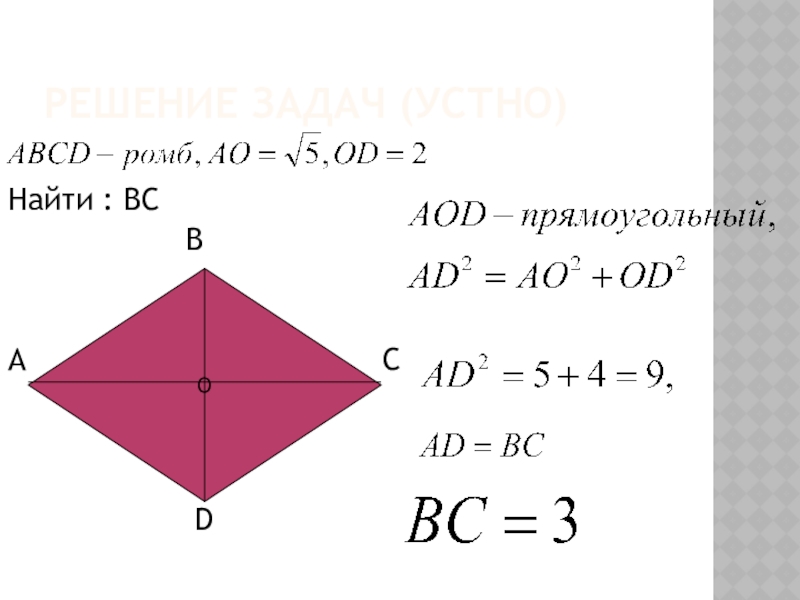
- 6. Решение задач (устно)Найти : ВС
- 7. Решение задач (устно)АВСD – прямоугольник, АВ:AD=3:4,Найти: АD.
- 8. Решение задач (устно)Найти : АВ.
- 9. Сформулируйте утверждения обратные данным и выясните ,верны
- 10. Сформулируйте утверждения обратные данным и выясните ,верны
- 11. Сформулируйте утверждения обратные данным и выясните ,верны
- 12. Если квадрат одной стороны треугольника
- 13. Прямоугольные треугольники, длины сторон которых выражаются целыми
- 14. Треугольник со сторонами3,4 и 5 был известен
- 15. Учебник (устно)№498 (а,б,в)Выясните является ли треугольник прямоугольным,
- 16. Учебник (письменно)№499 а)Найдите меньшую высоту треугольника, если
- 17. СамостоятельноОпределите углы треугольника со сторонами 1,1, В
- 18. Проверка1)2)3)
- 19. Итог урокаЧто нового вы узнали на сегодняшнем уроке?Кто лучше всех работал ?Что понравилось ?
- 20. Домашнее заданиеПункт 55;Вопросы 9,10;№498 (г, д,е)№499 (б)№488
- 21. Спасибо за внимание!
Цели урока:Рассмотреть теорему, обратную теореме Пифагора;Рассмотреть применение теоремы в процессе решения задач;Закрепить теорему Пифагора и совершенствовать навыки решения задач на ее применение.
Слайд 2Цели урока:
Рассмотреть теорему, обратную теореме Пифагора;
Рассмотреть применение теоремы в процессе решения
задач;
Закрепить теорему Пифагора и совершенствовать навыки решения задач на ее применение.
Закрепить теорему Пифагора и совершенствовать навыки решения задач на ее применение.
Слайд 9Сформулируйте утверждения обратные данным и выясните ,верны ли они:
Сумма смежных углов
равна 180 градусам;
Если сумма двух углов равна 180 градусам, то они смежные;
НЕ ВЕРНО!
Диагонали ромба взаимно перпендикулярны
Если диагонали четырехугольника взаимно перпендикулярны, то он – ромб;
НЕ ВЕРНО!
Если сумма двух углов равна 180 градусам, то они смежные;
НЕ ВЕРНО!
Диагонали ромба взаимно перпендикулярны
Если диагонали четырехугольника взаимно перпендикулярны, то он – ромб;
НЕ ВЕРНО!
Слайд 10Сформулируйте утверждения обратные данным и выясните ,верны ли они:
Вертикальные углы равны;
Если
углы равны, то они вертикальные;
НЕ ВЕРНО!
В параллелограмме противолежащие стороны равны;
Если в четырехугольнике противолежащие стороны равны, то он – параллелограмм;
НЕ ВЕРНО!
НЕ ВЕРНО!
В параллелограмме противолежащие стороны равны;
Если в четырехугольнике противолежащие стороны равны, то он – параллелограмм;
НЕ ВЕРНО!
Слайд 11Сформулируйте утверждения обратные данным и выясните ,верны ли они:
В прямоугольном треугольнике
квадрат гипотенузы, равен сумме квадратов катетов
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный
Слайд 12 Если квадрат одной стороны треугольника равен сумме квадратов двух
других сторон, то треугольник прямоугольный.
Данное утверждение называют теоремой, обратной теореме Пифагора.
Данное утверждение называют теоремой, обратной теореме Пифагора.
Слайд 13Прямоугольные треугольники, длины сторон которых выражаются целыми числами, называются
Пифагоровыми треугольниками.
Например: 26,
24 и 10
-Приведите примеры Пифагоровых треугольников
10,8 и 15; 13,12 и 5; 5,4 и 3; 15,12 и 9 и т.д.
-Являются ли Пифагоровыми треугольниками треугольники: а) с гипотенузой 25 и катетом 15;
б) с катетами 5 и 4?
-Приведите примеры Пифагоровых треугольников
10,8 и 15; 13,12 и 5; 5,4 и 3; 15,12 и 9 и т.д.
-Являются ли Пифагоровыми треугольниками треугольники: а) с гипотенузой 25 и катетом 15;
б) с катетами 5 и 4?
Слайд 14Треугольник со сторонами
3,4 и 5 был известен еще
древним египтянам. Египтяне
использовали их
для построе-
ния прямых углов. Делали они
это так: на веревке делали
метки, делящие ее на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3,4 и 5. Угол лежащий против стороны, равной 5, оказывался прямым. Этот треугольник получил название египетского треугольника и по сей день именно так его и называют
ния прямых углов. Делали они
это так: на веревке делали
метки, делящие ее на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3,4 и 5. Угол лежащий против стороны, равной 5, оказывался прямым. Этот треугольник получил название египетского треугольника и по сей день именно так его и называют
Слайд 15Учебник (устно)
№498 (а,б,в)
Выясните является ли треугольник прямоугольным, если его стороны выражаются
числами:
а) 6,8 и 10
36+64=100, 100=100 Является
б)5,6 и 7
25+36=61, 61≠ 49 Не является
в)9,12 и 15
81+144=225,225=225 Является
а) 6,8 и 10
36+64=100, 100=100 Является
б)5,6 и 7
25+36=61, 61≠ 49 Не является
в)9,12 и 15
81+144=225,225=225 Является
Слайд 16Учебник (письменно)
№499 а)
Найдите меньшую высоту треугольника, если его стороны равны:
а)
24 см, 25 см, 7 см.
Решение:
; 625=576+49=625, значит треугольник прямоугольный и его S равна половине произведения его катетов, т.е. S=0,5*24*7=84.
Меньшая высота проведена к большей стороне, а в прямоугольном треугольнике большая сторона – гипотенуза, то h=(2S)/25 , h=2*84:25=6,72 (см).
Ответ: 6,72 см.
Решение:
; 625=576+49=625, значит треугольник прямоугольный и его S равна половине произведения его катетов, т.е. S=0,5*24*7=84.
Меньшая высота проведена к большей стороне, а в прямоугольном треугольнике большая сторона – гипотенуза, то h=(2S)/25 , h=2*84:25=6,72 (см).
Ответ: 6,72 см.
Слайд 17Самостоятельно
Определите углы треугольника со сторонами 1,1,
В треугольнике АВС АВ=
, ВС=2. На стороне АС отмечена точка М так, что АМ=1, ВМ=1. Найдите АС.
В треугольнике МРК РК=2. На стороне МК отмечена точка А так, что МА=АР= , АК=1. Найдите угол МРК.
В треугольнике МРК РК=2. На стороне МК отмечена точка А так, что МА=АР= , АК=1. Найдите угол МРК.
Слайд 19Итог урока
Что нового вы узнали на сегодняшнем уроке?
Кто лучше всех работал
?
Что понравилось ?
Что понравилось ?