- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии на тему Векторы в пространстве (11 класс)
Содержание
- 1. Презентация к уроку геометрии на тему Векторы в пространстве (11 класс)
- 2. СодержаниеПонятиеПонятие вектораРавенство векторовСложение и вычитание векторовСумма нескольких
- 3. Понятие вектораОтрезок, для которого указано, какой из
- 4. Длина вектораДлиной ненулевого вектора АВ называется длина
- 5. Два ненулевых вектора называются коллинеарными ,если они
- 6. Равенство векторовВекторы называются равными, если они соноправлены
- 7. От любой точки можно отложить вектор, равный
- 8. Сложение и вычитание векторовПравило треугольника.Для любых трех
- 9. Свойства сложения векторов.Для любых векторов а, b,
- 10. Два ненулевых вектора называются противоположными, если их
- 11. Разностью векторов а и b называется такой
- 12. Сумма нескольких векторовСумма нескольких векторов не зависит
- 13. Умножение вектора на числоПроизведением ненулевого вектора а
- 14. Компланарные векторыВекторы называются компланарными, если при откладывании
- 15. Признак копланарности трех векторовЕсли вектор с можно
- 16. Правило параллелепипедаПусть а, b, с – некомпланарные
- 17. Разложение по трем некомпланарным векторамЕсли вектор р
- 18. Математический диктантНарисуйте параллелепипед АВСDA1В1С1D1.Найдите вектор, начало и
- 19. Контрольный тест1.Дан параллелепипед АВСDA1В1С1D1. Укажите вектор с
- 20. Слайд 20
Слайд 2Содержание
ПонятиеПонятие вектора
Равенство векторов
Сложение и вычитание векторов
Сумма нескольких векторов
Умножение вектора на число
Компланарные
Правило параллелепипеда
Разложение вектора по трем некомпланарным векторам
Математический диктант
Контрольный тест
Слайд 3Понятие вектора
Отрезок, для которого указано, какой из его концов считается началом,
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым.
ТТ – нулевой вектор ( ТТ = О)
А
В
С
D
T
Слайд 4Длина вектора
Длиной ненулевого вектора АВ называется длина отрезка АВ.
Длина вектора АВ(вектора
Длина нулевого вектора считается равной нулю: 0 =0
А
В
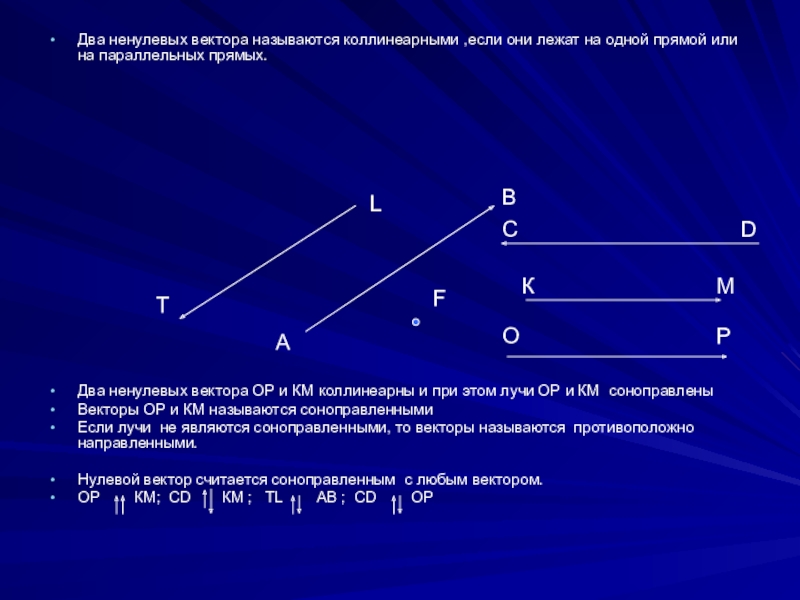
Слайд 5Два ненулевых вектора называются коллинеарными ,если они лежат на одной прямой
Два ненулевых вектора ОР и КМ коллинеарны и при этом лучи ОР и КМ соноправлены
Векторы ОР и КМ называются соноправленными
Если лучи не являются соноправленными, то векторы называются противоположно направленными.
Нулевой вектор считается соноправленным с любым вектором.
ОР КМ; CD КМ ; TL AB ; CD OP
А
В
С
D
К
М
F
L
T
O
P
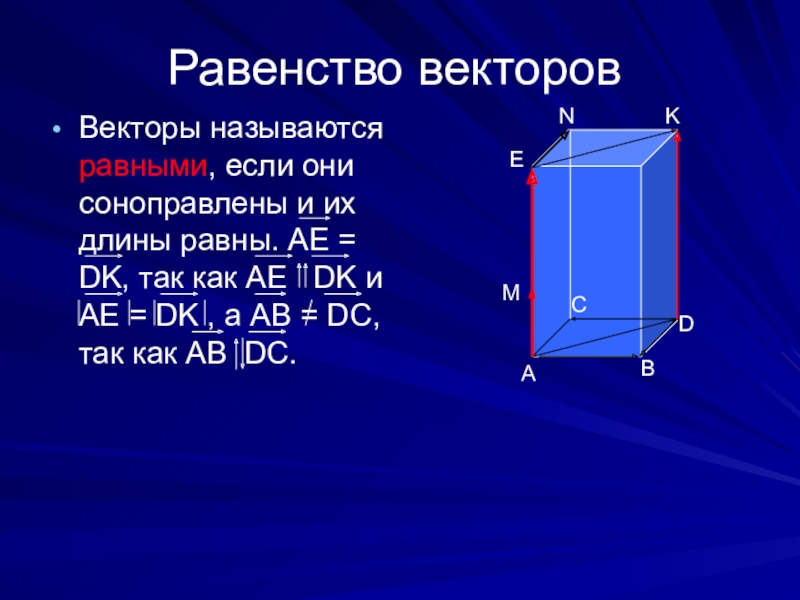
Слайд 6Равенство векторов
Векторы называются равными, если они соноправлены и их длины равны.
A
B
D
N
K
E
C
M
Слайд 7От любой точки можно отложить вектор, равный данному, и притом только
Доказательство. В самом деле, пусть а – данный вектор, М – данная точка. Проведем через начало и конец вектора а и точку М плоскость и в этой плоскости построим вектор MN = a. Очевидно, что вектор MN искомый. Из построения ясно также, что MN – единственный вектор с началом М, равный вектору а.
а
М
N
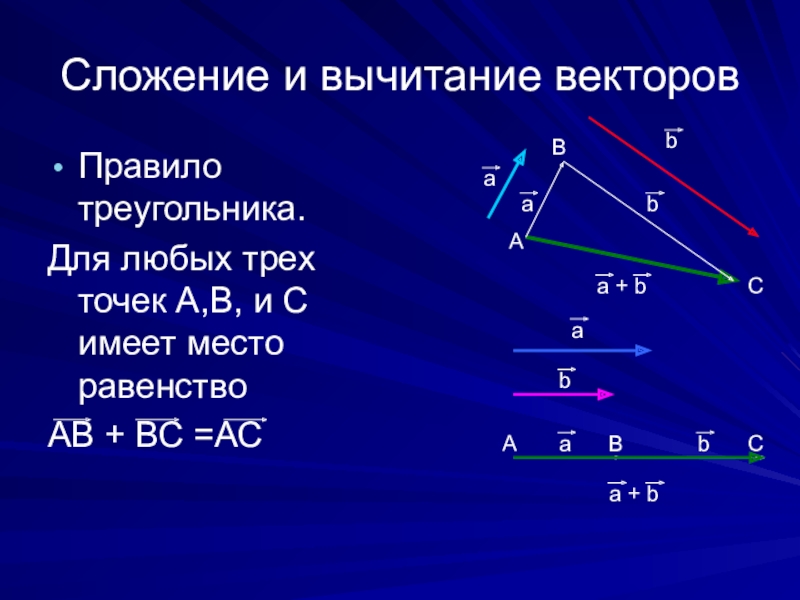
Слайд 8Сложение и вычитание векторов
Правило треугольника.
Для любых трех точек А,В, и С
АВ + ВС =АС
А
С
В
а
а
b
b
a + b
а
b
A
C
B
a
b
a + b
Слайд 9Свойства сложения векторов.
Для любых векторов а, b, с справедливы равенства:
1) а
2) ( а+b ) + c = a + ( b + c ) ( cочетательный закон )
Правило параллелограмма сложения двух неколлинеарных векторов
а
а + в
b
a
b
Слайд 10Два ненулевых вектора называются противоположными, если их длины равны и они
АВ и ВА - противоположные векторы
А
В
Слайд 11Разностью векторов а и b называется такой вектор, сумма которого с
Разность а - b векторов а и b можно найти по формуле а - b = a + (-b) , где
(-b) – вектор, противоположный вектору b.
а
b
- b
а - b
а
В
А
О
А
О
В
а
b
а - b
Слайд 12Сумма нескольких векторов
Сумма нескольких векторов не зависит от того, в каком
Правило многоугольника.
Если А1 , А2, …, Аn - произвольные точки, то А1А2 + А2А3+…+Аn-1Аn = А1Аn
OC = a + b + c
O
C
A
B
a
b
c
Слайд 13Умножение вектора на число
Произведением ненулевого вектора а на число к называется
Если а = 0, то b = 0.
Если к = 0, то b = 0.
Основные свойства
(kl)a = k(la) сочетательный закон
k( a + b ) = ka + kb I распределительный закон
( k + l )a = ka + la II распределительный закон
Если а и b коллинеарны и а = о, то существует к, что b=ka.
Слайд 14Компланарные векторы
Векторы называются компланарными, если при откладывании их от одной и
На рисунке векторы ВВ1, ОD и ОЕ компланарны, так как если отложить от точки О вектор, равный ВВ1 , то получится вектор ОС, а векторы ОС, ОD и ОЕ лежат в одной плоскости ОСЕ. Векторы ОА, ОВ и ОС не компланарны, так как вектор ОС не лежит в плоскости ОАВ.
а
b
c
B1
D
C
B
O
A
E
Слайд 15Признак копланарности трех векторов
Если вектор с можно разложить по векторам а
Доказательство.
Будем считать, что векторы а и b не коллинеарны. Отложим от произвольной точки О векторы ОА=а и ОВ= b. Векторы ОА и ОВ лежат в плоскости ОАВ. Очевидно, в этой же плоскости лежат векторы ОА1=х*ОА и ОВ1=у*ОВ, а следовательно, и их сумма – вектор ОС= х*ОА + у*ОВ, равный вектору с. Итак, векторы ОА=а, ОВ= b и ОС=с лежат в одной плоскости, т.е. векторы а, b и с компланарны.
Справедливо и обратное утверждение : если векторы а,
b и с компланарны, а векторы а и b не коллинеарны, то вектор с можно разложить по векторам а и b, причем коэффициенты разложения определяются единственным образом.
В1
А1
С
а
b
ОА1=х*ОА
ОВ1=у*ОВ
ОС= х*ОА + у*ОВ
В
А
Слайд 16Правило параллелепипеда
Пусть а, b, с – некомпланарные векторы. Отложим от произвольной
а
b
B1
C
B
O
E
D
c
A
Слайд 17Разложение по трем некомпланарным векторам
Если вектор р представлен в виде
Теорема.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Доказательство.
Пусть а, b и с – данные некомпланарные векторы. Докажем сначала, что любой вектор р можно представить в виде р = ха + уb + zc.
Отметим произвольную точку о и отложим от этой точки векторы:
ОА=а, ОВ=b, OC=c, OP=p.
Через точку Р проведем прямую, параллельную прямой ОС, и обозначим через точку Р1 точку пересечения этой прямой с плоскостью АОВ. Затем через точку Р1 проведем прямую, параллельную прямой ОВ, и обозначим через точку Р2 точку пересечения этой прямой с прямой ОА.
По правилу многоугольника ОР = ОР2 + Р2 Р1 + Р1Р.
Векторы ОР2 и ОА, Р2 Р1 и ОВ, Р1Р и ОС коллинеарны, поэтому существуют числа х,у и z такие, что
ОР2 = х* ОА, Р2 Р1 = у*ОВ, Р1Р= z* OC. Подставив эти выражения в равенство ОР = ОР2 + Р2 Р1 + Р1Р, получим ОР = х* ОА + у*ОВ + z* OC. Отсюда, учитывая равенства
ОА=а, ОВ=b, OC=c, OP=p, приходим к р = ха + уb + zc.
Докажем теперь, что коэффициенты разложения в формуле определяются единственным образом. Допустим, что наряду с разложением имеется и другое разложение вектора р: р – х1а + у1b + z1c. Вычитая это равенство из равенства р = ха + уb + zc и используя свойства действий над векторами, получаем : 0 = (х - х1 )а + (у - у1)b + ( z - z1)c. Это равенство выполняется только тогда, когда х - х1 = 0, у - у1 =0, z - z1 = 0. Коэффициенты разложения определяются единственным способом. Теорема доказана.
С
с
О
Р
р
В
Р2
а
А
b
P1
Слайд 18Математический диктант
Нарисуйте параллелепипед АВСDA1В1С1D1.
Найдите вектор, начало и конец которого являются вершинами
Найдите вектор, равный: а) АD - С1D1 - ВВ1 ; б) АВ - АA1 - С1В1
Представьте вектор ВС1 в виде разности двух векторов, один из которых вектор ВD1; вектор D1В.
Упростите выражение: а) MN – PQ – NM + RQ + TR; б) LP + MS + EN – MN – PL + ST
Упростите выражение: а) 3( a + b ) – 4( 2a – b ) + a; б) m + 3( 2m – n) – 2( m – 4n)
Слайд 19Контрольный тест
1.Дан параллелепипед АВСDA1В1С1D1. Укажите вектор с началом и концом в
а) A1В1 + ВС + DD1 + СD а) В1С +АВ +ВВ1 + В1А
б) АВ - СС1 б) DС - ВВ1
2. Дан тетраэдр DАВС. Точка М – середина ребра ВС, точка N - середина отрезка DМ. Выразите вектор AN через вектора а=АВ, b=АС и с=AD ( I вариант)
Дан тетраэдр DАВС. Медианы треугольника BDC пересекаются в точке Р,К – середина отрезка АР. Выразите вектор ВК через векторы а=АВ, b=Ас и с=AD (II вариант).
3. В параллелепипеде АВСDA1В1С1D1 медианы треугольника АВD пересекаются в точке Р. Разложите вектор В1Р по векторам а = В1А, b = В1С, c = В1В (I вариант).
В параллелепипеде АВСDA1В1С1D1 точка О лежит на отрезке В1D1, причем В1О : ОD1 = 2 :1. Разложите вектор АО по векторам а=АВ1 , b = АD1, c= A1А (II вариант).