- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии на тему: Осевая и центральная симметрии (8 класс)
Содержание
- 1. Презентация к уроку геометрии на тему: Осевая и центральная симметрии (8 класс)
- 2. В древности слово «СИММЕТРИЯ» употреблялось
- 3. Осевая симметрия Точки А и А1
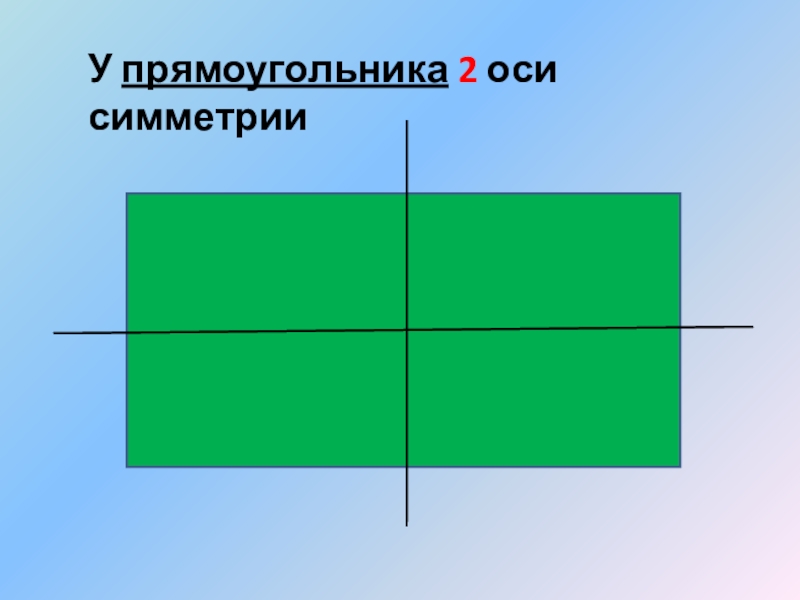
- 4. У прямоугольника 2 оси симметрии
- 5. А вот у круга бесконечно много осей симметрии, все они являются диаметрами
- 6. У геометрических фигур может быть одна или
- 7. У геометрических фигур может быть одна или
- 8. Центральная симметрия Точки А1 и А2 называются
- 9. Центральная симметрия А В СА1С1АВСОС1А1В1
- 10. Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм Параллелограмм ОкружностьоО
- 11. Фигуры, обладающие центральной и осевой симметриейОВАLNDСФигура называется
- 12. Практическая работа Определить фигуры: обладающие
- 13. Слайд 13
- 14. Домашнее задание:п.47; № 421, 423
В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота». В переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей».
Слайд 2 В древности слово «СИММЕТРИЯ» употреблялось в значении «гармония», «красота».
В переводе с греческого это слово означает «соразмерность, пропорциональность, одинаковость в расположении частей».
Слайд 3Осевая симметрия
Точки А и А1 называются симметричными относительно прямой
а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
а
А
А1
а – ось симметрии
Р
М
М1
b
N
N1
Точка Р симметрична самой себе
относительно прямой b
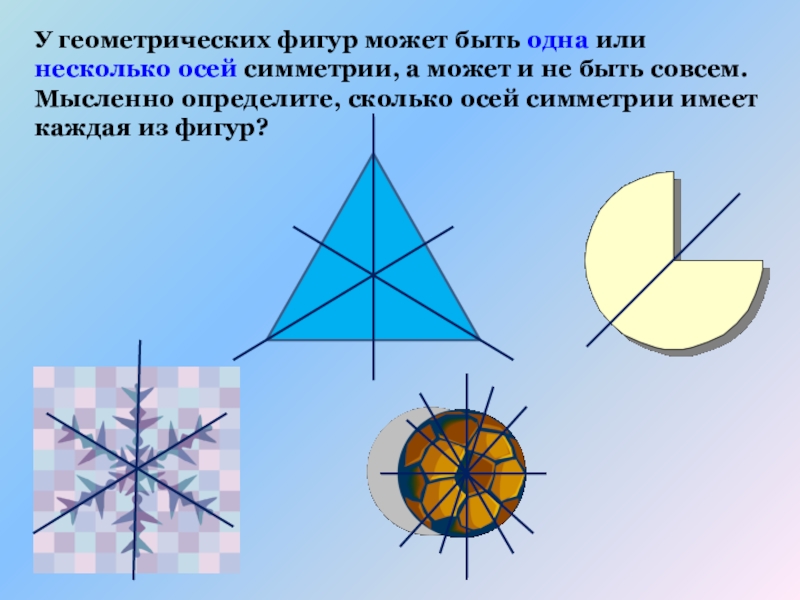
Слайд 6У геометрических фигур может быть одна или несколько осей симметрии, а
может и не быть совсем.
Мысленно определите, сколько осей симметрии имеет каждая из фигур?
Слайд 7У геометрических фигур может быть одна или несколько осей симметрии, а
может и не быть совсем.
Мысленно определите, сколько осей симметрии имеет каждая из фигур?
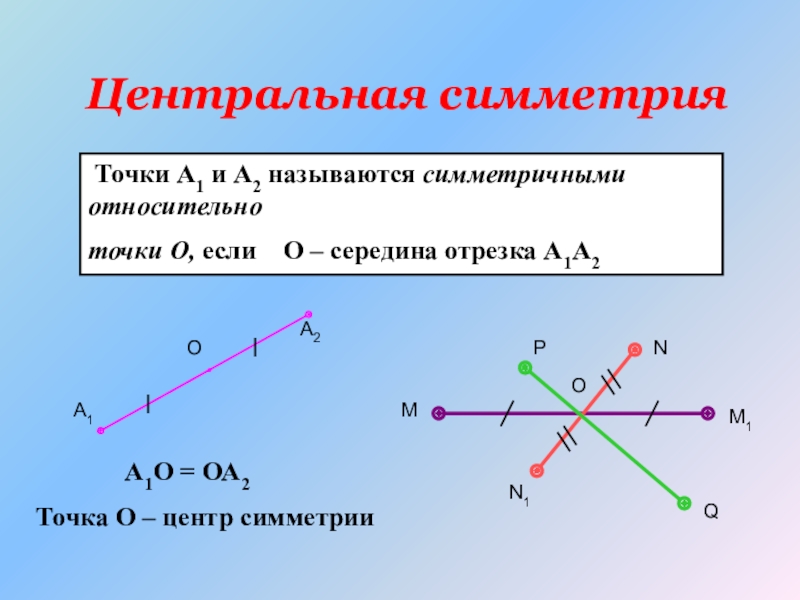
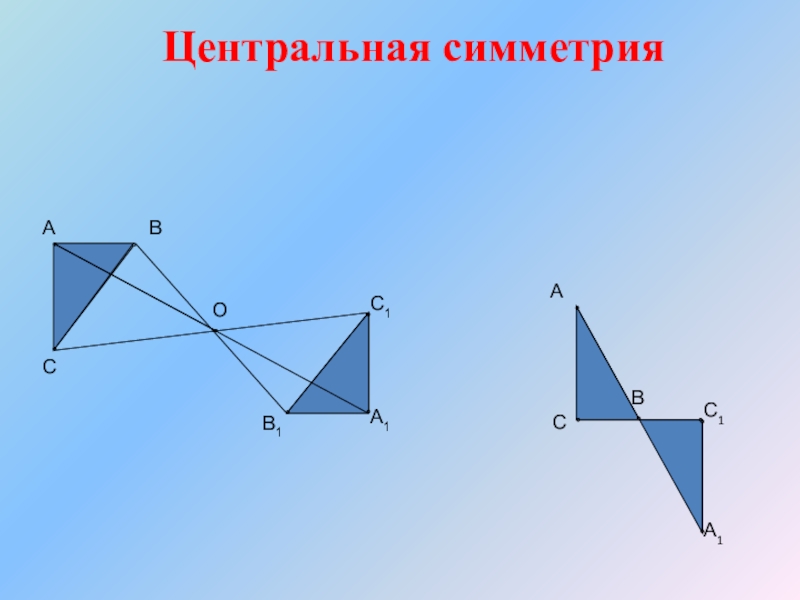
Слайд 8Центральная симметрия
Точки А1 и А2 называются симметричными относительно
точки О,
если О – середина отрезка А1А2
А1
А2
О
О
Р
Q
M
M1
N
N1
А1О = ОА2
Точка О – центр симметрии
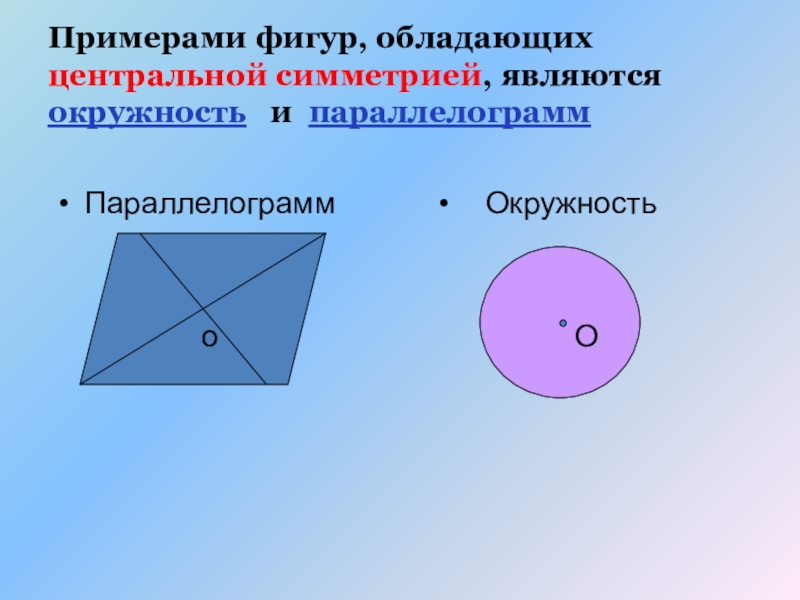
Слайд 10Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм
Параллелограмм
Окружность
о
О
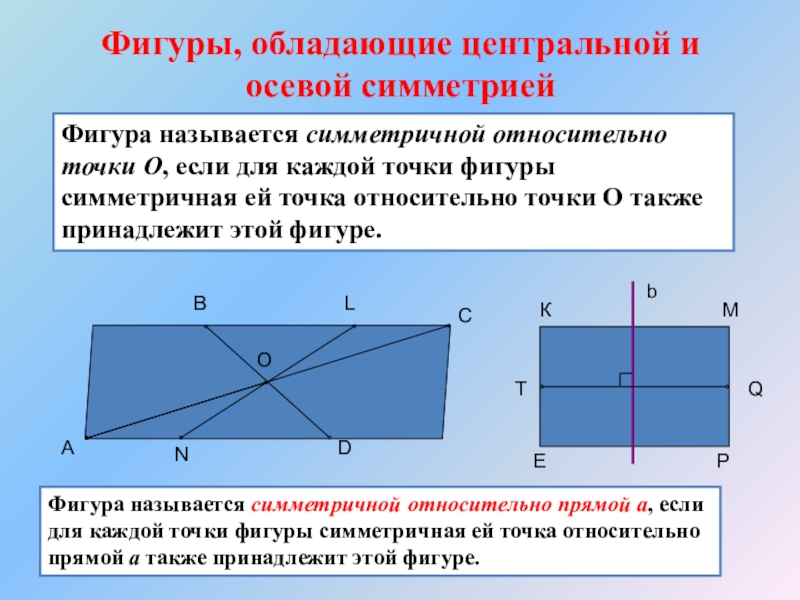
Слайд 11Фигуры, обладающие центральной и осевой симметрией
О
В
А
L
N
D
С
Фигура называется симметричной относительно точки О,
если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре.
К
М
E
P
b
T
Q
Слайд 12
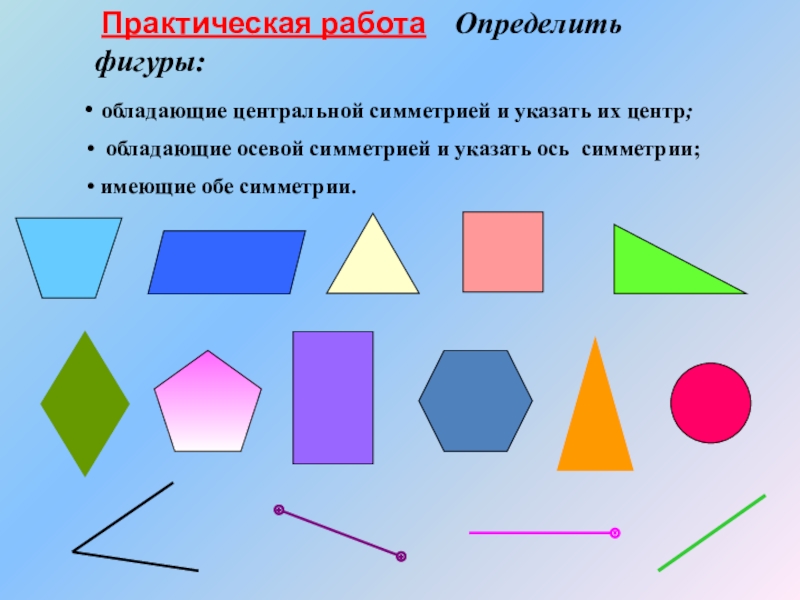
Практическая работа Определить фигуры:
обладающие центральной симметрией и указать
их центр;
обладающие осевой симметрией и указать ось симметрии;
имеющие обе симметрии.
обладающие осевой симметрией и указать ось симметрии;
имеющие обе симметрии.
