- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии, Л.С. Атанасян, 8 класс Центральные и вписанные углы
Содержание
- 1. Презентация к уроку геометрии, Л.С. Атанасян, 8 класс Центральные и вписанные углы
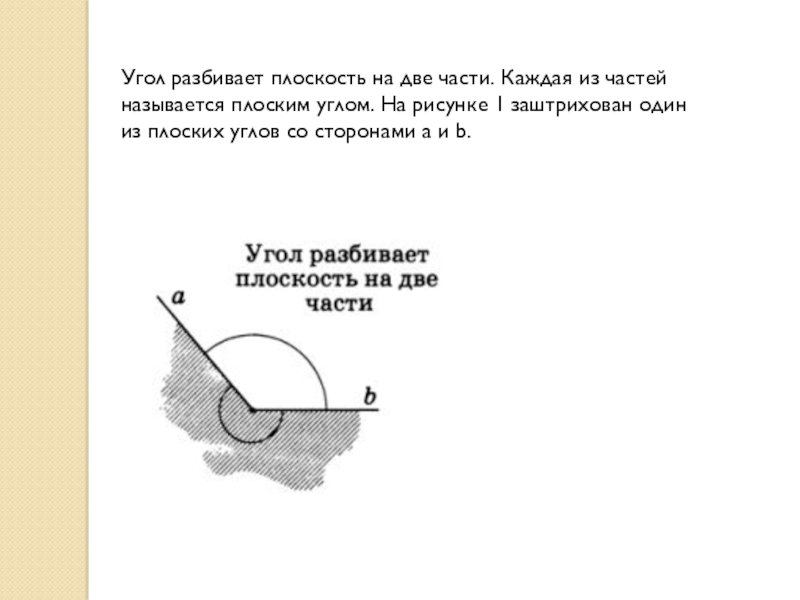
- 2. Угол разбивает плоскость на две части. Каждая
- 3. Плоские
- 4. Центральным
- 5. Угол, вершина которого лежит на окружности,
- 6. Теорема 1. Угол, вписанный в окружность, равен
- 7. Пример 1. Точки А, В, С лежат
- 8. Пример 2. Точки А, В, С лежат
- 9. Следствие 1. Вписанные углы, стороны которых проходят
Слайд 2Угол разбивает плоскость на две части. Каждая из частей называется плоским
Слайд 3 Плоские углы с общими сторонами называются дополнительными. Если плоский
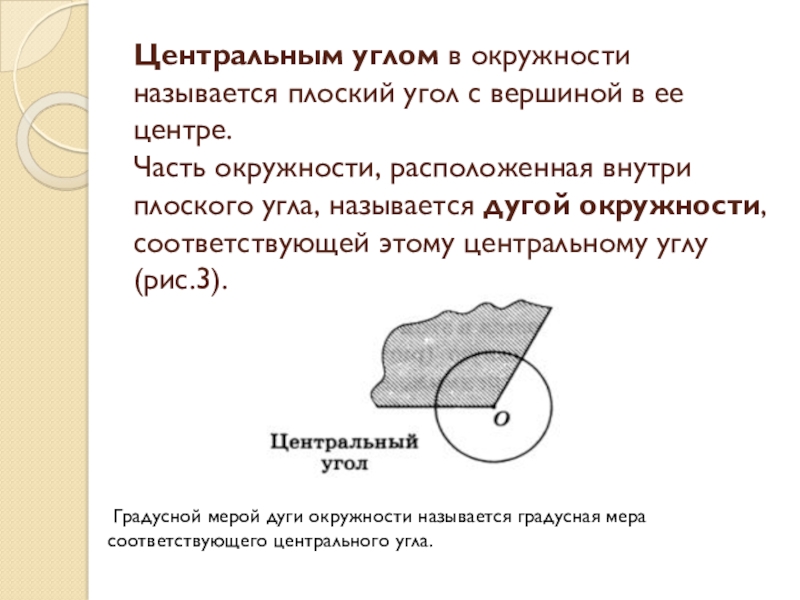
Слайд 4 Центральным углом в окружности называется плоский угол с вершиной в
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Слайд 5 Угол, вершина которого лежит на окружности,
а стороны пересекают эту
вписанным в окружность.
Угол ВАС на рисунке 4 вписан в окружность.
Его вершина А лежит на окружности, а стороны пересекают окружность в точках В и С. Говорят также, что угол А опирается на хорду ВС.
Прямая ВС разбивает окружность на две дуги. Центральный угол, соответствующий той из этих дуг, которая не содержит точку А, называется центральным углом, соответствующим данному вписанному углу.
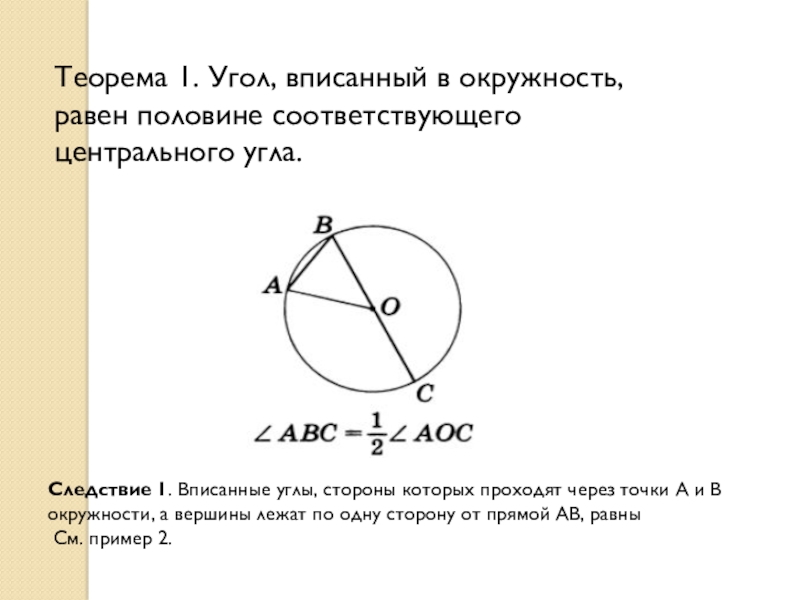
Слайд 6Теорема 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 1. Вписанные углы, стороны которых проходят через точки А и В окружности, а вершины лежат по одну сторону от прямой АВ, равны
См. пример 2.
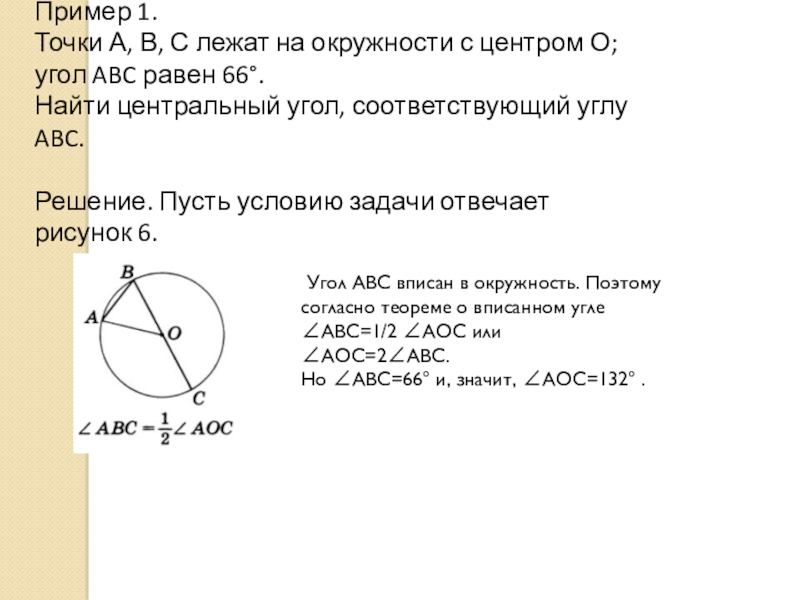
Слайд 7Пример 1.
Точки А, В, С лежат на окружности с центром
угол ABC равен 66°.
Найти центральный угол, соответствующий углу ABC.
Решение. Пусть условию задачи отвечает рисунок 6.
Угол ABC вписан в окружность. Поэтому согласно теореме о вписанном угле ∠ABC=1/2 ∠АОС или
∠АОС=2∠ABC.
Но ∠ABC=66° и, значит, ∠АОС=132° .
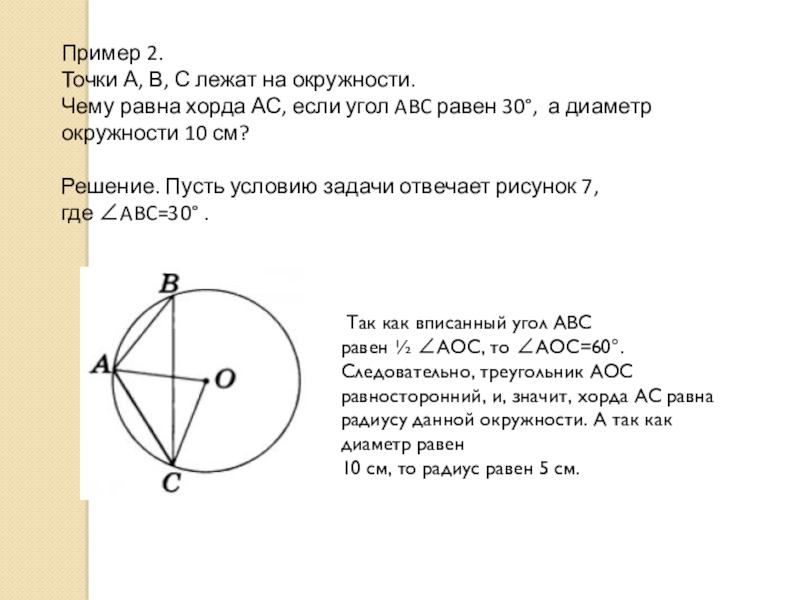
Слайд 8Пример 2.
Точки А, В, С лежат на окружности.
Чему равна
Решение. Пусть условию задачи отвечает рисунок 7,
где ∠ABC=30° .
Так как вписанный угол ABC
равен ½ ∠АОС, то ∠АОС=60°. Следовательно, треугольник АОС равносторонний, и, значит, хорда АС равна радиусу данной окружности. А так как диаметр равен
10 см, то радиус равен 5 см.
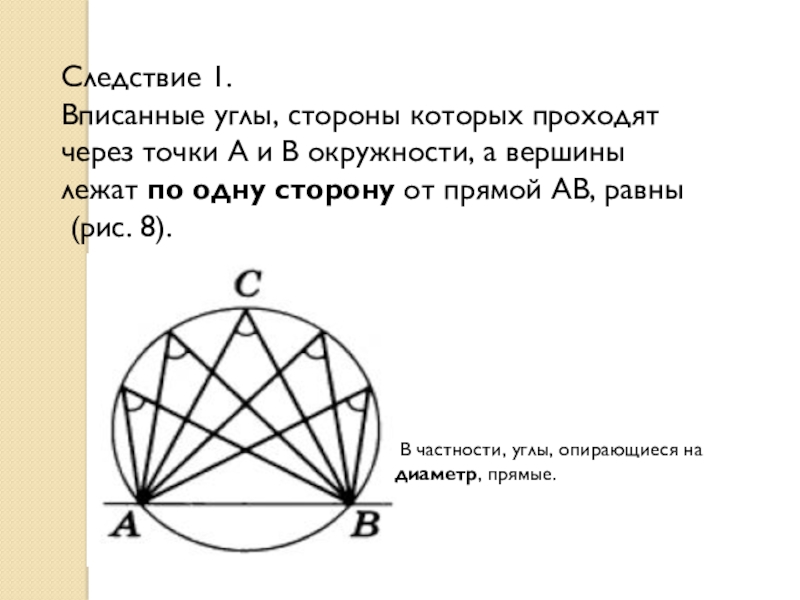
Слайд 9Следствие 1.
Вписанные углы, стороны которых проходят через точки А и
(рис. 8).
В частности, углы, опирающиеся на диаметр, прямые.